---

ガリレオ･ガイレイ Galileo Glilei(1564-1642)
 ピサ生まれ(ミケランジェロの死の三日前)の物理学者、天文学者。ピサ大学で医学を学ぶうち、ピサの聖堂内につるした燈の運動にヒントを得て振り子の等時性を発見。１９歳でユークリッド幾何学を学び、数学、物理学の研究に専念した。1589年ピサの斜塔で落体実験を行い、アリストテレスの学説の誤りを実証した。
  1592年パドパ大学数学教授。1604年落体の法則を発見し、1609年これを定式化した。また同年ガリレオ式望遠鏡を制作し、木星の衛星、太陽の黒点の発見をはじめ天体に関する新事実を発見し、コペルニクスの地動説の正しさを立証した。1610年フィレンツェに移り研究を続けたが、研究成果に対する反対派が多く、ローマに赴き弁明したが、1616年宗教裁判にかけられ地動説の放棄を命ぜられた。1632年に「二大体系対話」、1636年に「新科学対話」を著したが、その間幾多の迫害を受けた。

ガリレイの落下についての考え
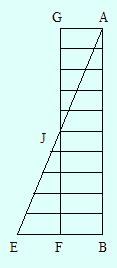
ガリレイは大気の抵抗を考えにいれると、物体が同じ速さで落下するということを「他（ピサ大学)の教授や哲学者それに全学生団の前で、ピサの斜塔のてっぺんから繰り返し行った実験によって」立証した。彼は＜新科学対話＞の中で、 「しかし、シンプリチオ君、私はこの実験で双方を200腕尺（43〜 53cm）の高さから落としたら、100または200ポンド(45.90Kg)あるいはそれ以上に重い砲丸も、僅か半ポンド(約227g)の重さしかないマスケット銃弾より、一スパンほども先に地面に達することはないと確信できる」としている。彼の大きな業績は、実験をしたことにあるが、それだけでなく、＜新科学対話＞では、多くの演繹的推論が含まれる。たとえば等加速運動を論議する際、速度は通過距離に比例するか？に対しては、「もしもある物体の４ヤード（約3.6m)の距離を通過する速度が、最初の2ヤード（約1.8m)を通過したときの速度の倍ならば、いずれの所要時間も等しくなければならない。しかし、4ヤードの通過が、2ヤードの通過と同一時間で行われるは、そこにInstaneous motionがあるときに限る。物体が落下する際には、時間がかかるので、実際には2ヤードの通過の方が、4ヤードの場合よりも、時間が少ないことがわかる。したがって、速度が落下距離に比例して増大するというのは真でない。」　ガリレイは、それから第2の仮定−速度は時間に比例する−へと進んだ。12ヤード（約11m）の板に幅1インチ（約2.5cm)の細長い溝を一直線にくりぬき、滑らかな羊皮紙でその上を覆った。この板を傾けてできる斜面の上に、完全に丸く、よく磨かれた真鍮の球を転がした。100回の実験の結果降下距離は常にほぼ時間の2乗に比例して変わることが認められた。この実験で時間の測定は水桶の水量の変化から調べた。ガリレイは、速度と距離の関係を示すために、＜静止状態から一様な速度で運動する物体が、所定の距離を通過する時間は同一距離を、終速度の半分の一様な速度で通過するに必要な時間に等しい＞という法則を確立した。図の線分EBは、ABの示す時間とともに、直接変化する終速度である。FBは平均速度、面積ABE＝面積ABFGで、通過距離を表している。
  水平投射の運動については、＜新科学対話＞の中で「誠にこの考えは新しく巧妙で鋭い。この考えは次の仮定に基づいている。横軸の運動が一定であり、それと同時に自然の加速による（垂直落下）運動も、時間の２乗に比例して、その（下方への）運動を続ける。この２つの運動は入り交じるが、お互いの運動を乱したり、変化させたりしないので、結局、前出運動が続けられ、＜projectile＞の軌道はくずれることがない････がこの振る舞いは、私にはとんと理解できない」と、サグレドにいわせている。

ガリレイの慣性の法則
ガリレイによって、加速度という概念の意義が認識された。ガリレイ以前は、物体に働く力は速度を決定すると考えられ、加速度の意義は考えれらてなかった。ガリレイの結果は一定の重力のもとで加速度が一定であることを示しており、これは、力は加速度を決めることを暗示する。
慣性を認識しはっきり述べたのもガリレイであった。＜新科学対話＞について次のように述べられている。ABの斜面を転がり降りた玉は、抵抗力を無視すればもとの高さまで昇る。θ＝０の場合無限まで走り続ける。図に示すように、一つの完全になめらかな斜面に沿って球を転がし落とす。この球がそのまま他の斜面に沿って上がっていくなら、最初の高さhと同じ高さまで到達するであろう。だから、上がる斜面の傾きをだんだん小さくしていればどうなるだろうか。到達距離はどんどん増して、ついにθ→0になった極限を考えれば、球は無限の彼方まで運動し続けることになる。これは「慣性の法則」のもとになる考えである。
ガリレイは、慣性の法則を水平面上でのみ成り立つと考えており、現在知られている「慣性の法則」にまで定式化するまでは至ってなかった。いずれにせよ、運動の変化の原因が物体外におかれた点は特記するべきことである。
      　　　　　　　　　      　　　　　　　　　      　　　　　　　　　      　　　　　　　　　      　　　　　　　　　      　　　　　　　　　      　　　　　　　　

戻る 

---

ヨハネス･ケプラー(Johannes Kepler1571-1630)
 ビュルテルベルグで生まれた天文学者。病弱だったため、牧師にしか向いていないと見られ、宗教的訓練を受ける。はじめはチュービンゲン大学で神学を学んだが、後に数学、天文学に転じた。
1593年　オーストリアのグラーツ州立学校に数学と天文学の教師として赴任。
1594年からグラーツ大学で数学、天文学を教えた。そのかたわら暦を占星術で作った。
1599年新教徒迫害のためグラーツを追われ、1600年プラハでティコ･ブラーエの助手となった。
1601年　ブラーエが死亡。彼の膨大な観測データと、ルドルフ二世の宮廷天文学者の地位も受け継ぐ。
惑星の運動に関するコペルニクスの説を信じていた。６個の惑星をピタグラスの５つの正多面体にはめ込む研究(これをケプラー　第０法則ということがある)。ティコ･ブラーエの惑星に関する２０年にわたる観測結果を入手し、火星の軌道を計算した。しかし、８分の誤差が生じた。最初からやり直し６年かかって1609年第1法則、第2法則を見いだした。続いて1619年第3法則を発見した。
1615年　母が魔女裁判。（1621年に無罪）
1630年11月15日　バイエルンのレーゲンスブルクへ向かう途中で死去。

         
      　　　　　　　　　      　　　　　　　　　      　　　　　　　　　      　　　　　　　　　      　　　　　　　　　      　　　　　　　　　      　　　　　　　　

戻る

---

 ティコ・ブラーエ(Tycho Brahe 1546〜1601)
デンマークの天文学者。初め法律を学び、のち天文学に転向。
1560　日食を観測して、数学と天文学に興味を持つ。コペンハーゲン、ライプニヒ、などの大学で学ぶ。
1572年11月、カシオペア座に超新星が現われる。485日間にわたり観測、新星の視差を測定しようとしたが、小さすぎて確認できないことに気がつく。これは、月より遠くに位置し、天上界に起きた現象であり、天上界は完全不滅であるという考えが崩れる。
1576 デンマーク王フレデリク２世の援助でウラニエンボルク天文台を建て２０年間惑星の位置観測に没頭、1572年の新星の観測とすい星の観測から、アリストテレスの宇宙像を疑問視するようになり、月と太陽が地球のまわりを回り、惑星は太陽のまわりを回るという独自の宇宙像を唱えた。
1597 プラハに移住し、ドイツ皇帝ルドルフ二世に仕える。
1598 プラハ天文台長、1600年にケプラーがその助手となった。ブラーエの観測は望遠鏡発明以前のものとしては最も精度が高く、ケプラーが３法則を導く資料となった。

戻る

---

アイザック･ニュートン(Isaac Newton 1642 - 1727)
　ニュートンはガリレオが亡くなった年に生まれた。父は、ニュートンが生まれる３か月前に亡くなっている。３歳の時、母親は農場主と再婚し。ニュートンは祖母に預けられた。１１歳の時、母親の２度目の夫も亡くなり、ニュートンはまた母親のもとに帰った。ニュートンは生涯独身であった。
　1665年イギリスにペストが流行し、大学は閉鎖された。ニュートンは、郷里の母親のもとに帰った。この期間に、二項定理を発見し、万有引力の考えが浮かんだ。1666年りんごの木の下で、ニュートンが休んでいると、りんごの実が落ちてきて、その瞬間に万有引力を着想したと、される。
   『同じ年に私は月の軌道にまで及ぶ重力について考え始めた。そして、一つの球面に内接して回る球体がその球面を押す力を求める方法を見いだし、それと、惑星の周期は軌道の中心からの距離の3/2乗に比例するというケプラーの法則を用いて、惑星をその軌道上に保つ力は回転の中心からの距離の２乗に反比例するはずであるということを導いた。またそれより、月をその軌道に保つのに必要な力と、地表面上の重力を比較してみると、きわめてよい近似で満足な結果が得られた。これらはみなペストが流行した1665年と1666年の2年間のことである。というのも、そのころの私は創造期の絶頂を迎えており、以後のどんなときにもまさって数学や哲学の問題に関心を注いだからである。』
とあるが、数学的不備と地球の半径等の知識不足から完成を得なかった。15年後に再度考察し、それまでの研究を著作「プリンキピア＝自然哲学の数学的原理」にまとめた。しかし、王立協会が出版を拒否、友人のハレーの援助で出版することができた。
また、1666年　光の分散の研究、1668年　反射望遠鏡の製作などの業績がある。
  微積分法の発見をめぐって、ライプニッツ（数学者、ドイツ）との論争、フック(バネ弾性などのフックの法則で知られる)との引力の逆２乗法則をめぐる論争がありニュートンはフックが王立協会の書記を努めるかぎり協会に論文を出すつもりはないと断言。フックが1703年に亡くなると、ニュートンは協会の会長になった。
  最終的には神経障害者となり、「神の存在を証明する方程式」の発見などに没頭した。それでも、下院議員や造幣局長官、王立協会会長等を勤めた。 これだけの業績があるにも関わらず、「･･･私自身にとって、私は浜辺で遊ぶ少年のように思われる。私は、時々なめらかな小石やふつうより美しい貝殻を見つけては喜んでいる。しかし、真理の大洋は、すべて未発見のまま私の前に横たわっている』の言葉はよく知られている。

  戻る