問題解答 戻る
問68
(1) 鉛直下向きを正にすると
mg-k x
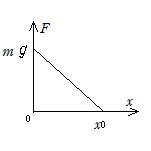
(2) 求める値をx0とすると,mg-k x0=0 より
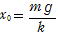
(3) 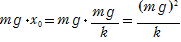
(4) 手が小球に与える力の大きさFはmg-k xで右図のように変化する から,グラフの面積が求める値である。
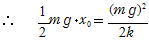
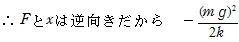
(5) 自然長の位置を高さの基準にし,力学的エネルギー保存の法則より
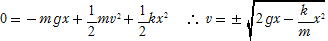
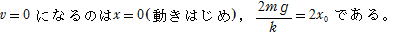
(6) 支えを急に取り去った場合,ゆっくり下降させた場合の2倍の伸びになる。これはゆっくり下降させる場合,手が小球に(4)の仕事をするためであり,
自然長の位置と(2)の状態の力学的エネルギーの差が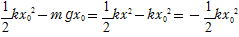 であることからわかる。支えを急に取り去った場合は
であることからわかる。支えを急に取り去った場合は
力学的エネルギー保存は保存されている。
問69
(1)求める加速度をα とすると 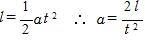
(2)求める速さをvとすると 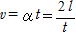
(3) mg l
(4)力学的エネルギーの変化量⊿Eは
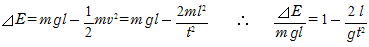 倍
倍
問70
(1)求める値をx とすると,小物体についての力のつり合いから

(2) 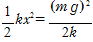
(3)力学的エネルギー保存の法則から
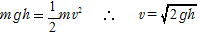
(4)縮んだ長さをl とすると,力学的エネルギー保存の法則から
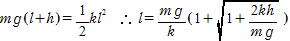
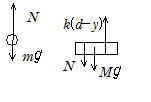
問71
(1)ばね定数をk とすると,つり合い式は
(m+M)g=k d
小球の加速度をα,小球が板を押し力をN とすると運動方程式は
小球 mα =N-mg
板 Mα =k(d-y)-Mg-N
両式から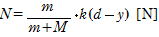
(2) (1)からN=0になるのはy=d で小球は板から離れる。(つまり自然長)
(3)求める速さをvとすると,力学的エネルギー保存の法則から
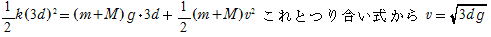
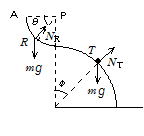
問72
(1)A点,R点について力学的エネルギー保存の法則から,R点での速さをvRとして
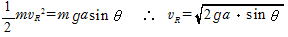
PR方向の力のつり合いから,抗力をNRとして
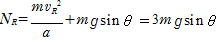
(2) T点での力のつり合いから
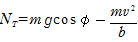
(3) NR=3mgsinθ ≧0だからAS間で面を離れることはない。Sを通過直後に面を離れるのでφ =0でNT=0として 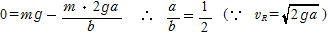
問73
(1)AC間の高さの差はlcosθ だから,C点でのおもりの速さをvとすると,力学的エネルギー保存の法則から
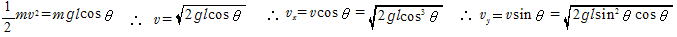
(2) C点のx座標,y座標をそれぞれxC ,yCとすると,xC=lsinθ,yC=-lcosθ
C点からD点に達するまでの時間をtとすると,vy-gt=0より
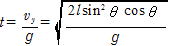
D点のx 座標,y座標をそれぞれxD,yDとすると,
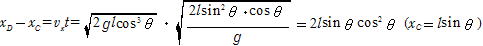
xD=lsinθ +2lsinθ cos2θ ∴ xD=lsinθ (1+2cos2θ )
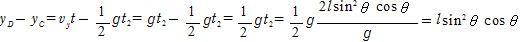
∴ yD=-lcosθ +lsin2θ cosθ =-lcosθ (1-sin2θ )=-lcos3θ
(3) xD=lsinθ (1+2cos2θ )=lsinθ {1+2(1-sin2θ )}=lsinθ (3-2sin2θ )
sinθ =u とすると z=sinθ (3-2sin2θ )=3u-2u3
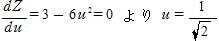 のときzは極値をとる。
のときzは極値をとる。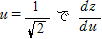 は正から負になるからこのとき極大である。
は正から負になるからこのとき極大である。
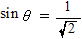 より
より 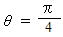
問74
(1) ma=N-mgcosθ
(2) 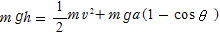
(3) (1)(2)より 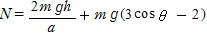
(4) (2)で v=0として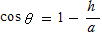 (この条件を満たすにはh<a)
(この条件を満たすにはh<a)
(5) (3)でN=0,θ =π として 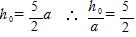
[参考] 半径 l のなめらかな円弧面内の最下点に初速度v0で質点を動かした場合鉛直下方となす角度がθ のところで,質点が円弧面から受ける抗力をTとすると,質点の運動範囲は以下の通り。 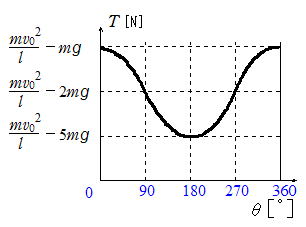
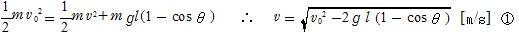
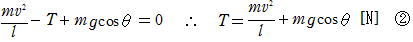
①,②から 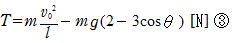
(1) 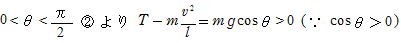
よって,面から離れない。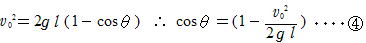
v=0になる位置は①から
0<cosθ <1 だから 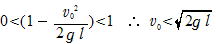
(2) 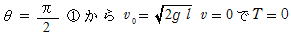
(3) 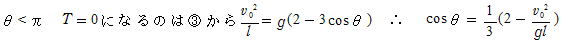
(4) θ ≧π でT>0 なら円運動を続ける。T=0 でもv>0だからT≧0 として③より 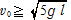
この条件を満たせば円運動し続けることができる。
なお,軽い棒を回転させた場合運動範囲の条件はvだけで決まるから(T=0でもかまわない),(3)は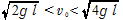 に変わる。
に変わる。
戻る