�@�@�@ �@�@
������ �x�N�g���a�͉E�}��H�ł���C���̋�����
�@�@�@�@�@
���� �߂�
��115
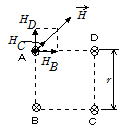
�����a�C�b�C�c�𗬂��d�����C�����`�̈ʒu�ɍ�鎥�EHB�CHC�CHD�͉E�}�̒ʂ�B���ꂼ��̋�����
�@�@�@ �@�@![]()
������ �x�N�g���a�͉E�}��H�ł���C���̋�����
�@�@�@�@�@![]()
��116
(1) �����`�𗬂��d���̑傫����IA[A]�Ƃ����
�@�@�@�@![]()
(2) �����a�𗬂��d����D�_�ɍ�鎥��̌����͎��ʕ\�����łȂ���Ȃ�Ȃ�����C�d���̌����͉������BD�_�̎����0�ɂ���悤�ȓ���B�̓d����IB[A]�Ƃ����
�@�@�@![]()
(3) �R�C�������S�n�ɂ��鎥��͎��ʗ����\�̌����łȂ���Ȃ�Ȃ�����C�d���̌����͔����v�܂��B���SO�̎����0�ɂ���R�C���̓d����IC[A]�Ƃ����
�@�@�@�@![]()
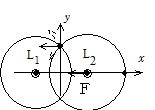
��117
(1) �݂��ɑł������̂� 0
(2) ![]()
��118
(1) x��a�Cx���|a�ɂ���d��I ������x ����̎������xB1�CB2�͂��ꂼ��
�@�@�@�@![]()
�ł���B
���@Bx��0�CBz��B1�{B2��![]()
z����̎������xB1'�CB2'�͂��ꂼ�� B1'��B2'��![]()
![]()
Bz��B1'sin�Ɓ|B2'sin�Ɓ�0
(2)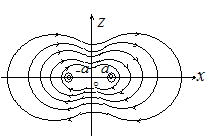
(3) (1)��� x��0�Cz��h��Bz��0�C![]() �������͂̌����́{z�����ł��̑傫��F�� F��BxJ l��
�������͂̌����́{z�����ł��̑傫��F�� F��BxJ l��![]()
(4) (3)�̗�F�Əd��mg���荇������ 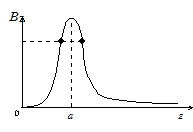
![]()
��������![]()
h�̉��ɕ���������̂́Cz�����Bx��z�ɂ��Ĕ������čő�l�����߂��Bx��z��a�ōő�Cz��0�C���� 0 �ɂȂ�B�܂�z��a�ɑ��đΏۂȈʒuz��Bx�̓�����������邽�߂ł���B
(5) �荇�����߂�h�����݂��邽�߂ɂ�(4)��h���������������Ƃ������ł���B�����
(��0IJ l)2�|(2��mga)2��0
���@��0IJ l��2��mga �� ![]()
��119
(1) f��qvB��1.6�~10-19�~2.0�~105�~0.40��1.28�~10-14��1.3�~10-14[N]
(2) ���E�ɓ������Ƃ��C�z�q�͐i�s�����E���Ƀ��[�����c�͂���B����(�E�˂�)�̖@�������b�̌���
(3) ���[�����c�͂����S�͂ƂȂ�~�^��������C�O�����a��r�Ƃ���Ɖ^����������
![]()
(4) (3)����O�����ar�͎��EB�ɔ���Ⴗ��B���EB���Q�{�ɂ����r��1/2�{�ɂȂ�B
(5) ����T�́C�z�q�̎��ʂ�m�Ƃ����![]() �ŗ^�����C�����ƊW���Ȃ��̂ŁC�P�{
�ŗ^�����C�����ƊW���Ȃ��̂ŁC�P�{
��120
(1) f��qvBsin��[N]
(2) OP�Ԃ̏��v���Ԃ͎���T������
![]()
(3) ![]()
(4) ![]()
(5) (2)����CT��B�ɔ���Ⴗ�邩��![]() �ɂȂ�B
�ɂȂ�B
��121
[1] x���̕��C[2] y���̕��C[3] ���C[4] ���C[5] y���̕��C[6] x���̕�
[7] ���[�����c�͂Ɠd�ꂩ��̗͂̂荇������
�@�@�@�@�@�@evB��eE2 �� v��E2�^B
[8] ![]()
[9] ��RR��![]() �C�d��V=E1l ���
�C�d��V=E1l ��� ![]()
[10] ![]()
��122
(1) I [A]�̒����d�����狗��r [m]�̓_�ɂ����鎥�E�̋���H [A/m]��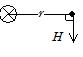 �@
�@![]() �ŕ\�����B���̌����͉E������d���̗��������ɐi�܂���ƂɉE�˂�����]��������B
�ŕ\�����B���̌����͉E������d���̗��������ɐi�܂���ƂɉE�˂�����]��������B
(2)(�)�E���̓d���ɂ�鎥�EH1�ƍ����̓d���ɂ�鎥�EH2�̌����͐}�̂悤�ɂȂ��Ă���B
�@�@�@���E�̋����͂��ꂼ�� ![]() �ł���B
�ł���B
�@�@�@�������E��x�Cy������H���CH���Ƃ����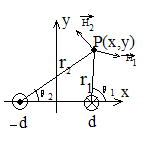
�@�@�@�@�@�@Hx��H1sin��1�|H2sin��2�CHy���|H1cos��1�{H2cos��2
r1�Cr2�C��1�C��2��
�@�@�@�@�@![]()
�@�@�@�@�@![]()
������C����炩��
![]()
(�)�C(�)�����̓d�����E���̓d���̂Ƃ���ɍ�鎥�E�̋�����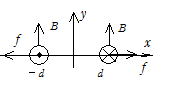
�@�@![]()
�ł���C�����́{y�����ł���B
�������x�́@B����0H ������C�����̓d���̒P�ʒ����ɓ�����f �� f��IB��![]()
�ł���C�����͉E�˂��̖@������{x�����ł���B�����̓d���ɂ��E���̓d�����瓯���傫���̔��Ό����̗͂���̂ŁC�Q�̓d���Ԃɂ͐˗͂������B
��123
(1) x ������![]() �Cy������
�Cy������![]()
(2) x������![]() �Cy������0
�Cy������0
(3) �����P�C�Q�Ԃ̗͂ƈړ���������ɒ������邽�߁B