(20-1)式から
またPQ内で電子は磁界からP→Qの向きに力を受けるから,Qが負に帯電することになりPの方が電位が高い。
(微小長さdrでの起電力 dV はdV=Bvdr である。全起電力は B,ω が一定で v=rω だから
問題解答 戻る
問124
PQが単位時間に描く面積は![]() だから,
だから,
(20-1)式から ![]()
またPQ内で電子は磁界からP→Qの向きに力を受けるから,Qが負に帯電することになりPの方が電位が高い。
(微小長さdrでの起電力 dV はdV=Bvdr である。全起電力は B,ω が一定で v=rω だから
![]() )
)
問125
(1) 磁束の最大値はφ=Ba2[Wb],横軸は速さが v だから図に示す目盛りになる。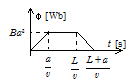
(2) 0≦x≦a:コイルを上向きに貫く磁束が増加するから,時計まわりに誘導電流が流れる。誘導電流は
![]()
a≦x≦L:磁束が変化しないから誘導電流は流れない。
L≦x≦L+a:コイルを貫く磁束が減少するので,誘導電流は反時計まわりに流れる。誘導電流の最大値は ![]()
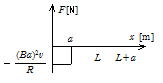
(3) 0≦x≦aのとき,電流が磁界から受ける力は左向きに BIa=![]() である。a≦x≦L では誘導電流が流れないから力は受けない。
である。a≦x≦L では誘導電流が流れないから力は受けない。
L≦x≦L+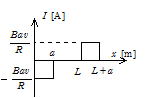 aでは誘導電流は流れているが辺abは磁界の外に出ているから力を受けない。
aでは誘導電流は流れているが辺abは磁界の外に出ているから力を受けない。
問126
(1) スイッチを入れた直後は導線は動いてないの誘導起電力は0である。
電流I は ![]()
(2) 求める力 F は F=I l B =![]()
(3) 誘導起電力V ' はvBlだから ![]()
(4) 導線の加速度をαとして運動方程式を立てる
mα=IBl ∴ α=![]()
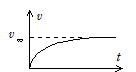
(5) v が十分大きくなると(3)から I=0 になる。
よって,E=v∞Bl ∴ ![]()
問127
(1) V=vBlcosθ (2) ![]()
(3) (2)の結果と F=ilB から ![]()
(4) 十分時間が経過すると,重力の斜面方向成分と電磁力がつり合って棒は等速度運動になるから
mgsinθ=Fcosθ=(![]() )cosθ ∴ v=
)cosθ ∴ v=![]()
問128
(1) φ=φ0cost=BScost [Wb]
(2) ![]()
(3) ![]() (4)
(4) ![]() (5)
(5) ![]()
問129
(1) ![]()
(2) ![]() ,PL=0
,PL=0
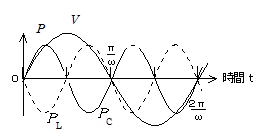
(3) 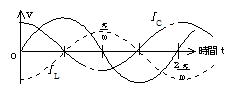 (4)
(4) 
問130
(1) ZL=2πf L より
![]()
(2) V=I・ZL=0.50×40=20[V]
(3) V=IZ=![]()
問131
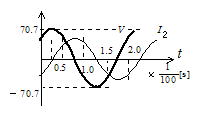
(1) グラフから,周期が2.0/100[s]だから,周波数は50[Hz]
(2) 自己インダクタンスをL,コイルにかかる電圧を V とすると,角振動数ω はω=100πだから V=I1・Lω
∴ ![]()
(3) 求める値を V とすると,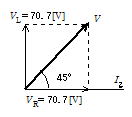
V=I2・Lω=![]()
(4) 電気抵抗にも電流 I2 が流れる。電気抵抗の最大電圧は
![]()
である。R,L での位相は右図のようになるので I2 と電源電圧の位相差は45゚ である。
(5) コイルの電圧は電流より90゚位相が進んでいるから下図のようになる。