m=ρ1V1=ρ2V2だから,ボイル・シャルルの法則から
問題解答 戻る
問85
一定質量mの気体を考える。2つの状態での密度,体積,温度,圧力をそれぞれρ1,V1,T1,P1,ρ2,V2,T2,P2 とすると,
m=ρ1V1=ρ2V2だから,ボイル・シャルルの法則から
![]()
問86
浮上するときの気球内の空気の密度をρ,温度をT とする。気球内の空気の圧力は大気圧P0と等しいから,問85の式から
ρ0T0=ρT
気球が静止しているときの力のつり合い式は
ρ0Vg=ρVg+Mg
両式からTを求めて ![]() ∴
∴ ![]() 以上
以上
問87
角度θ の場合のガラス管内の空気の圧力pθはpθ=p0-lsinθ,θ =0 の場合はp0だから,ボイルの法則から
p0x0=pθxθ=(p0-lsinθ )xθ ∴ ![]()
θ=90°の場合は上式から ![]()
問88
(1)(a)分子の球形容器へ衝突での速度変化は,壁に垂直に2vcosθ だから
⊿p=2mvcosθ
(b) A点から次の衝突点B点までの距離は ![]() =2acosθ だから
=2acosθ だから
衝突から次の衝突までの時間間隔は ![]()
(c) 単位時間当たりの衝突回数は ![]()
(d) 分子1個から器壁が受ける力は ![]()
(2)(a) N個の分子から受ける力は ![]()
(b) 器壁の全面積は4πa2だから,圧力pは ![]()
一方,球の体積Vは![]() だから
だから ![]()
(c) 全気体分子の運動エネルギーの総和Eは ![]()
一方,理想気体の状態方程式は pV=RT だから ![]()
問89
(1) D
(2) 半径D,高さvt の円柱の体積を求めればよいから πD 2vt
(3) 密度n=![]() である。(2)の円柱中のt秒間の分子数はπD2vt・nだから単位時間に衝突する回数は
である。(2)の円柱中のt秒間の分子数はπD2vt・nだから単位時間に衝突する回数は ![]()
(4) 分子は単位時間にv 進み,この間πD2vn回他の分子と衝突する。求める距離をr とすると
![]()
(5) ![]() 倍
倍
(6) 分子数は変わらないので密度はK倍
(7) 温度一定だから1倍
(8) (4)のr はn に反比例するから ![]() 倍
倍
問90
(1) B,C点の温度をそれぞれTB,TCとして状態方程式から
P0V0=RT0, (3P0)V0=RTB, P0(3V0)=RTC
∴ TB=TC=3T0 (イ)(ロ)
(2) 等積変化だから気体は仕事をしないので ⊿U=Qである。
![]()
(3) TB=TCだから⊿U=0 (しかし途中では変化あり) Q=W である。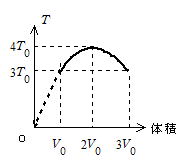
![]()
(4) 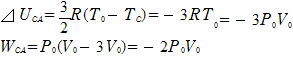
∴ QCA=⊿UCA+WCA=-5P0V0=-5RT0
∴ 放出熱量は5P0V0(=5RT0)
(5) BC間のPとV の関係を式で表すと
![]()
これと PV=RTより
![]()
問91
A→B:Q=0, ![]() ⊿U,W は負
⊿U,W は負
B→C :W=P2 (V1-V2) (ピストンが気体に仕事をするから正),
![]() Qは負
Qは負
⊿U=Q-W=![]() ⊿U は負
⊿U は負
C→A:W=0,Q=CV(TA-TC)=![]() ⊿U,Qは正
⊿U,Qは正
問92
冷蔵庫内の熱を放出するためのモーター回転による仕事の一部が熱に変わり,導線での発熱もある。このため扉を開けて十分時間が経過すると,他の方法より室温が上がる。