問16
問17
問18 投げ上げてから再び地面にもどる時間は最高点までの時間t1の2倍だから,初速度は v0=g t1=9.8×(4.0/2)=19.6[m/s]
問題解答 戻る
問15 ![]()
問16 ![]()
問17 ![]()
問18 投げ上げてから再び地面にもどる時間は最高点までの時間t1の2倍だから,初速度は v0=g t1=9.8×(4.0/2)=19.6[m/s]
よって, 14.7=19.6t-gt2 t2-4t+3=0 (t-1)(tー3)=0 ∴ t=1.0,3.0 [s]
問19 (1) 初速度の水平,鉛直成分はそれぞれv0sinθ,v0cosθ だから
x=v0cosθ・t ・・・・① y=v0sinθ t-g t2・・・・②
(2) 傾きが-xtanαの原点を通る直線の式 y=-xtanα・・・・③
(3) 衝突するまでの時間を t とすると①②③式から
v0sinθt-gt 2=ー v0cosθ・t・tanα
t > 0 だから
(4) lcosα=x=v0cosθ・t より
(5) v0,α 一定だから(4)のlが最大になるには sin(2θm+α)=1
∴ 2θm+α=90゚ ∴このとき
問20 (1) 投げた点を原点,鉛直上向きをy軸の正の向きとし,初速度をv0とする。
3.0[s]後に変位が同じになるから
1.8×3.0=v0×3.0-(1/2)×9.8×3.02 ∴ v0=16.5 [m/s]
(2) 3.0[s]後の小石の速さをv1とすると
v1=v0-g t=16.5-9.8×3.0=-12.9[m/s]
よって,気球に対する小石の相対速度
(小石の速度-気球の速度)は
-12.9-1.8=-14.7[m/s] ∴ 鉛直下向きに 14.7[m/s]
(3) 投げてからt ' [s]後に地面に達するものとすると
-40=16.5t ' -×9.8×t '2 ∴ t ' =5.0[s] (負号は不適)
∴ すれ違ってから2.0[s]後
問21 (1) Aを落下させてからすれ違うまでの時間t は ![]()
Bの初速度をv0とすると,鉛直投げ上げの変位の式から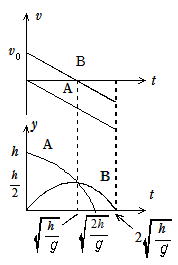
(2) Aを落下させてからA,Bが地面に達するまでの時間をt1,t2とすると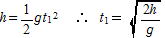
問22 花火のOを原点とし水平方向にr軸,他の座標を図のようにとる。ry平面内に分布した玉について考える。破裂してから t 秒後の座標r,yは
r=v0tcosα,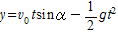
角度αは0≦α≦2πの範囲である。
上式からαを消去して(自乗して辺々加える) r2+(y+gt2)2=(v0t)2
また, r2=x2+z2 ∴ x2+(y+gt2 )2+z2=(v0t)2
これはの点を中心に半径v0tの球の式である。時間t に比例して半径が大きくなり,かつ球の中心は下方に一定加速度gで落下する。よって,打ち上げ花火は上空から見ても,地上から見ても球形が落下するように見える点では見る場所によらないことがわかる。