ホーム  メニュー            波動    波の性質    音波   ドップラー効果  弦振動気柱振動    光波の諸性質    幾何光学
                                                                             

１３−２ 波の性質
　波の性質として反射，屈折，回折，干渉がある。このうち，反射，屈折，回折は「ホイヘンスの原理」，干渉は「重ね合わせの原理」で説明できる。

　波の重ね合せの原理と干渉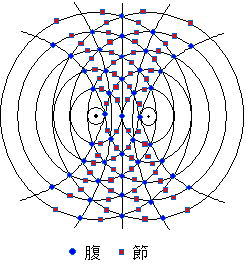

重ね合せの原理(principle of superposition)
   「２つ以上の進行波が媒質中を進むとき，任意の位置の合成波の変位は，個々の波による変位の代数和で与えられる」
という。右図は水波を上から見たものであり，Ａ，Ｂが波源で，同位相(振動状態が同じ。つまりAが山のときBも山)であるものとする。実線が山，点線が谷を示すものとする場合，実線どおし，点線どおしの交点は波が強め合っている場所，実線と点線の交点は弱め合っている場所である。
Ａ，Ｂからの波が互いに向かい合っている位置(ＡＢ間など)では，強め合う位置を「腹」,弱め合う位置を「節」という。互いに振幅，速さ,波長が等しい波が向かい合って干渉すると「腹，節」が現れる，定常波ができる。定常波で「節」は常に振動しない位置であり，「腹」は各瞬間ごとの最大変位を示す位置である。
波源Ａ，Ｂが同位相でそれぞれからの距離がl₁，l₂の位置で
　　　強め合う条件は　｜l₁−l₂｜＝ mλ 　         (13-3)
　　　弱め合う条件は  ｜l₁−l₂｜＝     (13-4)
 　　λ は波長，mは干渉次数(m＝0，1，2，3，･･･)
重ね合わせの例  

    (右上図にマウスを置くと動画になります)

　右図で波Aと波Bの変位の和を描いたものが波Cである。それぞれの位置で確かめてみよ。

  (右図にマウスを乗せると解答が表示される)

定常波(standing wave)
 　腹，節を持ち，進まない波。定常波は，同位相で波長，振幅，速さが等しい２つの波が互いに干渉してで
　きる。一定の振動数を発する気柱振動弦振動などがその例である。また，右上図で波Aと波Bが互いに向か
　い合って干渉すれば，図中の波Cの変位が0の位置が定常波の節になっている。

「ある時刻の波面から出される素元波の包絡面が新しい波面になる」
というもので，波が伝播すること，反射，屈折，回折の現象を説明することができる。

                        (図にマウスを置くと動画になります)

                                      
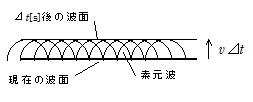
                             平面波の伝わり方の説明                                  球面波の伝わり方の説明

右図の波源Pからの波が右向きに円形波として進行し，波面Sができた場合を考える。次の時間間隔で半径SS₁とする素元波が波面Sから連続して作られると，波の前方包絡面S₁が作られるともに後方の包絡面S₂が作られることになるが，現実にはS₂の波面(逆行波)はできない。これがホイヘンスの原理の不完全な点である。これは，波が時間的に不規則に生じた刺激が次々に伝わっていく現象と考えていたためであり，同時にホイヘンスの原理では回折現象を説明できない。
このホイヘンスの原理の欠点を解決したのがフレネルである。フレネルによると
  「重ね合わせの原理を，ホイヘンスの原理と組み合わせ，各点から出た素元波を重ね合わせたとき，その合成振幅に相当する強さがそこで観測される効果である」
とみなした。これをホイヘンス−フレネルの原理という(1836年)。つまり，各点から作られる 素元波を，問題になる点で重ね合わせたとき，その合成振幅に相当する強さがそこで観測される波の効果であると見なした。フレネルによると素元波の振幅は波の進行方向からの角度を右図のようにθ，振幅をφ(θ )とすると，θ ＝π およびθ ＞でφ＝0，θ＝0で極大値になるとした(右図フレネルの仮定参照)。これに対してキルヒホッフは数学的にこれらを考え，φ(θ ) ∝ (1＋cosθ)とした(上図キルヒホッフの仮定参照。振幅の大きさと線の太さが比例)。つまり，後方の包絡面S₂が作られても，振幅が0なので逆行波は生じないというものである。
 (一般に言われるホイヘンスの原理はホイヘンス−フレネルの原理のことである)

図のように壁に向かってきた平面波は，板で反射される。波面ＡＢがＡ'Ｂ'に反射する場合波面ＡＢから素元波が作られ，それらの包絡面が新波面Ａ'Ｂ'になる。
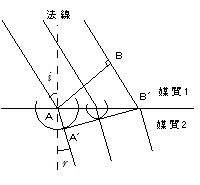
このとき，境界面上の反射点Oの法線(反射板に直交する方向に引かれた線)と入射波の斜線 (入射線)との作る角i を入射角，反射波の射線(反射線)と法線との間の角i'を反射角という。反射点での入射線と反射線は，その点の法線と同一面にあり，下図で △ACC₂≡△C₂A₂Aから，入射角と反射角は常に等しい。
反射の法則 入射角 i＝反射角i '

                                                               
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(図にマウスを置くと動画になります)

        屈折(refraction)

波がある媒質の中から異なる媒質の中へ進むとき，波の速さが変わるために，波の進行方向が変わる現象を屈折という。
  下図で境界面の上下で波の速さが異なるので，ＡＡ'＜ＢＢ'となるため屈折が起こる。２つの媒質１，２の境界面に立てた法線と入射線との間の角(入射角)をi，法線と屈折線の射線(屈折線)との間の角(屈折角)をr，媒質１，２での波の速さをv₁，v₂，波長をそれぞれλ₁，λ₂とすると，媒質１に対する媒質２の屈折率n₁₂は次式で与えられる。
　　　      (13-5)
「入射角，屈折，屈折角の正弦の比は入射角に関係しないで一定である」を屈折の法則という。

                                                                     
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(図にマウスを置くと動画になります)

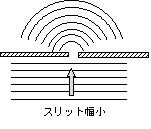
        回折(diffraction)

平面波がスリットの下から上に向かう場合，波の波長がスリット幅より長いと，直線だった波面がスリットを通過するときに，素元波からの包絡面が円形になり，スリットを通過した後は波面が円形波に変わる。これはスリットの裏側に回り込むことを示している。このように，障害物の背後に波がまわりこむ現象を回折という。
　回折は，波の波長が隙間の間隔より長くなると顕著に現れる。物かげで音を発したときに音は聞こえるが姿が見えないのは，音の波長(可聴音の波長は1.7cm〜17m程度)が光の波長(可視光の波長は4〜7×10^-7m程度)より長いために起こる現象である。
                                                               
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(図にマウスを置くと動画になります)

重ね合わせの原理は1755年弦の定常振動を研究していたベルヌーイ(1653-1716)が弦の各点の変位が倍振動の変位の和となることを，力学的に示した。これが重ね合わせの原理であり，数学的にはフーリエが完成させた。

反射の法則は，ユークリッドの｢光学｣ 「反射の光学」に”平面・曲面におけるの法則”が記されている。またヘロンも，入射角＝反射角について，またルクレティウスも反射の法則を記している。

屈折の法則は1615(1620の説もある)にスネルによって発見されたので，スネルの法則ともいう。1644年 デカルトが論文｢光学｣で確認している。

回折は1665年グリマルディによって発見された現象。後に，1815フレネルが投獄された牢屋の中に差し込む光で回折理論を考えた。

    波の強さ

波の進行方向に垂直な単位面積を単位時間に通過するエネルギーで表され，これを波の強さという。
単振動のエネルギーEは，で与えられる。[10-2 力学エネルギー保存−単振動のエネルギー参照]
ρを媒質の密度，f を振動数，A を振幅とすると，単位体積中の波のエネルギーE/Vは， だから，v を波の速さとすると，
波の強さI は    である。        
または，
(波のエネルギーの時間的割合つまり仕事率P は，波の進行方向に垂直な断面積をSとすると )[J/s]
  単位断面積当たりの仕事率が波の強さだから，

このことから，波の強さI は I ∝(f A)²，つまり振動数，振幅それぞれの自乗に比例する。
波の強さの単位はJ/s･m²＝W(ワット)/m²である。
           
           振幅と音源からの距離の関係
         球面波                             　　　　　　     　　　　　平面波
              波源からr での強さをI(J/m²･s)とすると                               球面波の場合と同様にして                          
P(J/s)＝4π r²×I                            P(J/s)＝2π r×I (高さを1mとする)
                 

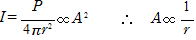
波が反射現象を示すときに，固定端での反射のみ位相が逆になる(位相が逆とは，変位の正負が逆になる，つまり入射波の山が谷になる)。
自由端反射で位相変化は起こらない。固定端は，音波が固体，液体に反射する場合や弦が固定されている端点で反射する場合，光の場合屈折率の小さな物質から屈折率の大きな物質への反射(例えば空気から水への反射)などである。
　 右図はウエーブマシンでの位相変化を図示したものである。波は右から左へ正の変位のパルス波が伝わっている。自由端の場合は正の変位のまま右方に反射して進み，固定端の場合，負の変位に変わって右方に反射して進んでいる様子がわかる。固定端の場合，進行波と反射波の変位の和が必ず0になるため，位相が逆になると考えることができる。

    ばねのかたさに違いによる位相変化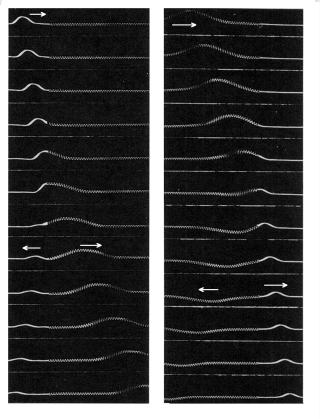

かたさの違う(ばねネ定数の違う)ばねを接合し，パルス波を送った場合にも位相変化が起こる場合がある。
かたいばねから柔らかいばねへの境界を通過するパルスでは，パルスは境界を一部透過し一部が反射する。入射パルスは反転されない。(右図左)
                                     
柔らかいばねからかたいばねへの境界を通過するパルスでは，パルスは境界を一部透過し一部が反射する。入射パルスは反転される。(右図右)
                                  　　　

     反射による位相変化の作図法
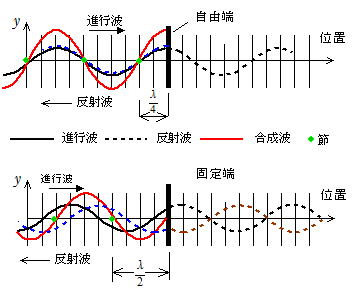自由端反射
  �@ 進行波を自由端から先まで進んだものとして作図する(左図自由端から右の点線)。
  �A �@の点線を自由端で線対称に左右折り返す(自由端から左側の青色点線)。これが反射波である。
  �B 進行波と反射波を重ね合わせの原理によって変位の和を作図して合成波を作図(赤色実線)する。
    自由端に最も近い節は自由端からの位置であり，節の間隔はである。
 固定端反射
  �@ 進行波を固定端から先まで進んだものとして作図する(左図固定端から右の点線)。
  �A �@の黒色点線を上下反転し(茶色線)，これを固定端に線対称に左右折り返す(固定端から左側の青色点線)。これが反射波である。
  �B 進行波と反射波を重ね合わせの原理によって変位の和を作図して合成波を作図する(赤色実線)。
固定端の最も近い節は固定端からの位置，節の間隔はである。

自由端反射による定常波の定式化
x＝Lに自由端があるものとする。
進行波の変位y₁が   の場合
x＝Lでの(自由端での)進行波の変位は 
x＝Lでの(自由端での)反射波の変位y₂は，位相変化がないから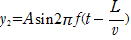  
任意の位置xでの反射波の変位はy₂(x，t)，x＝Lからの時間の遅れが だから，
       
これは，反射波の見かけ上の波源が，自由端に対して対称位置x＝2Lにあり，ここからだけ時間が遅れていることを示している。
合成波の変位yは
       
        (t の入っているsinの項が時間変動項，入ってないcosの項が時間に関係しない振幅項である。)
節の位置は時間に関係なく振幅が0，つまり振幅項が0だから
       
        (x＝0で節なら これが閉管の振動数 ⇒ [弦振動気柱振動参照])
固定端の場合

反射波の変位が自由端の場合と変わり，x＝Lで
       
任意の位置x では
       
合成波の変位は
       
x＝0で節なら
             ∴  

ホーム  メニュー            波動    波の性質    音波   ドップラー効果  弦振動気柱振動    光波の諸性質    幾何光学
           Top