ホーム メニュー ![]() 波動 波の性質 音波 ドップラー効果 弦振動気柱振動 光波の諸性質 幾何光学
波動 波の性質 音波 ドップラー効果 弦振動気柱振動 光波の諸性質 幾何光学
15-5 鏡とレンズ
鏡
平面鏡による像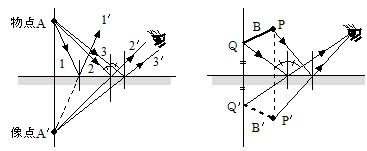
物体が点状の場合,物点Aから出された光線が平面鏡で作る像点A ' を考える。
光線1,2,3ともに平面鏡で反射の法則によってきまる方向に反射される。左図の光線2,3の反射光が目に入り,見かけの光源(これが像点A ' )から光が出ているように感じる。
物体PQが棒状の場合,P,Qからの光線は平面鏡に入射し,反射の法則によってきまる方向に反射する。
この結果,右図のように平面鏡に対して線対称の像P' Q' が作られるので目にはPQの倒立像が見える。
 球面鏡による像
球面鏡による像
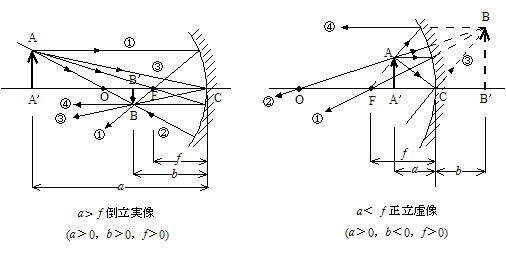
(1) 凹面鏡(開きが小さい場合)
作図のための光線
① 光軸に平行光を凹面鏡に当てると焦点に集まる
② 球面の中心Oを通る光線は,反射後同じ経路をもどる
③ 鏡の中心に向かう光線は,光軸に関して対称に反射する
④ 焦点に向かう光は,光軸に平行に進む
結像の式
左図より
α+φ=γ,γ+φ=β
∴ α+β=2γ ・・・・・①
また
h≒atanα≒aα α=h/a
h≒btanβ≒bβ β=h/b ・・・・・ ②
h≒Rtanγ γ=h/R
②式を①式に代入して
a→ ∞ のとき b=
∴倍率=
 |
 |
 |
 |
 |
| 上の凹面鏡 | 下の凹面鏡 | 横から見た図 | 斜めから(子豚半分) | 上から見る(浮上) |
(2) 凸面鏡
光が収束しないので実像は結ばず,その前面にある物体の像はいつも物体より小さく正立の虚像が鏡の裏側にできる。
結像の式
左図より
γ+φ=β,α+γ=φ ∴ β-α=2γ ・・・・・ ①
また
h≒atanα≒aα α=h/a
h≒btanβ≒bβ β=h/b ・・・・・ ②
h≒Rtanγ≒Rγ γ=h/R
②式に①式を代入して
a→∞のとき b==f (焦点距離)
∴倍率=
レンズ(=「平たい豆」の意味のラテン語)
(1)凸レンズによる像
結像のための光線
① 光軸に平行な光は焦点に進む
② レンズの中心Oを通る光はそのまま直進する
③ 物体側の焦点F1を通ってレンズに入る光は光軸に平行に進む
(a) 図解から結像式を導く
△OAA '∽△OBB 'より
△OPF2∽△BB' F2 より
OP=AA ' だから(15-11)
倍率mは m=または,
から
∴ m=
(aはレンズ前方を正(実物体)とする。a<0は虚物体。bはレンズ後方を正とする(実像),b<0は虚像。
焦点距離の求め方
左図でレンズAによってが成り立つが,同時にa,bを入れ替えても成り立つ。
a+b=L,b-b'=b-a=d
両式から
∴
実験的にはこの値と,太陽光を使って測定した値を比較してみることができる。
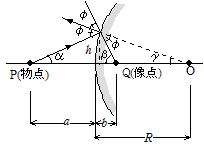
(b) 屈折の法則から結像式を導く
凸面の場合
屈折の法則から
n1sini=nsinr
∴ r≒0 として n1i=nr ・・・ ①
△OAPで φ+α=i
△QAOで β+γ=φ
∴ γ=φ-β ・・・ ②
φ+α=i≒・・・ ③
α,β≒0 として(近軸近似)
AB=h とすると図より
h=PBtanα≒atanα≒aα α=h/a
h=QBtanβ≒btanβ≒bβ β=h/b ・・・ ④
h=OBtanφ≒R1tanφ≒R1φ φ=h/R1
③,④から
∴・・・ ⑤
( a →で b → ∞)
a<では
凹面の場合
屈折の法則から
n2sinr '=nsini ' r ' ≒0 として n2r ' =ni ' ・・・ ① '
△OAP ' で i '+α'=φ'
△QAOで β'+φ'=r ' ・・・ ② '
① ',② 'から
n2(β'+φ')=n(φ'-α') ∴ n2β'+nα'=φ' (n-n2) ・・・ ③ '
図より AB=h として
h=BP 'tanα' ≒a 'tanα' ≒a 'α' α'=h/a '
h=Q ' Btanβ'≒b 'tanβ' ≒b 'β' β' =h/b ' ・・・ ④ '
h=OBtanφ' ≒R2tanφ' ≒R2φ' φ' =h/R2
③ ',④ 'から
∴・・・ ⑤ '
右凸面で⑤式から(曲率半径R1)
・・・ ⑥
左凹面で⑤ ' から(曲率半径R2) → a '=-(c-t)
・・・ ⑦
⑥+⑦から (t ≒0 として)
n1=n2=1 とすると
a → ∞ となるとき b=f として(これが焦点距離)
∴
虫めがね
左図において,凸レンズの結像公式で b=-(d-l)
倍率mは m=
l=f (目を焦点上に)→ m=,l=0 → m=1+
(2) 凹レンズによる像
凹レンズの作図に使う3つの光
① 光軸に平行な光は手前の焦点F1から出たように進む
② 光源と反対側の焦点F2に向かう光は光軸に平行に進む
③ レンズの中心Oに進む光はそのまま進む
△AA' O∽△BB' Oから
△OPF1∽△BB' F1から
∴
∴(15-12)
まとめ
レンズの式(15-13)
a:物体とレンズまでの距離(a>0)
b:レンズと像までの距離(実像でb>0,虚像でb<0)
f:焦点距離(凸レンズは f>0,凹レンズは f <0)
倍率mは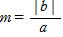
15-1 反射・屈折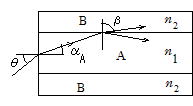
問99 図のように屈折率n1の媒質Aが屈折率n2の媒質Bにはさまれた層状の光学素子がある。ただし,外側の空気の屈折率を1とし,n1>n2>1であるとする。
(1) 図のように外側から入射角θ で光が媒質Aに入射したとき,屈折角α と入射角θとの間の関係を求めよ。
(2) 媒質Aに入射した光は媒質Bとの境界面で一部が反射し一部が媒質Bに入る。光が媒質Bに入るときの屈折角β と角α の間の関係を求めよ。
(3) 光が媒質Aに入射するときの角度θがある条件を満足すると,媒質Aに入った光は媒質Bとの境界面で全反射して媒質Bには入らない。
その必要十分条件を求めよ。
15-2 回折・干渉
問100 図1のように,2個の細いスリットA,Bをもつ薄くて不透明なついたてFの左方に単色光を発する光源Sがあり,ついたてFの右方にスクリーンWが置かれている。スリットの幅a は単色光の波長λ に比べて十分小さく,スリットの間隔2d は波長の数倍以上の大きさである。光源SからついたてFまでの距離と,ついたてFからスクリーンWまでの距離は等しくL で,L は2d に比べて十分大きい。
(1) スリットを通った光は,スクリーン上に,図2に示すような強度分布の干渉縞を生じた。もっとも明るい線P0ととなりの明るい線P1との間隔をr として,λ とr の関係式を求めよ。必要なら,1に比べて十分小さい数εに対して成り立つ近似式を利用せよ。
(2) 光源Sをy軸の正の方向へd だけ移動させると,スクリーン上のもっとも明るい線P0はどちらの方向へどれだけ移動するか。
問101 空気中から波長λの平行な光が厚さd の薄膜に入射する。その場合の光の干渉について考える。薄膜の屈折率はnであり,空気の屈折率は真空の屈折率と等しいとせよ。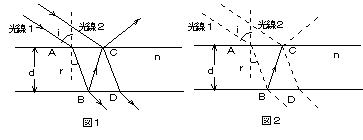
(a) 図1のように角度iで薄膜に光が入射するとき,入射角i と屈折角r との関係を答えよ。
(b) 点Aで薄膜に入射した光線1は,薄膜の裏側の点Bで一部反射し,点Cにおいて光線2と干渉する。
光線1と光線2の行路差を表す線分を図2の中に補助線などを含めて記入し,その行路差Lを屈折角rを用いて答えよ。
(c) 前問(b)で求めた行路差Lに対する光線1と光線2の位相差を答えよ。なお,点Bでの光線1の反射波は,位相を変化させないことに注意せよ。
(d) 点Dから出てくる光が強め合う条件を求めよ。
問102 図のように平面ガラス板の上に曲率半径R の平凸レンズを置き,その上方から波長λの単色光を当てる。このとき反射光を上から観察すると同心円の明暗の縞模様が見える。次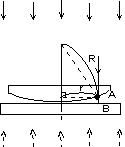 の問いに答えよ。
の問いに答えよ。
(1) レンズの下面の点A,ガラスの上面の点Bの反射で光の位相はそれぞれどうなるかを説明せよ。そのことと関連づけて,縞模様の現れる理由を説明せよ。
(2) m番目の明るい縞の半径r をRとλを用いた式で表せ。ただし,ガラスとレンズの間にはさまれた空気の層の厚さは,Rに比べて十分小さいものとする。
(3) ガラスとレンズの間を屈折率n の液体で満たしたところ,同心円の縞模様の半径が変化した。その理由を説明せよ。このとき,中心からm番目の明るい縞の半径r 'は,間が空気の場合のm番目の半径r の何倍になるか。nはガラスの屈折率より小さいものとし,空気の屈折率は1とする。
(4) ガラスの下方から波長λ の単色光を当てて透過光を上から観察した場合も,同心円の縞模様が見える。反射光の場合の縞模様との違いとそのようになる理由を説明せよ。
15-5 レンズ
問103 薄い凸レンズLがある。Lの前方15[cm]のところに長さ3[cm]の物体Aを光軸に垂直に置くと,Lの後方30[cm]のところに光軸に垂直においたスクリーンSの上に明瞭な像ができた。
(1) Lの焦点距離はいくらか。
(2) AとSは動かさないでLをAから遠ざけると,再びS上に明瞭な像ができた。
(a) Lははじめの位置から何[cm]移動しているか。
(b) 像の長さはいくらか。
(3) AとLとを動かして,長さ7.5[cm]の像をS上に結ばせたい。
(a) AとLの距離
(b) LとSの距離をそれぞれいくらにすればよいか。
ホーム メニュー 波動 波の性質 音波 ドップラー効果 弦振動気柱振動 光波の諸性質 幾何光学
Top