または,Aからの重心位置を求めると
同様に,AB方向の重心位置はABの中点からBへ
問題解答 戻る
問31 AD方向について
GからAに向かった重心位置をxGとすると
または,Aからの重心位置を求めると
同様に,AB方向の重心位置はABの中点からBへである。重心位置はFからBへ
問32 
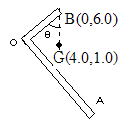
(1) AOが水平になるように支える点Hが重心位置だから,Oからの重心位置xGは
12×6.0=18・xG ∴ xG=4.0cm
(2) y方向の重心位置yGは
6.0×3.0=18・yG ∴ yG=1.0cm
∴ (xG,yG)=(4.0,1.0cm)
(3) Bでつると,鉛直線下方に重心Gがあるので
問33 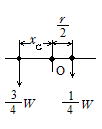
(1) Oからの重心位置をxGとし,半径rの円の重さをW とすると
∴ OB線上OからBへ
(2) Oからの重心位置をxGとすると,比重がもとの3倍の円板の重さは
∴ xG=
∴ OB線上Oから
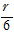
問34 Oからの重心位置をxGとすると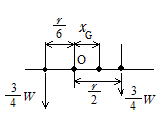
π(R2-r2)x G=πr2d ∴
Bからの重心位置は
問35 x軸方向の重心位置xGは
y軸方向の重心位置yGは yG=8cm
問36
(1) 糸a,bの張力をそれぞれTa,Tbとすると
水平方向の力のつり合い式は,右向きを正として
-Tasin30+Tbsin45=0・・・・①
鉛直方向の力のつり合い式は,上向きを正にして
Tacos30+Tbcos45-1・g=0・・・・②
①②式から
(2) A端から重心Gまでの距離をxGとすると,B点まわりの力のモーメントのつり合いから
(1-xG)cos30×1×g-1×Ta=(1-xG)cos30×1×g-1×(-1)g=0
∴
問37 「傾いた」とは f =0である。B点まわりの力のモーメントのつり合い式は
F×(L-l )+f×l-W×(l-L/2)=0
∴
f=0 として
[別解] 鉛直方向の力のつり合い式 f+N-F-W=0
A点まわりの力のモーメントのつり合い式 F×L+W×(L/2)-N×l=0
の両式からNを消去しても同じ結果が得られる。
問38 棒に働く力は,ひもの張力T,重さW,壁からの抗力Fである。示力図を描くとFの向きが決まる。
座標軸を図のように決める。Fのx,y軸方向の成分をそれぞれFx,Fyとする。A点まわりの力のモーメントのつり合い式は
W・(l/2)-Tsinθ・l=0 ∴
x軸方向の力のつり合い式は
Fx-Tcosθ=0 ∴
y軸方向の力のつり合い式は
Tsinθ-W+Fy=0 ∴ Fy=W-Tsinθ=
F と Fxのなす角度をφ とすると
問39 座標軸を図のようにとる。Fのx,y軸方向の成分をそれぞれN,Rとする。
A点まわりの力のモーメントのつり合い式
T・( l/2)-W・l cosθ=0 ∴ T=2Wcosθ
x軸方向の力のつり合い式は
Tsinθ-N=0 ∴ N=2Wsinθ・cosθ
y軸方向の力のつり合い式は
Tcosθ-W-R=0 ∴ R=Tcosθ-W=W(2cos2θ-1)
N と F のなす角度をφ とすると
問40 OからTの作用線までの距離はr cosθ である。OG=aとし,半球と水平面との接点をCとすると,∠COG=θだから,
OからWの作用線までの距離はasinθ である。Cでの垂直抗力をN とすると,鉛直方向の力のつり合いから,
T+N-W=0 ・・・①
O点まわりの力のモーメントのつり合いから
T・r cosθ-Wasinθ=0 ・・・②
θ=45゚でT=だから
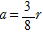
②式から
これと①式から