�z�[�� ���j���[ ![]() ���_������� �x�N�g���ƃX�J���[ ���̂̉^�� �� �^���̖@�� �~�^�� �d���ƃG�l���M�[ �^����
���_������� �x�N�g���ƃX�J���[ ���̂̉^�� �� �^���̖@�� �~�^�� �d���ƃG�l���M�[ �^����
�y�U�z�́@
���̂ɗ͂������Ɖ^���̏�Ԃ��ω�����B�͊w�̖ړI�́C���̂ɓ����͂Ɖ^���Ƃ̊W�𖾂炩�ɂ��邱�Ƃł���B���̂ɓ����͂ނ���ƁC���̂̐ڐG�ɂ���ڐG��(�R�́C���C�́C���̂�����(����)�́C�˂Ȃǂɂ��e����)�C�d�́C�d���͂Ȃǂ̏�̗�(���u��)������B
6-1 ���낢��ȗ�
(1) �d��(gravity)�d���̂�n���������́B���m�ɂ́A���L���͂ƒn�����]�ɂ�鉓�S�͂� �x���g���a�ł���B
�x���g���a�ł���B
(2) ����(tension)�d�d�ڐG�������Ă��镨�̊Ԃň��������́B
(3) �e����(elastic force)
�˂̒e���� f (�˂����R���ɖ߂낤�Ƃ����)�Ƃ˂̐L�k�� x ��(����͈͂̔͂ł�)���W�ɂ���(�t�b�N�̖@��)�B
�t�b�N�̖@���� f ���|kx �ŕ\�� ��C���萔k���˒萔(�e���萔)�Ƃ����B
(4) ���C��(frictional force)�C�����R��(normal force)
�����őe���ʏ�ɒu���ꂽ���̂ɐ��������ɗ͂�������ꍇ�C�͂�����傫���ȉ��ł͕��̂������Ȃ��B����͖ʂ��畨�̂ɕ��̂̉^����W��������ɖ��C�͂������Ă��邩��ł���B������C�Î~���C���Ƃ����B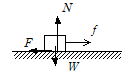
���̂ɉ�����͂�傫�����A����l���傫���Ȃ�ƕ��͓̂����o���B���̂������o�����O�̖��C�͂��ő喀�C�͂Ƃ����B���̂������Ă���Ƃ��ɓ����Ă��門�C�͂�(�^)�����C�͂Ƃ����B
�ʂɐ����ȕ������畨�̂���͂𐂒��R�͂Ƃ����B�����R�� N �ƍő喀�C��F0�̊Ԃɂ�
F0����0N (����) (6-1)
�̊W(��0��Î~���C�W���Ƃ���)�C(�^)�����C��F ' �Ɛ����R�� N �Ƃ̊Ԃɂ�
F '����N (����(�^)�����C�W���Ƃ���)�̊W������B
��ʂ���0�����ł���B�����ɒu���ꂽ���̂ɁC�����ɉ������� f �Ɩ��C�� F �̊W�͉E�}�̂悤�ł���B
���C�̌�����
�@ ���ʐ� (���̐ڐG�ʂɂ��鉚�ʂǂ��������ݍ����ɂ���R�͂������ł���Ƃ����)
�A �Ò��� (���ʐ��ɂ��ƕ��̕\�ʂ��قlj��ʂɂ�門�C����������͂������C�t�ɂ��ꂢ�ɖ������قǒ�R�͂��������邱�Ƃ��m���߂��Ă���B�����ꂽ�\�ʂɂ��������̂ǂ����̕��q�Ԃ̗�(������Ò��͂Ƃ���)�����C�̌����ł���Ƃ����)
(5) ����(buoyancy)
�A���L���f�X�̌����ɂ���
�u����(�C�́C�t��)���̕��̂́C���ꂪ�r�����Ă��闬�̂̏d���ɓ��������͂�����������Ɏ�v
�r���������̖̂��x�����C�̐ς�V�C�d�͉����x��g �Ƃ���ƁC���͂���Vg �ŗ^������B
6-2 ���_(particle)�ɓ����͂̂荇��
�@ ���_���Î~���Ă������(�E��)�́C���_�ɓ����̘͂a��0�ł���B���W����x�Cy�ɂƂ�x�������̗̘͂a��Fx, y�������̗̘͂a��Fy �Ƃ���ꍇ�C�荇���̏�����Fx��0�CFy��0
�A �͂��荇���Ƃ��C���͐}(����)������B
�d��W�̎��_�ɐ����ɗ� F �������C�荇���ۂ��ĐÎ~����ꍇ�C���_�����Ă鎅�̒��͂�T�C�E�}�̊p�x���� �Ƃ���ƁCF�CW�CT�����ɕ`���Ď��͐}��`���Ɨ̓x�N�g��������B
���W���E�}�̂悤��x�Cy�Ƃ���ƁC
�@�@x�������̗͂̂荇������ F�|Tsin����0
�@�@y�������̗͂̂荇������ Tcos���|W��0
�܂��́C���͐}����C

�ł��邱�Ƃ��킩��B
�͂͑��ݍ�p������C�͂ɂ͌����̕��̂�����B�����牽�ɓ����͂��𖾂炩�ɂ��邱�Ƃ��̐S
f �� x �͈̔͂�e��(elasticity)�͈͂Ƃ����Bk �̒P�ʂ�N/m�B���͈̔͂��z����ƑY��(plasticity)�͈͂Ƃ���
F0����0W�łȂ����Ƃɒ���
���C�̖@����1699�N�ɃA�����g�����������C1781�N�ɃN�[�������m�F�����@���ŁC�A�����g���|�N�[�����̖@���Ƃ������B
���C�ɂ��āC���̂��ڐG�ʂ𐂒��ɉ����͂����ɑ傫�������ɏ������ꍇ�������Ăقڐ�����������I�@���B�ő�Î~���C�͂Ɠ����C�ɂ��ẮC�ڐG�ʂ̖ʐςɂ͖��W�ł���B�^�����C�ɂ��Ă͂���Ɂq���C�͉͂^�����x�ɂ͖��W�ł���r�B
�Î~�̏�����,���m�ɂ́A���́�0 ���C�����x��0�̏ꍇ�ł���B�����x��0 �̏ꍇ�C���́�0 ���Ɠ����x�^��������
���͐}�́A�̓x�N�g�������ɘA�����ĕ`�����}
�����R�͂̍�p�_�͕��̂̒��S�Ƃ͌���Ȃ����Ƃɒ���
�����R�͂͂ǂ��ɓ����̂�
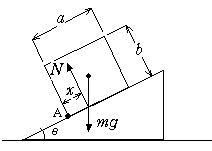
�@�@�����Ɗp�Ƃ��Ȃ����C�̂���Ζʏ�ɁA�ӂ̒�����a�Ab �ŏd��mg �̒����̂�u���B���̂��]�|���Ȃ��͈͂ōl����B�����R�͂�N �AN ��A�_����̋�����x �Ƃ���ƁAmg �� N �̍�p���͈�v���邩��
�@�@�@
�@�@���̌��ʁA�]�|���Ȃ� tan�Ɓ��ia/b�j �͈̔͂ŁA�����R��N �̍�p�_�͊p�x�Ƃɂ���ĕω����邱�Ƃ������Ă���B�����ʏ�ł̓Ɓ�0 ������ x ��(a/2)�A�܂蕨�̂̒��S�ł���B
�͂̂荇�����l����|�C���g
�͕͂��̂��^��(�Î~)���錴���ł���B�͂𐳊m�ɔ����o�����߂̎菇�͎��̒ʂ�B
�@ �Ώە���(�����A�Ƃ���)���o���B
�A �Ώە��̂ɓ����d�͂������o���B
�B �Ώە��̂ɐڂ��Ă��镨�̖�(B,C�Ƃ���)�������o���B���ꂪA�ɓ����͂̌������̂�����B����A,C����A�ɓ����ڐG�͂������o���B
�C �A�C�B�̗͂́C���ׂ悤�Ƃ�������ւ̐��������������A���̌��������߁C���̍��͂����߂�B
��1 �E�}�̂悤�ɂ�������y���˂Ɏ����C�˂̏�[�Ɍy���������C�������Ŏx���S�̂��Î~���Ă���B�肪���������͂����߂�B
�� ���ꂼ��̕��̂�Ɨ����Đ}�������̂ɓ����͂������o���B���ꂼ��̕��̂ɓ����͈͂ȉ��̂Ƃ���B
�@ ������F�d (�˂�������������́��˂̒e����),�e (�d��W���n�����炨����ɓ�����)
�A �ˁF�b (�����˂������́����̒���)�C�c (�����肩��˂ɓ�����)
�B ���F�` (�肩�玅�ɓ�����F)�C�a (�˂��玅�ɓ�����)�B
�@�@���̌��ʁC�` �� �a�C�b �� �c�C�d ���e ���荇���Ă���̂ŁCF��W�ł���B
��2 �E�}�̂悤�ɁC�����őe����(�Î~���C�W����)��ɏd��W �̕��̂�u���C�����ƂȂ��p�x���ɊO�� f �������Î~���Ă���
�@�@�荇�����������B
�� ���̂ɓ����͂�
�@�@���������F�O��f �̐�������fcos���C�Î~���C��F
�@�@�@�@�荇���� fcos���|F��0
�@�@���������F�䂩��̐����R��N�Cf �̉�������f sin���C�d��W
�@�@�@�@�荇���� N�{fsin���|W��0
F0����0W�łȂ����R
N��W�|f sin�� F0����W�ł͂Ȃ��B����0 �̏ꍇ�̂� N��W
�Î~���C�W����0�̑���@
�@ ��2�ɂ���������0�Ƃ��Cf ��������葝��������B���ׂ�o�����O�� f��F0������0�̏ꍇN��W �����炩����0������ł���B
�A �E�}�̂悤�ɐ����Ɗp�x�����Ȃ��Ζʏ�ɕ��̂�u���B�������X�ɑ傫����������0���z����ƕ��̂͂��ׂ�o���B���̂Ƃ��Î~���C��F�͍ő喀�C��F0�ɂȂ�Bx�Cy�������̗͂̂荇���́C
�@�@�@x�������Fmgsin����F0����0N�Cy�������FN��mgcos��
�������� (��0�C�p�Ƃ���) ��0�� tan��0 (6-2)
�܂�C�Ζʂ̌X�������X�ɑ傫�����C���̂����ׂ�o�����Ƃ��̊p�x��0�𑪒肷�����0���^������B
�^�����C�W�����̑���@
�@ ��0�̑���Ɉ��������� �������C���̂��Ζʂ����ׂ�~���Ƃ��C�^�����C��F ' ��mgsin�� ���荇���ē����ŗ���������悤�Ȋp�x��' �����߂���B������'�����������߂���B
�A �����ʏ�ɕ��̂�u���C������^���Ă��ׂ炷�ƁC���C�͂��Č������Î~����B���̂Ƃ��C����������xa�̑傫������g�ɂȂ�̂Ł@�@�@�@����a�^g �ŗ^������B
���K���
��23 �}�̖��Ŏ������͂́C�����牽�ɓ����͂��B
��24 �`�N���a�N���C�a �N�����������Ă���B�}�̖��Ŏ������͉͂����牽�ɓ����͂��B
��25 �V�䂩�畨�̂����ł艺�����B�}�̂悤��,���̂ɂ�F�CW�̂Q�͂������Ă���B
F�CW�͂��ꂼ�ꉽ���牽�ɓ����͂��B
��26 �y�����P�C�Q�ɂ���ċ��P�C�� �Q���艺�����Î~���Ă���B���P�C�Q�ɓ����͂������o���B
��27 �����ȏ��̏�ɕ���A,B���d�˂Ēu���Ă���B����B�ɓ����Ă���͂�}���ɖ��Ŏ����C���̗͉͂����牽�ɓ����͂�����B
��28 �{�[���𓊂���ƁC��������`���Ĕ��ł����B��C��R�╂�͂��Ȃ����̂Ƃ���ꍇ�C�{�[���ɓ����͉͂����B
��29 �Î~���Ă���{�[�g�ɏ���Ă���l���ݕǂ���������C�{�[�g�͓����o�����B�{�[�g�Ɛl���ꏏ�ɓ����o�������͉͂����B
��30�S���h��G���y�����Ԃɂ��������[�v�̈�[�ɂƂ���C�̏d�vH�̏�ɏ�����l�����̃��[�v�̑��[����������C�S���h���������畂������ԂőS�̂��Î~�����B
�@ �l�ɓ����͉͂���
�A �S���h��G�ɓ����͉͂����B
[��]
��23 �u���[�v���甠�v�ɓ����́B�l�����������̂łȂ��C���[�v�����������Ă���
��24 �uB�N���甠�v�ɓ����́BA�N��B�N�������Ă��邪�C���ډ����Ă���̂�B�N�����B
��25 �uF�͎����畨�́v�C�uW�͒n�����畨�́v�ɓ����́B
��26 �u��1�ɂ͎�1�C��2�C�n���v�C�u��2�ɂ͎�2�C�n���v����͂������B
��27 �u�d��(�n������)�������C�����������CA���牺�����v(���͐}�̏�Ƀ}�E�X���悹�Č���)
��28 �u�d�́v
��29 �u�ݕǂ��l�������́v
��30 �l�u�d�́CH�C���[�v����v�CG�u�d�́CH�C���[�v����v
6-3 �傫���̂��镨�̂̂荇��
�@�@��������ό`���Ȃ��L�����������
(1) �d�S
�@�@�@�@���̂̊e�����ɓ����d�͂̍��͂̍�p�_���d�S�Ƃ����B�d�S�ŕ��̂��x����ƁC���̂̓o�����X���Ƃ��]���Ȃ��B
�@�@�@�@����m1�Cm2�C��� �̏����̂����W(x1�Cy1)�C(x2�Cy2),��� �ɂ���Ƃ��C
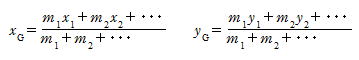 (6-3)
(6-3)
�@�@�@�@���d�S�ʒu�ł���B
(2) ���̂ɓ�����
�͂̕\����
�傫���C��p�_�C��p��
�@�@�͂̃��[�����g
�@�@�@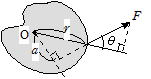 �͂ɂ́C���̂s�ړ���������C�ό`�����铭��������ƂƂ��ɁC��]���܂��ɕ��̂���]�����铭��������B��]������͂̓��������̂܂��
�͂ɂ́C���̂s�ړ���������C�ό`�����铭��������ƂƂ��ɁC��]���܂��ɕ��̂���]�����铭��������B��]������͂̓��������̂܂��
���͂̃��[�����g�Ƃ����B
���}�ʼn�]���n�܂��̗͂̃��[�����g�̑傫���́C�n����͂̍�p���ɉ��낵�������̒��� a (�����r�̒�����
����)�ƁC�͂̑傫��F �Ƃ̐ςŕ\�����B
�͂̃��[�����g�̑傫��M ��
�@M��Fa��Frsin��
(�� �͉�]���n����͂̍�p�_�Ɉ���������(����r )�Ɨ͂̂Ȃ��p�x)
���̂���]���Ȃ������́C���鎲�܂��̗͂̃��[�����g���荇���Ă��邱�Ƃł���B
(3) ���̂ɓ����͂̍���
�@ �͂̍�p�������ʂ̏ꍇ
�@�e�͂̍�p�_�����ʂɂ��āC�͂̑㐔�a�����́B
�@�@�@�@�@����F��F1�{F2
�A �͂̍�p���������ꍇ
�@�@�e�͂̍�p���̌�_�Ɋe�͂̍�p�_���ڂ��C���s�l�ӌ`�̌����ō��͂����߂�B
�@�@�@ ����
�B �͂����s�œ��������̏ꍇ
�@�@���͂̑傫���͊e��F1�CF2�̘a(F1�{F2)�ŗ^�����C�����͂Q�͂Ɠ��������B
���͂̍�p���͂Q�͂̍�p�_�Ԃ̋������C�Q�͂̑傫���̋t��ɓ�������_��ʂ钼���ł���B
�@�@�@�@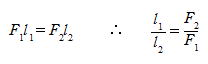
�@�@(F1�Ɂ|f�CF2��f�������C�����̍��͂̍�p���̌�_�����͂̍�p���ƌ����)
�C �͂����s�ŋt�����̏ꍇ
�@�@���͂̑傫���͊e��F1�CF2�̍�|(F1�|F2)|�ŗ^�����C�傫�����Ɠ��������ł���B��p�_�͂Q�͂̍�p�_�Ԃ�
�@�@�������C�Q�͂̋t��ɊO������_�ł���B
(F1�Ɂ|f�CF2��f �������C�����̍��͂̍�p���̌�_�����͂̍�p���ƌ����)
�D ����
�@�@�P�g�݂̌��ɔ��Ό����̕��s�͂����͂Ƃ����B
�@�@���͂̍��͂͂O�ł���B�E�}�ŗ͋��͂̂n�_�܂��̗͂̃��[�����gM��
�@�@�@�@�@�@M��F1(r2�|r1)��F1d �ŗ^������B
(4) ���̂̂荇��
�荇������
�@�E�}�̂悤��x�Cy���W���Ƃ�C�e�͂̕��͂�Fx�CFy�Ƃ���B
�@�@�@�@x�������̗͂̂荇�� ��Fx��0 (F1x�{F2x�{�����0) (6-4)
�@�@�@�@y�������̗͂̂荇�� ��Fy��0 (F1y�{F2y�{�����0) (6-5)
�@ �n�_�܂��̗͂̃��[�����g�̂荇��
�@�@�@�@�@�@ ��M��0 (M1�{M2�{�����0) (6-6)
���̂̂荇�����l����|�C���g
�@�@�@�@ �͂̃��[�����g�̂肠����
�@�@�@�@�@�͂̑傫���~(�͂̍�p���Ɨ͂̎n�_�܂ł̋���)��,�E�܂��(�܂��͍��܂��)�𐳂ɂ���B
�@�@�@�@�@�C�ӂ̓_�܂��̗͂̃��[�����g�̘a��0 ����]���Ȃ������ł���B
�@�@�@�A ���̂̂荇����
�@ �@�@�@�͂̂荇��������сC�C�ӂ̓_�܂��̗͂̃��[�����g�̂荇������K�v�Ȗ��m���������𗧂Ă�B
�R �傫���̂��镨�̂̂荇��
��31 �}�̂悤�ɂP�ӂ̒�����a�̔�����l�Ȑ����`�̔�ABCD����C�ʐς����̂S���̂P�̐����`��������c��̕���
�@�@�@ABCDEFG�̏d�S�̈ʒu�����߂�B
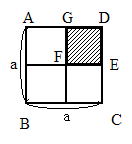
��32 ����18cm�̐j��AB��A�[����12cm�̓_O�Œ��p�ɐ܂�Ȃ��āC�k���^�ɂ����j��������B�j���̑����Ɩ��x�͈�l�ł���C
�@�@�@����܂Ȃ��Ƃ���B
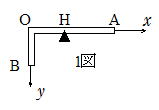
(1) �P�}�̂悤�ɁCAO�������ɂȂ�悤�Ɏx����_H�́CO���牽cm�̂Ƃ��납�B
(2) O�����_�COA������x���COB������y�����߂�Ƃ��C�k���^�j���̏d�S�̍��W�����߂�B
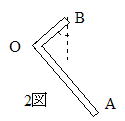
(3) �Q�}�̂悤�ɁC�k���^�j����B�[�Ɏ������Ă邵���Ƃ��COB���������������ƂȂ��p�x���� �Ƃ���Ƃ��Ctan�� �̒l�͂�����ɂȂ��Ă荇�����B
��33 ���ar�̈�l�Ȍ����̉~��O������B���̂P�̔��aOA�a�Ƃ��鏬�~��O'������ʂ����B
�@�@�@(1) �c��̔̏d�S�̈ʒu�����߂�B
�@�@ (2) ����ʂ����~�`�̌��ɁC���~�Ƒ傫���������������ŁC��d�����Ƃ̂R�{�ł���悤�ȉ~���͂ߍ��ނƂ��C�S��
�@�@�@�@�@�̏d�S�̈ʒu�͂ǂ��ɂȂ邩�B
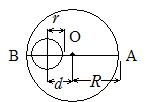
��34 ���a r �̉~�����a R �̉~�̒��SO���狗�� d ����Ă���ʂ���Ă���B�d�S�ʒu�����߂�B
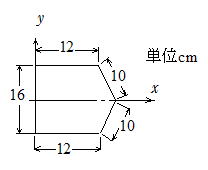
��35 �}�̐}�`�̏d�S�ʒu�����߂�B
��36 ���ʂP[Kg]�C�����P[m]�̖_AB��V�䂩��Q�{�̌y����a�Cb�ł邵���Ƃ���C�}�̂悤�ɂ荇�����B�d�͉����x�̑傫����g [m/s2]�Ƃ���B
(1) ��a�Cb�̒��͂͂��ꂼ�ꉽ[N]���B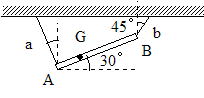
(2) �_AB�̏d�S�f��A�[���炢����̂Ƃ��납�B
��37 ����L�C�d��W�̈�l�Ȗ_���E�}�̂悤�Ɏx�_�`�C�a�Ŏx�����B�_�̉E�[�ɗ�F����������_���X�����B�`,�a�ł̐����R�͂�f�CN�Ƃ���F�����߂�B(99�����ǎ�)

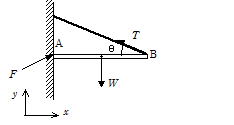
��38 �����̕ǂɏd��W�C����l�̋ώ��Ȗ_�𐅕��ɂȂ�悤�ɁC�����Ɗp�x�� ���Ȃ��ĂЂ������t���Đ}�̂悤�ɐÎ~�������B�Ђ��̒���T�C�_���ǂ�
���R��F�����߂�B
��39 �y���Ē��� l �̖_��}�̂悤�ɐ����Ɗp�x�����Ȃ��āC�Ђ���_�ƒ��p�ɂȂ�悤�ɓV�䂩����t���C�d��W�̏�����_�̉E�[�Ɏ��t���ĐÎ~
������B�ǂł̍R�� F �C�Ђ��̒��� T �����߂�B(�_���̓q���g)

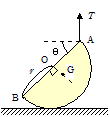
��40 �Ȃ߂炩�Ȗʏ�ɁC���ar�C�d��W�̔�����u���C���̈�[�`�Ɏ������āC�^��Ɉ����グ��B�}�̂悤�ɁC�f�ʂ������ʂƂȂ��p�x���� �Ƃ���
����45߂̂Ƃ��C����������������T�̑傫���͂ł������B�����̏d�SG�́C�f�ʂ̒��SO��ʂ�f�ʂɐ����Ȓ�����ɂ���B�}�̂悤�Ɋp�x����
�C�ӂ̒l�ł���Ƃ��C����������������T�C���������ɂ���ڂ������R�͂̑傫�������߂�B
�z�[�� ���j���[ ���_������� �x�N�g���ƃX�J���[ ���̂̉^�� �� �^���̖@�� �~�^�� �d���ƃG�l���M�[ �^����
Top