ホーム  メニュー            序論･物理量   ベクトルとスカラー  落体の運動    力    運動の法則  円運動  仕事とエネルギー  運動量
                                                                             

【１１】運動量(momentum)と衝突(collision)

複数の質点系での衝突，分裂などについて，新しい量として運動量を導入し，外力がはたらかない系(これを孤立系という)で運動量保存が法則されることを示す。

１１−１ 運動量と力積(impulse)

速度vで運動している質量mの質点の運動量p を(その質量)×(速度)と定義する。
         
運動量はスカラーmとベクトルvとの積だからベクトル量である。
運動量の次元はLMT^-1であり，単位はSI単位系ではKg･m/sである。
運動量と力積

質量mの質点がなめらかな水平面上を速度vで運動しているとき，点Aから速度の向きに一定の力Fを微少時間��tだけ加えたところ，点Bでの速度がv' になった場合，AB間の加速度はだから，質点についての運動方程式 から
よって，     (11−1)
と書くことができる。ここでF��tを力積という。
　力Fによる力積は質点の運動量変化に等しい
力積の単位はN･sだか，上式から運動量と同じ単位Kg･m/sでもあるが，通常はN･sを使う。
一般に力は右図のように時間とともに変化するから，力の時間平均Fを使うと力積I は，左図の斜線 部分の面積で与えられる。  
      I＝F��t   (11−2)
この関係は力積−運動量定理として知られ，ニュートンの第２法則と等価である。

質点の運動量が時刻t_Sで運動量P_Sから時刻t_Eでの運動量p_Eまで変化するとき，力と運動量の関係は  
つまり，質点に働く力が0の場合に運動量変化がないことがわかる。積分を使うと
力積I は   力の時間平均は   と定義される。

例1 静止している質量m＝50gのゴルフボ ールをクラブで水平と45ﾟの角度で上方に打ったところ，初速 度v₀が45m/sであった。ボールがクラブから受けた力積の大き さはいくらか。またボールがクラブに接触したまま運動する距離 はボールの半径r＝2.0cmとする。衝突時間��t はいくらか。

解   I＝��p＝mv₀＝50×10⁻³×45＝2.3[N･s]
         

例2 質量0.20Kgのボールが速さ20m/sで飛んでくる。このボールをバットで打ち返し，
(1) ボールを逆向きに30 m/sで打ち返す場合
(2)ボールの進行方向と90ﾟの方向に30 m/sで打ち返す場合，バットがボールに与えた力積はいくらか。

解  
(1) はじめの運動量の向きを正とすると(11−1)式から
             I＝0.20×(−30)−0.20×20＝−1.0×10¹[N･s]
     飛んでくる向きと逆向きに1.0×10¹ [N･s]の大きさ
(2) 右図より
             図の向きに7.2 N･s

例3 高さ5mの位置から質量1.0Kgのボールを自由落下させた。地面に落下して止まるとき，地面がボールに与える力積はいくらか。また，地面に触れてから止まるまでの時間を0.05[s]とするとボールが地面から受けた平均の力Fはいくらか。g＝10 [m/s²] とする。

解 5m自由落下したとき地面での速さは
         I＝mv＝1.0×10＝10N･s
         I＝��t からは

質問 ボールを素手で受け取る場合，手を引いて受け取ると痛さが軽減されること，コップをある高さから落下させた場合，床がコンクリートの場合の方が床に絨毯を敷いてある場合より割れやすいことを説明せよ。
     

[答] 捕球する前のボールの運動量mvは投手によって決められ，落下するコップの運動量は高さで決まる一定の値である。mv＝F tなので，t を大きくするとFが小さくなるため。 

１１−２ ２質点系の運動量保存

(1) 一直線上での衝突
 　右図のように質量m₁の質点Aが速度v₁，質量m₂の質点Bが速度v₂で同じ直線上を動いて衝突し，衝突後の速度がそれぞれv₁'，v₂'になったとする。衝突時の接触時間を��t，BがAから受けた力積をFtとするとAはBから力積−Ftを受ける。A，Bに対して(11−1)を適応すると
Aについて m₁v₁'−m₁v₁＝−Ft
Bについて m₂v₂'−m₂v₂＝ Ft
両式から
      （11−3）
が得られる。左辺は衝突前の運動量の和，右辺は衝突後の運動量の和を示している。
２質点が衝突で，両者間に働く力だけが働く場合，それらの全運動量は一定に保たれる。
(2) ２次元での衝突
（11−3）式の関係は下図のように２質点が２次元で衝突する場合も成り立つ。運動量の和は平行四辺形のベクトル合成の方法から衝突前後で             の関係が求められる。
                              
一般に，
        ２つの質点が衝突する場合，互いの内力だけ作用する場合，系内の運動量は一定に保たれる。
       これを運動量保存の法則という。

 A，B間でおよぼし合う力をF，F ' とすると，F ＝−F ' の関係にある。それぞれの運動量をp₁，p₂とすると
        ∴           ∴ p1+p2＝一定

分裂

静止している質量がそれぞれm，Mの質点A，Bが分裂しA，Bがそれぞれ，で動き出した。分裂前の全運動量は0だから，運動量保存の法則から
　　　0＝m＋M となる。
一般に，質量Mの物体が速度Vで運動中に分裂して質量m₁，m₂，･･･ m_nのn個に分かれそれぞれの速度が₁，₂，･･･ で運動する場合
    　M＝m₁₁＋m₂₂＋･･･m_nn が成り立つ。

１１−３ はねかえり係数と衝突

床，壁，斜面への質点の衝突では，運動量保存の法則を適応するには困難さがある。そこで図のように２質点の衝突前のそれぞれの速度をv₁，v₂，衝突後のそれぞれの速度をv₁'，v₂'として
           
衝突前後の相対速度の割合 （11−4）
をはねかえり係数として表す。
衝突は，はねかえり係数の値によって３つに分類できる。
いずれの場合も，運動量は保存される。
  e＝１ 弾性衝突(または完全弾性衝突)･･･  この衝突は，力学的エネルギーは保存される。
　0＜e＜1 ･･･　非弾性衝突。力学的エネルギーは減少する。                                      
　e＝0 ･･･  完全非弾性衝突 　力学的エネルギーの減少量が最も大きい。 (例6の[注]参照)

なお，なめらかな床，壁，斜面への衝突では，面と平行方向は面から力積を受けないので速さは変わらず，面と垂直方向の衝突後の速度＝e×衝突前の速度になる。なめらかでない場合は，面から受ける力積を考慮して計算する。
実験を見る
( にマウスを乗せると画像が表示される)空気潤滑装置(摩擦抵抗を限りなく小さくした台)上での実験(例6参照)
e≒1  M＝m    
e≒1  M＞m      
e＝0  M＞m      

例1 高さhから自由落下させたところ，床ではね返ってh' の高さまで達した。eを求めよ。ただし，鉛直下向きを正とする。
 
解 床に衝突する直前，直後の速さv，v' は自由落下と鉛直投げ上げの式から
         
よって，はねかえり係数の式（11−4）でv₂＝0，v₂'＝0 として
       
例2 質量m₁の質点が速さvで直線上を運動し，静止していた質量m₂の質点と一体となった。一体となった後の速さv' はいくらか。

解 運動量保存の法則から
        m₁v＝(m₁＋m₂）v'     ∴    
      m₁＝N･m₂の場合 ， (N＝1，2，3で  )
             
例3 質量m₁の質点が速さv₁で直線上を運動し，それと直角方向から速さv₂で進んできた質量m₂の質点が一体となった。一体となった後の速さと向きを求めよ。

解 求める速さをv とすると，運動量保存の法則から
         
    → この例で運動量がベクトルであることを再確認せよ

例4 質量M，長さlの板がなめらかな水平面上に置かれている。板の右端から質量mの人が板に対して速さuで左向きに等速で移動した。人が板の左端に達するまでに，板はどれほど動くか。

解 地面に対する人，板の速度をそれぞれv，Vとする。uは人の板に対する相対速度だから，左向きを正とすると
v−V＝u である。運動量保存の法則から
        mv＋MV＝0     ∴   mv＋M(v−u )＝0     ∴    
人が板の右端から左端までに移動する時間をt とすると   
求める値は，   人が動いた距離は
この結果から，人，板の移動した距離は質量に反比例することがわかる。

例5 質量がそれぞれm_A＝0.2Kg，m_B＝0.3Kgの小球A，Bがある。Aが速さ1.0m/sで進んできて，静止しているBに直線上で衝突した。衝突後のBの速さはAが進んできた向きに0.7m/sで動いた。衝突後のAの速度およびAとBのはねかえり係数を求めよ。

解 Aが進んできた向きを正とし，求める値をvとして運動量保存の法則を立てると
          0.2×1.0＝0.2v＋0.3×0.7  
Aが進んできたのと逆向きに0.05m/s
このとき，はねかえり係数e は       ← eのとりうる範囲は0≦e≦1であることを確認

例6 例5を一般化する。質量がそれぞれm₁，m₂の小球A，Bをなめらかな水平台に置き，Aを速度vで静止しているBに衝突させる。A，B間のはねかえり係数をeとする。衝突は直線上で行われる。衝突後のA，Bの速度v₁，v₂を求めよ。
 運動量保存の法則，はねかえり係数の式から
     m₁v＝m₁v₁＋m₂v₂      e v＝v₂−v₁
  両式から
       
　　ここで m₁＝m₂ かつe＝1の場合， v₁＝0，v₂ ＝v  つまり，速さが入れ替わる。
            0＜e ＜1 の場合 ，m₁＞em₂ でv₁＞0，v₂はつねに正
         e＝0 の場合 ，
[注]
ここで、この衝突による力学的エネルギーの変化量��E を計算すると
　　
この結果から e＝0 の場合 ��Eが最大、つまりエネルギーの減少が最大、e＝1 の場合��E＝0 つまり力学的エネルギーは保存されることが分かる。

                                            演習問題                                        解答

11-2 ２質点系の運動量保存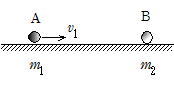
問75 それぞれの質量がm₁，m₂の小球A，Bがある。はじめ，Bは静止しておりAは速度v₁でBと衝突する。はねかえり係数をe とする。衝突後のA，Bの速度v₁'，v₂' を求め，衝突によって失われる力学的エネルギーを求めよ。

問76 なめらかな水平面上の一点Oに，質量mの小球が水平から角度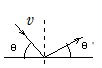θ下方に向けて速さvで衝突した。床とのはねかえり係数をeとする。

(1) 床への衝突直後の速さはいくらか。
(2) 衝突直後の小球の進む向きを求めよ。
(3) 衝突により小球が床から受けた力積を求めよ。

問77 なめらかな水平面上を速度Vですべっていた全質量(燃料も含む)Mのロケットが，質量mの燃料を瞬間的にロケットに対して後方に速さuで噴射した。

(1) 噴射直後のロケットと燃料の速度を求めよ。
(2) 同様な噴射が続き，(n−１)回繰り返された後のロケットの速度V_ｎを求めよ。

問78 床からの高さhの位置から小球を自由落下させた。床と小球とのはね返り係数をeとして，小球が止まるまでに移動した延べの距離Lと止まるまでの時間Tを求めよ。ただし，  (| x |＜1のときである)

問79 高さhの位置から小球Aを速度v₀で水平投射し，同時に小球Aから水平距離lで小球Aと同じ高さから小球Bを自由落下させたところ，小球A，Bは衝突した。衝突後の小球A，Bの速度を求めよ。ただし，小球A，Bともに質量が等しく，衝突は弾性衝突とする。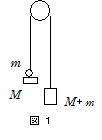

問80 図１のように，しっかり固定された表面がなめらかな円柱に，伸び縮みしない軽い糸を掛け，その一端に質量m＋Mのおもりをつるし、他の一端に質量mの球を乗せた質量Mの台をつるす。糸は球の中心を貫いてまっすぐにあけられた穴を通して台に結ばれている。
  また，台には球をはね上げる装置が備えてあり，その質量はMに含まれる。球ははね上げられた後，糸に沿って，摩擦なしに，鉛直方向に動くものとする。固定された円柱と糸の間にも摩擦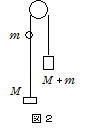はないものとする。
  静止している状態から装置を起動させ球を鉛直上方にはね上げる。このとき，球は短い時間内に重力に比べきわめて大きい力を受け，台はその反作用を受ける。台とおもりは糸で結びつけられているので，この間の糸の張力も大きな値になる。このことに注意して，はね上げられた直後の球の速さをW，台およびおもりの速さをV として両者の比を求めたい。運動量の変化に注目すれば，この間に球が台から受ける力積の大きさは[ 1 ]に等しく，おもりが糸から受ける力積の大きさは[ 2 ]に等しい。また，台は球と糸の両方から力積を受ける。したがって，　＝[ 3 ]････�@と求められる。球がはね上げられた後，台とおもりはそれぞれ等加速度運動をするが，その加速度の大きさは等しく[ 4 ]で向きは反対である。この間の糸の張力は[ 5 ]である。
　つぎに，おもりと球が図2のように円柱にあたることなく最高点に達したとき，それぞれの初めの位置から上昇した高さをHおよびhとして両者の比を求める。おもりが最高点に達したときの台とおもりの位置エネルギーの和が，はね上げた直後の台とおもりの力学的エネルギーの和に等しいことを用いれば，HはVを用いて[ 6 ]と表される。同様に考えてhはWを用いて[ 7 ]と表される。ここで，式�@を考慮すれば，比はm，Mを用いて[�G]と求められる。

問81 なめらかな水平床面上に置かれた板の中央に，細い鉛直の棒が固定して立てられている。棒の上端に，棒の長さより短い長さl の伸び縮みしない糸の一端に結ばれ，糸の他端に質量mの小さなおもりがつけられている。板と棒を合わせた支持台の全質量はM であり，糸の質量は無視できる。最初，支持台を静止した状態で，糸を張ったまま，おもりをθ＝0からθ＝θ₀の角度まで引き上げ，静かに放す。おもりと棒との衝突の際のはねかえり係数をeとする。板は常に床面から離れないとし，おもりは同一鉛直面内で運動するものとする。

(1) 鉛直線とθ₀をなす角度までおもりを引き上げた際に，おもりが得たポテンシャルエネルギーU₀はいくらか。
(2) おもりが棒に最初に衝突する直前の，水平な床面に対するおもりの速度v₁と支持台の速度v₂を求めよ。
(3) この衝突直後の，水平な床面に対するおもりの速度v₁' と支持台の速度v₂' をv₁，v₂の関数として表せ。
(4) 支持台とおもりのエネルギーの合計が，この衝突の前後でどれだけ変化したかを求めよ。
(5) おもりと棒との最初の衝突後，おもりが上昇し最高の位置に達したときの糸と棒のなす角度θ₁は
　　　　　    
を満足する事を示せ。

問82 質量Mの台がなめらかな水平面上にある。この台の水平部分の上にばね定数がkで質量が無視できるばねが置かれ，その左端を台に結びつけられている。台の右の部分はゆるやかな坂になっていて右端が最も高く，頂上付近は水平で台の水平部分からの高さはhである。
 　いま，両手を使ってばねを自然の長さからxだけ静かに押し縮め，ばねの先端に質量mの小さな物体Ｐを置き，すべてが静止している状態で同時に手を離した。すると物体Pはばねが自然長に戻ったところでばねから離れ，台の水平部分を通過し，坂を上がって台の右端から水平に飛び出した。重力加速度の大きさをgとし，台とＰの間，台と水平面との間に摩擦はないものとする。

(1)物体Ｐがばねを離れた瞬間の，物体と台の運動エネルギーを求めよ。
(2) (1)で，台の質量Mを一定に保って物体Ｐの質量mを変化させたとき，Ｐと台の運動エネルギーを，縦軸に運動エネルギー，横軸にをとり図示せよ。Ｐの運動エネルギーを実線で，台の運動エネルギーを破線で示せ。

問83 図のように質量mの小球Ａを長さl の糸で点Ｏにつるし，板Ｂをその左側の面が紙面に垂直で点Ｏの直下になるように台車に固定した。さらに床との固定を外して，台車が左右になめらかに動くようにした。板を加えた台車の質量はMであった。台車を静止させて小球Ａをもち，糸がたわまないように，また張力が加わらないようにして，紙面内で90ﾟ傾けて静かに放した。

(1) 小球Ａが板Ｂに衝突する直前における小球の速度V_Aおよび台車の速度V_Kを求めよ。
(2) 小球Ａと板Ｂとが弾性衝突するとき，衝突した直後の小球の速度W_Aおよび台車の速度W_Kを求めよ。ここでV_A，V_K，W_A，W_K は床に対する速度とする。また，板Ｂは変形せず，台車は傾かないものとする。さらに，質量Mは小球の質量を含まないものとする。

問84 図のように，ばね(自然長l₀，ばね定数k )の両端に質量mの小球ＡとＢが固定され，なめらかな水平面上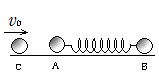に静止して置かれている。これに，質量mの小球Cが，BAの延長線に沿って速さv₀でAに弾性衝突した。次の問に答えよ。

(1) 衝突直後のＡとＣの速さはそれぞれいくらか。
(2) 衝突後の任意の時刻におけるAとBの距離をl とすると，AとBの加速度はそれぞれいくらか。ただし，加速度は右向きを正とする。
(3) (2)で求めた結果より，AとBの加速度の和は0になることがわかる。これは，AとBとの重心(すなわち中点)は等速度運動をしていることを意味する。その速さはいくらか。また，重心に質量が集中したと考えたときの運動エネルギーはいくらか。
(4) (3)でAとBの重心の運動がわかったので，次に重心とともに動いて観測すると，AとBは，重心に関して対称な単振動をしている。ところで(3)で求めた運動エネルギーは，衝突前のCの運動エネルギーより小さい。このエネルギーの減少は，AとBとの振動のエネルギーになったと考えられる。この振動のエネルギーはいくらか。また，AB間の最小距離を最大距離はそれぞれいくらか。
(5)　(3)と(4)の結果より，水平面に固定された静止座標系から見たAとBの速度を時刻 t の関数として表せ。ただし，CがAに衝突した時刻をt＝0とし，速度は右向きを正とする。

解答

ホーム  メニュー            序論･物理量  ベクトルとスカラー   落体の運動    力    運動の法則  円運動  仕事とエネルギー  運動量
           Top