問題解答                戻る

問75 運動量保存の法則から m₁v₁＝m₁v₁'＋m₂v₂'
　　　　はねかえり係数の式から
　　　　両式から m₁v₁＝m₁v₁'＋m₂(ev₁＋v₁')
　　　　　　　∴   
　　　　m₁＝m₂でe＝1の場合，v₁'＝0，v₂'＝v₁ つまり速さが入れ替わる。
　　　　力学的エネルギー保存の変化量��Eは
　　　　　　　
　　　　{   }内がm₁，m₂，eによってきまる変化量の係数である。
　　　　e＝1の場合��E＝0で(完全)弾性衝突である。
　　　　e＝0の場合��Eが最大で完全非弾性衝突である。

問76 (1) 衝突前の速度の水平，鉛直成分は，それぞれ　v_x＝v cosθ，v_y＝v sinθ
　　　　　　衝突後の速度の水平，鉛直成分は，それぞれ
　　　　 　　　　 v_x'＝v cosθ，v_y'＝−e･vsinθ
　　　　　　よって，衝突後の速さv'は
　　　(2)     ∴　tanθ のe 倍を満たす向き
　　　(3) 床に平行な方向はなめらかと考えるので，力積＝0，鉛直方向は上向きを正として，運動量変化は小球に与えられた力積に等しいから
　　　　　　　　　m{ evsinθ−(−v sinθ )}＝(e＋１)mv sinθ＞0
　　　　　大きさは(e＋１)mv sinθ で上向き

問77 (1) 分裂後のロケット，燃料の速度をそれぞれV_１，v'とすると，運動量保存の法則から
　　　　　　　　　MV＝(M−m）V_１＋mv'
　　　　　ロケットに対する燃料の相対速度が後方にuだから　　v'−V₁＝−u ← (u の負号に注意)
　　　　　両式から  
　　　　　　　MV＝(M−m)V₁＋m(V_１−u)＝MV₁−mu
　　　　　　　　
　　　(2) ２回目には(1)のMを(M−m)に書き換えればいいから  
　　　　　同様にして，n回目の噴射後の速度V_nは
        V₁，V₂，････，V_nのn個の辺々を加えて
                 

問78 １回目に床に衝突してからの最高点の高さをh₁，2回目に床に衝突してからの最高点の高さをh₂，以下同様にh₃，h₄，･･･h_nとする。
　　　　例１ から，h₁＝e²h，h₂＝e²h₁＝e⁴h，h³＝e²h₂＝e⁶h，･･･，h_n＝e²ⁿ･h
　　　　止まるまでに移動した距離Lは(変位ではない)，
　　　　L＝h＋2(h₁＋h₂＋h₃･･･h_n)＝h＋2(e²h＋e⁴h＋e⁶h＋･･･e²ⁿ･h)
　　　　　＝h{1＋2(e²＋e⁴＋e⁶＋･･･＋e²ⁿ)}＝h{1＋2e²(1＋e²＋e⁴＋･･･＋eⁿ)}
　　　　　＝ ← 与式で  x ⇔ とする
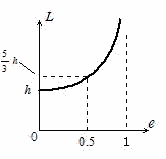
　　　　一方，止まるまでの時間T は
　　　　１回目に床に衝突するまでの時間t は
　　　　１回目の衝突から２回目までの時間t₁は
　　　　2回目の衝突から3回目までの時間t₂は
　　　　よってTは

問79 鉛直下方，水平右向きを正とする。衝突までの時間tは l＝v₀t      ∴   
　　　衝突直前の小球Aの水平，鉛直方向の速さv_Ax，v_Ayは，v_Ax＝v₀，v_Ay＝gt＝
　　　小球Bの水平，鉛直方向の速さv_Bx，v_Byは，v_Bx＝0，v_By＝gt＝
　　　水平方向について運動量保存の法則から
　　　　　　　mv₀＝m(v_Ax'＋v_Bx') ∴ v₀＝v_Ax'＋v_Bx'
　　　はねかえり係数の式から
               
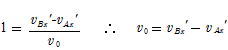
　　　両式から v_Ax'＝0，v_Bx'＝v₀
　　　この結果から衝突後小球A，Bは速度を入れ替えることがわかる。

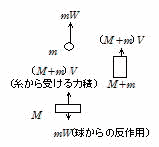
問80 �@�A 球が打ち上げられると台は下向き，右側のおもりは上向きに動き出す。物体の運動量変化は物体に加えられた
           力積に等しいから球が受けた力積は  mW (上向き)，
    　　　おもりが受けた力積は   (M＋m)V(上向き)
　　　�B 球,台,おもりはそれぞれ左図の力積を受ける。
　　　    台について，運動量変化＝台が受けた力積
　　　　　　　MV＝mW−(M＋m)V      ∴　       
      �C おもり，台それぞれについて運動方程式をたてると(糸の張力をT，加速度をαとする)
　　　　　　　(M＋m)α＝(M＋m)g−T，Mα＝T−Mg
　　　　両式より
　　 �D これより T＝M(α＋g)＝
　　 �E おもりが初速度V で距離H上がれば，台は下向きに初速度V で距離Hだけ落下する。最高点とはね上げ直
　　　　後の位置で，台･おもり系での力学的エネルギー保存の法則から
　　　　　　　
　　 �F上と同じくして，球についても
　　　　　 mgh＝mW²      ∴　 
　　 �G   

問81 (1) U₂＝mgl(1−cosθ₀)
　　　(2) おもり･糸･台系には衝突前後で外力が働かないから，運動量が保存される(この値ははじめ動いてないから
　　　　　0である)。また，おもりと棒が衝突するまでは，力学的エネルギーは保存されている。左向きを正の向きにす
　　　　　ると
　　　　　　　　mv₁＋Mv₂＝0 ･････�@
　　　　　　　　  ･･･�A
　　　　　�@からv₂＝　これを�Aに代入して
　　　　　　　　　，
　　　　　　(v_１＞0，v₂＜0から，おもりは左向き ，棒･台は右向きに動く)
　　　(3) 運動量保存の法則，はねかえり係数の式から
　　　　　　mv₁ '＋Mv₂'＝0 ･････�B，　 ････�C
　　　　　　両式から
　　　　　　(1)より v₁−v₂＞0 なのでv₁'＜0 (右向き)，v₂'＞0 (左向き)      
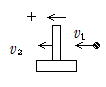
        (4)
　　　　　　　  
　　　 (5) おもりが最高点に達すると台も止まる。(∵　全運動量＝0)
　　　　　　　mgl (１−cosθ₁)＝e²mgl(1−cosθ₀)
　　　　　　　
　　　　　　　　(  )
問82 (1) P，台の速度をそれぞれv，V とすると，運動量保存の法則から
                mv＋MV＝0
　　　　力学的エネルギー保存の法則から
　　　　　　　
　　　　両式から
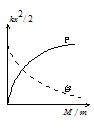
　　　　　物体の運動エネルギー  
　　　　　台の運動エネルギー      
　　　 (2)右図

問83 (1) 水平方向の運動量は，はじめ0でこの値は保存されるから
　　　　　　mV_A＋MV_K＝０･････�@
　　　　　力学的エネルギー保存の法則から
　　　　　�@式から
　　　　　これを�A式に代入して
　　　　　　　　
                 
　　　 (2) 運動量保存の法則から
　　　　　　　　
　　　　　　はねかえり係数の式から
　　　　　　　　
　　　　　　�B，�C式から
　　　　　　これと(1)から
　　　　　　　　

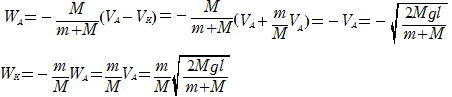
問84 (1)ＣがＡに衝突した直後は，ばねが縮んでないからAはばねから力を受けない。衝突前後でAとCの運動量は保存されるから，衝突直後のAの右
　　　　　　向きの速さをv_A，Cの右向きの速さをv_Cとすると，運動量保存の法則とはねかえり係数の式から
　　　　　　　　
　　　　　　両式から　
　　　　　　( e＝１の衝突だからエネルギー保存の法則からも求められる)
　　　(2) l＞l₀とすると,ばねの力は縮む向きにk(l−l₀)だから,Ａは右向きにばねからk(l−l₀)の力を受け，Ｂは左向きに同じ大きさの力を受ける。A，Bは
           ばね以外から力を受けないので，A，Bの右向きの加速度をα_A，α_Bとすると，運動方程式は
　　　　　　　　
      (3) 衝突直後のAの右向きの速さは v₀，Bの速さは0だから，衝突直後の重心の速さはである。よって重心のエネルギーは
　　　　　　　　
      (4) 衝突は完全弾性衝突だから，衝突前後の並進運動のエネルギーの差
　　　　　　　　
　　　　　が振動のエネルギーになっている。ばねが縮みきったときには，Ａ，Ｂの速度は0だから振動のエネルギーはすべて弾性エネルギーになっている。この
　　　　　とき，Ａ，Ｂ間の距離をl_１とすると
　　　　　　　　
　　　　　複合は＋のときに最大距離，−のとき最小距離を示す。
　　　(5) ばねがx だけ伸びたとき，Ａ，Ｂはばねからkxの力を受ける。このとき，重心からはかったＡ，Ｂの位置はつり合い位置からだけ遠くなっている。
　　　　　ここで，kx＝2k･と書けるから重心からはかるとＡ，Ｂはそれぞれ自然の長さばね定数2k，質量mのばね振り子と考えることができる。このばね
　　　　  振り子の角振動数は
               
           Ａ，Ｂの重心に対する速度は
　　　　　 　　
　　　　　Ａ，Ｂの速度v_A，v_Ｂはt＝0でv_Ａ＝v₀，v_B＝0だから
               
　　　　

戻る