�z�[�� ���j���[ ![]() �Ód�E �R���f���T�[ ������H ���E �d���U�� ��
�Ód�E �R���f���T�[ ������H ���E �d���U�� ��
�y�P�U�z�d��(electric field)�Ɠd��(electric potential)
�@�@�ѓd
���̂���[��]�ɓd��(electric charge)��тт邱�ƁB���̂̏ꍇ�̓d�ׂ͎��R�d�q�ł���B�d�q���s�����Ă���ꍇ�����ɁC�ߏ�ɂȂ��Ă���ꍇ�����ɑѓd���Ă���Ƃ����B���C�d�C(frictional electricity)
�قȂ镨���Ԃ̖��C�ɂ��d�q�̈ړ����N�����Đ����錻�ہB���C�ɂ���ĕ������\�����镪�q�Ԃ̋������ڋ߂��C���x���㏸���邱�ƂɂȂ�C�d�q�̈ړ����N����ƍl�����邪�C���̋@�\�͖��炩�ɂȂ��ĂȂ��B�����̏ꍇ�C�d�q��D�������D��͎d����(�d�����̏ڍׂ́u���d���ʁv�̍��Q��)���W���Ă���ƍl�����邪�C�s���̂ł͎d�����͌��߂��Ȃ��B�����q(�A�N�����C�����r�j�[���C�|���G�`�����Ȃ�)�͍���̕��q���s�K���ɗ��ݍ����č\������Ă��ēd�q����������͈͂�l�ł͂Ȃ��B
�K���X�Ȃǂ͓d�q���D���₷���B�Y�f���q�𒆐S�ɋ��L�����Ő��藧���Ă��镨��(�|���G�`�����C�e�t�����Ȃ�)�͓d�q��D���ɂ������ɑѓd���₷���B�����̏ꍇ�C�Q��̕����Ԃł̖��C�œd�q�̈ړ����N����ƁC�d�q��D���������̕����G�l���M�[���Ⴍ�Ȃ邪�C���q�ɂ���Ă��܂�d�q�̏�Ԃ��C�d�q����荞��ŒႢ�G�l���M�[��Ԃ����ꍇ�C�s���͓̂d�q���W�߂₷���B
�َ�̋�����(���C�����Ȃ�)�ڐG������ƁC���R�d�q�̈ړ����N����C�ڐG�d�ʍ���������B����͋����ɂ���ĕ��t��ԂŎ��R�d�q�̂��ő�G�l���M�[���قȂ邽�߂ƍl������B
���C�ɂ���Ăǂ��炪�����ɑѓd���邩��\�ɂ������̂��ѓd���ł���B�ѓd��̍����ɂ��镨�������C�E�ɂ��镨�������ɑѓd����B
�Ⴆ�C�є�ƃG�{�i�C�g�ł͖є炪���C�G�{�i�C�g�����ɑѓd����B�G�{�i�C�g�ƃ|���X�`�����ł̓G�{�i�C�g�����C�|���X�`���������ɑѓd����B�܂�C����ɂ���Đ������قȂ�B�܂������̕\�ʂ̏�Ԃɂ���ĈقȂ�B
�� �� �� ��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�є� ���� �t�����g�K���X �� �� ���� �G�{�i�C�g �|���X�`����
(�E�}�̓o���f�O���t�Ód�����������u �x���g����]�������C�d�C���N�������u�B�����{���g����������)
���̥�����d�ׂ̈ړ����e�Ղȕ����B��F����(�דd���q�͎��R�d�q)�C�d�����n�t(�דd���q�͐����̃C�I��)�Ód�C��
�s����(�≏��)����d�ׂ̈ړ����e�ՂłȂ������B��F�G�{�i�C�g�C����
�d�ׂ͐�����̂Q�킵�����݂��Ȃ����C����̓d�ׂ͐˗́C�َ�̓d�ׂ͈��͂������B�܂��C�ѓd�̂̓d�ׂ̑傫��|Q|�́C�d�C�f��(�d�q�P�̓d�� e��1.6�~10-19)�̑傫��|e|�̐����{�ł���B |Q|��|e|�~n (n�F�d�q��)���P�ȐÓd�C�͂̎���
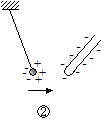
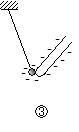
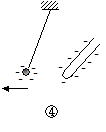
�G�{�i�C�g�Ɩє�C������ƁC�є炪���C�G�{�i�C�g�����ɑѓd����(�����})�B��]�ł���~����ɃG�{�i�C�g��u���C���̑ѓd�̂��߂Â���Ɛ˗͂�������]����(�����})�B�є���߂Â����ꍇ���������ĉ�]����(���E�})�B�P�U�|�P �Ód�U��(electrostatic induction)
�@�@�@�@�@�@�@�@�@
���̋��ɐ��̑ѓd�̂��߂Â���Ƒѓd�̂ɋ߂����Ɉَ�̕��d�ׁC�������ɓ���̐��̓d�ׂ�������B���ꂪ�Ód�U���ł���B���̒��̎��R�d�q�����̑ѓd�̂�����͂��Ĉړ��������ʁC�d�ׂ������ꂽ���߂ł���B�����d��̏ꍇ�����l�ɐ��̑ѓd�̂��߂Â���ƁC�߂����̋����ɑѓd�̂Ƃَ͈�̕��d�ׁC�������̔��ɂ͓���̐��d�ׂ�������B���͐��d�ׂǂ����ɂ��˗͂ɂ���ĊJ���B
�d�C�U��q�̎���
| |
 |
 |
 |
| �ѓd���ĂȂ����̋���≏���ł艺���� | ���̑ѓd�̂��߂Â���Ƒѓd�̑������C���Α������ɑѓd���C�ѓd�������d�ׂƕ��̑ѓd�̂��������� | �ڐG������ƕ��̑ѓd�̂̓d�ׂ����̋��Ɉڂ��� | ���̓d�ׂǂ����Ő˗͂��������������� |
��(�͂�)���d����g��������
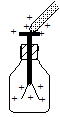
���̑ѓd�̂��g���Ă͂����d��S�̂𐳂ɑѓd��������@
| |
 |
 |
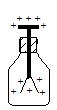 |
| �����d��͏�̋����ɁC�����ɔ��������������_����t���Ă���B�d�ׂ�����ƁC���ɂ��铯��d�ׂ̐˗͂ŊJ�� | ���̑ѓd�̂��߂Â���ƁC�Ód�U���ɂ���āC�����͕��C���͐��ɑѓd���� | ���̑ѓd�̂������ɐڐG������Ɛ��d�ׂ��ړ����C�����d��S�̂����ɑѓd���� | ���̑ѓd�̂��������Ă������d��͈�l�ɐ��ɑѓd���� |
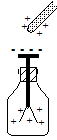
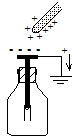
���̑ѓd�̂��g���Ă͂����d��S�̂ɑѓd��������@
 |
 |
 |
 |
| ���̑ѓd�̂��߂Â���ƁC�Ód�U���ɂ���āC�����͕��C���͐��ɑѓd���� | ������ڒn(�A�[�X)����Ƒѓd�̂�艓�����̐��d�ׂ��n���Ɉړ����邪�C�����㕉�d�ׂ͑ѓd�̂̐��d�ׂɈ��������Ă��Ĉړ��ł��Ȃ� | �ڒn���O���Ă����̊J���͂��̂܂܁B�����̕��d�ׂ́C�ѓd�̂̐��d�ׂɈ��������Ă���̂ňړ��ł��Ȃ� | ���̑ѓd�̂���������Ƌ����̕��d�ׂ����Ɉړ����C�����d��S�̂����d�ׂɑѓd���� |
�t�@���f�[�̕X���̎���(1834�N)
 |
 |
 |
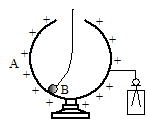 |
| �@A�͌��ׂ̍������e��Ő≏�̂Ŏx������Ă��� | �A���̑ѓd��B��e����ɓ����ƐÓd�U���ɂ���ėe��̊O�������C���������ɑѓd����BB�𒆂ňړ������Ă����̊J���͕ς��Ȃ��B | �BB�����o���Ɣ��͕��� | �CB��e��̓��ʂɐڂ���ƁC�a�̐��d�ׂƗe����ʂ̕��d�ׂ����E���C�O�����������ɑѓd�����͊J�� |
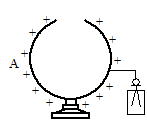 |
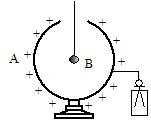 |
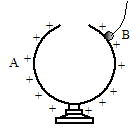 |
 |
| �DB����苎��ƑS�̂����ɑѓd�����͊J���Ă��� | �E �D�̏�ԂŁC�ѓd���ĂȂ�B��e��̒��ɓ���Ă�B�͑ѓd���Ȃ� | �F�ѓd���ĂȂ�B��e��̊O�ɐڐG������ƁCB�͐��ɑѓd���� | �GB�𔓌��d��ɐڂ���ƑS�̂����ɑѓd�������J�� |
�P�U�|�Q �U�d����(dielectric polarization)
�s����(�≏�́C�U�d��)�ɏ�L�Ɠ��l�ɐ��̑ѓd�̂��߂Â���ƁC�ѓd�̂ɋ߂����Ɉَ�̕��d�ׁC�������ɓ���̐��̓d�ׂ�������B�����̓d�ׂ�����邱�Ƃ́C���̂ɋN����Ód�U���Ɠ��������C�������قȂ�B�s���̂̏ꍇ�C���R�d�q�̈ړ����Ȃ�����ɁC���q���̓d�q�̂���ɂ���ēd�ׂɕ肪�����邱�Ƃ������ł���B���̏ꍇ�̓d�ׂ����ɓd��(polarization charge)�Ƃ����B�����̂悤�ȓ��̂̏ꍇ�́C�d�E�ɂ���Ď��R�ɓ����鎩�R�d�q�̂悤�ȓd�ׂ�^�d�ׂƂ������C�s���̂̏ꍇ�͓d�q�͂��ꂪ������X�̌��q���邢�͕��q���痣��邱�Ƃ��ł����ʒu����������邱�Ƃ������������̂ł��̂悤�ȓd�ׂ𑩔��d�ׂƂ����B
�@�d�E���Ȃ��ꍇ�s���̂ɓd�ׂ�����Ȃ� �@�@�@�@�@ �d�E���ɂ���ƕs���̕\�ʂɓd�ׂ������
�@�@�@�Ód�U���ƗU�d���ɂ̔�r
�Ód�U�� �U�d���� �ގ��_ �d�ׂ̌�����d�ׂ̌���� ����_ ���̂ɋN���� �s���̂ɋN���� �d�ׂ��ł��� �d�ׂ��ł��Ȃ� �^�d�� �����d��
�P�U�|�R �Ód�C�Ɋւ����N�[�����̖@��(Coulomb's law)
�N�[�����ɂ���Ĕ������ꂽ�d�Ԃɓ����͂ɂ��Ă̎������͍��}�̂悤�Ȃ˂��ꔉ�ɂ���čs��ꂽ�B�d�ׂ�^�������ɍׂ��≏���ł�ꂽ�_�Ɖ��̗e��̂ӂ��̕����Ɏ��t����ꂽ������̓d�ׂ�p�ӂ���B�e��ɂ̓��������U���C�����_����]����p�x�ɂ���ēd�Ԃ̗͂̑傫��������ł���B���̌��ʁC�d��q1�Cq2�C�݂��̋�����r�Ƃ���ƁC
(16-1)
�ł������Bk�͎��̂悤�Ɍ��߂���B
SI�P�ʌn (MKSA�P�ʌn)
�^�ŁCr��1m�Ƃ��C���ʂ̓d�Ԃɓ����͂̑傫����F��N �ɂȂ�悤�ȓd�ׂ�1C(�N�[����)�ƒ�߂�B��0�͐^�̗U�d������0��
��8.854�~10-12[F/m] F�̓t�@���b�h�B�t�@���b�h�ƗU�d���ɂ��Ă̓R���f���T�[�̍��Q�Ƃ̂��ƁB
�܂�C�ł���B�U�d���� �̕������ł̃N�[�����̖@����
[N] �ł���B
������x�N�g���\������ƁC(
�͒P�ʃx�N�g���ł���)
CGS�Ód�P�ʌn(CGS esu) esu��electric static unit
���ݎg���ĂȂ����C���̂悤�Ɍ��߂��Ă���B
�^��r��1cm�Ƃ��C���ʂ̓d�Ԃɓ����͂̑傫����F��1dyn(�_�C����g�cm/s2)�ł���悤�ȓd�ׂ�1CGSesu(��[C])�ƒ�߂�B
�܂�Ck��1�Ƃ���P�ʌn�ł���̂ŁC�N�[�����̖@����[dyn]�ł���B
������1.0�~10-2Kg�C�d��qA=3.5�~10-7C�̓d�ׂ�������A��V�䂩�玅�ł艺���C�d��qB�̓d�ׂ̏���B�Ƃ������ɂ�����C���� A�CB�͈���������0.30m�̋����ŏ���A�͉�����30߂̊p�x��ۂ��ĐÎ~�����B�d�͉����x��9.8m/s2�Ƃ���B
�܂�k��9�~109[N�m2/C2]�Ƃ���B
�@(1) ����A������B����Ă���Ód�C�͂͂����炩�B
�@(2) �d��qB�͂����炩�B
(3) ���̌�C����A�CB��ڐG�������B����A�CB�̑傫���͓������Ƃ���B
��(1) ����A�ɓ����͂͋��߂��F�C�d�́C���̒��͂ł����͂荇���Ă���B���}���F/mg��tan30߂�����
F ��mgtan30߁�1.0�~10-2�~9.8�~��5.7�~10-2N
(2) �N�[�����͂̎�����
F��9�~109�~��5.7�~10-2
����������C���͂����� qB���|1.6�~10-6C
(3) ����A�CB��ڐG������ƁC�d�ׂ͏���A�CB�̕\�ʐςɔ�Ⴕ�ĕ��z�����B�ڐG��̑��d�ׂ�
�@�@ q��qA�{qB��(+3.5�|1.6)�~10-6���|1.25�~10-6���|1.3�~10-6
����A�CB�̑傫���͓������̂œ�������邩��CqA'��qB'���|1.25�~10-6/2���|6.3�~10-7C
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���a��1�Fn �Ȃ� qA'�FqB'���P�Fn2�ɕ��z�����B
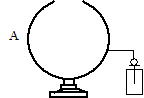
�P�U�|�S �d��(electric field) ��� �d�E�Ƃ�����
��ʂɓd�ׂ��Ód�C�͂����Ԃ�d��Ƃ����B�d��E�́C�d��q[C]����F[N]����Ƃ���
(N/C) (16-2)
�ŗ^�����x�N�g���ł���B
�_�d��q[C]������r [m]�̈ʒu�ō��d��E��
����r �̈ʒu�ɓd��q ' ��u���ƃN�[����������B���̗͂�16-2����F �Ɠ���������
(N/C) (16-3)
������x�N�g���\������ƁC(
�͒P�ʃx�N�g���ł���)
�܂��C�d��̌����́C���̓d�ׂ���͂̌����ƒ�߂�B
�d�C�͐�
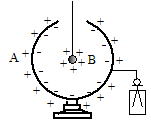
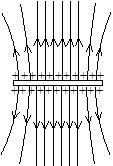
�d�E���ɒu���ꂽ���̓_�d��(����������d�ׂƂ�Ԃ��Ƃ�����)�̎�͂�A�����ĕ`�����}�ŁC�d�C�͐���
�@ ���d�ׂ���o�ĕ��̓d�ׂɓ���r���ŏ����Ȃ�
�A �d����̊e�_�̐ڐ��́C���̈ʒu�̓d��̌���������
�B ���������}�����ꂵ�Ȃ�
�C �݂��ɔ����������C�k�����Ƃ���
�D �d��̋����ꏊ�ł͖��ɁC�ア�ꏊ�ł͑a(�܂�)��ɂȂ�
�Ƃ��������������Ă���C�d�C�͐�������Ɠd��̗l�q���킩��B�d�C�͐��̖{���́C�d�E��E[N/C]�̈ʒu�ŁC�d�E�ɐ����ȒP�ʖʐϓ�����E[�{]�������̂Ƃ���B
| �d�C�͐��̗� | ||
�@�@�@�@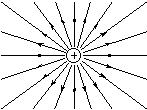 �@�@�@�@ �@�@�@�@ |
�@�@�@�@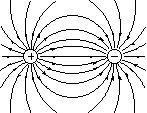 �@�@�@�@ �@�@�@�@ |
�@�@�@�@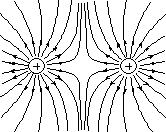 �@�@�@�@ �@�@�@�@ |
| �_�d�� | �����̓_�d�� | ���̓_�d�ב� |
 |
 |
|
| ���̕��ѓd�� | ���s�R���f���T�[ | |
�����ɂ��d�C�͐� ���̓_�d�� �����̓_�d�� ����̓_�d�� �Ód�Օ�(�����ɓd�C�͐��Ȃ�) ���s�� �n�T�~(�𗋐j��͂�)
�K�E�X�̖@��
�u�C�ӂ̕Ȗʓ�����o��(����)�d�C�͐��̑��{���́C�Ȗʓ��̑��d��Q��4��k(������4��k��1/��)�{�ł���v�B
�L����̂���ѓd�̂����d�E E �����߂邽�߂ɗL���ł���B
�� ����l�ȏꍇ�C4��k��1/�� ������C�d��ƕȖʂ��������Ă���Γd�C�͐��̖{����
�ł���B
�d������߂�菇
�@ �d�ׂ��܂ޕȖʂ��l����(�Ώ̐��̂��鋅�C�����̂Ȃ�)
�A �Ȗʓ��̑��d��Q�����߂�
�B �Ȗʂ���o��(����)�d�C�͐��̑��{��N��4��k�����߂�
�C �Ȗʂ̕\�ʐ�S�����߂�
�D �d���E��N/S�ŋ��߂�
�ѓd�̂̍��d��̗�
���̋�
���d��Q[C]����l�ɕ\�ʂɑѓd�������aa[m]�̓��̋�����鋅�̒��S���狗�� r
�Ƃ���B
�@r��a �ł́C�d�ׂ����݂��Ȃ�����d�E�͂Ȃ��B
r��a �ł́C�ȖʂƂ��Ĕ��ar �̋����l����B
�@�\�ʐ�S ��4��r2[m2]�B���̒��̑��d�ׂ�Q[C]������C
���̕Ȗʂ���ł�d�C�͐��̑��{��N��4��kQ[�{]�ł���B����āC�d�EE ��
E��(�_�d�ׂ̍��d��Ɠ����ł���)
�����Ɉ�l�ɑѓd������ ���d�ׂ�Q�C���̔��a��a[m]�Ƃ���B
r��a�F�d�ז��x�����Ƃ���Ƒ��d��Q��������C�����̓d�ׂ�
�@�@�@�@�Ȃ̂ŁC�d�C�͐�������N��N��4��k�C�d�C�͐��̂ł�\�ʐ�S��S��4��r2
�d���E��N/S��4��k/4��r2��
��
�@�@�@�@�@�@�@�@�� E�� r �͖��L���͂Ɠ��`�ł���B
�@�@�@�@�@�@�@�@�@�@�@�@r��a�F���̋��̏ꍇ�Ɠ����ɂȂ�B��
�����ɒ������̖_ �d�ז��x����(C/m)�Ƃ���B
���̓��� E��0
������̋���r �̓��O(����l �̕������l����)
N��4��k�(��l )�CS��2��r�l
E����
��
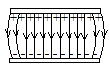
�����ɍL�����̕��ʔ�(�n�\�̂悤�ȏꍇ)
�@ �\�ʓd����(C/m2) �Ƃ���B
���̂̓����ɓd�C�͐��͂Ȃ�����C�d�C�͐��͊O�Ɍ������ďo�邾���B�d�C�͐����o��ʐς�S��1m2�Ƃ����
N��4��k�(���~1)��4��k��
E����4��k��/1��
�܂�C�����ɍL���ѓd�̂ƁC�d��͖ʂɐ����ő傫���͋����ɂ��Ȃ��B
�������C���ʂɑѓd���Ă���ꍇ�́CE��
�P�U�|�T �d��(electric potential)�Ƃ�
�Ód�ꒆ�œd�ׂ��ړ�������̂ɗv����d���́C�O��̈ʒu�����ɊW���C���̌o�H�ɂ͖��W�ł���B�܂�d�C�͕͂ۑ��͂ł���B�d����̊�_B���瑼�̓_A�܂Ő��̓d�ׂ��ړ�������Ƃ��C�d�C�͂ɍR���đ�����d�������Ă��Ȃ���Ȃ�Ȃ��ꍇ�CA��B���d�ʂ������Ƃ����B���ɓd�C�͂��d��������ꍇA��B���d�ʂ��Ⴂ�Ƃ����B
�u�ѓd�̂��狗�� r �ł̓_�o�̓d�ʂ́C��_(������)���琳�̓_�d�ׂ�d�E�ɋt����Ă������Ƃo�_�܂ňړ�������̂ɗv����O�͂̂���d���v�B�܂��́C�u�o�_���琳�̓_�d�ׂ���_�܂ňړ�������̂ɕK�v�ȓd��̂���d���v�ƒ�`����B
�_�d��Q���狗��r�ł̓d�ʂ�V��
�@�@�@�@(16-4) �ł���B
1[C]�̓d�ׂ��ړ�������̂�V[J]�̎d�����K�v������q[C]�̓d�ׂ��ړ�������ɂ͂���q�{�̎d�����K�v�ɂȂ�C�d�ʍ�V�̂Q�_�Ԃ��ړ�������d��W��
�@�@�@�@W��qV (16-5) �ł���B
�@�d�ʂ̒P�ʂ́C1[V]��1[J/C]�ŁC1[C]�̓d�ׂ��ړ�������̂�1[J]�̎d�����K�v�ȂQ�_�Ԃ̓d�ʍ���1[V]�ł����B
�@ �d�ʂ̓X�J���[�ʂł���B�P��V(�{���g)���{���^����Ƃ��Ă���B
�d��Ɠd�ʍ��̊W
��l�ȓd��̏���
A�CB�_�Ԃ̓d�ʍ���V(V)�Ƃ���ƁCA�CB�Ԃɒu���ꂽ���̓_�d�ׂ��d�ꂩ���͂�F��qE(N)������
�Ód�C��(�d��)���d��q(C)������d(m)�ړ�������d��W (J)��
W��Fd��(qE)d��q�Ed��qV
�� Ed��V E��(V/m) (16-6) �� �d��́C�d�ʂ̋����ɂ��Ă̕ω��̊����ł���
��l�łȂ��d��̏ꍇ
�ŗ^������B(���������Ă���̂́C�d�ʂ�����������ɓd��̌��������邩��ł���)
�d�ʂ̗� (���ꂼ��̓d��E�͏�L�ѓd�̂̍��d�E���Q�Ƃ̂���)
�@ ���̓_�d��
r������V��0 �� C��0
��
�A �ѓd���̋�
r��a
r������V��0 �� C��0 ����
r��a ��E��0�������ň��
�B �����Ɉ�l�ɑѓd�������d�ז��x�����Ƃ���
r��a�F���̋��̏ꍇ�Ɠ������C
��
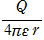
r��a�F���d��Q��������C�����̓d�ׂ�
�� E��
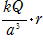
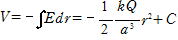
r��a�� �A��������(�� r��a)
�@�@�@�@�@�@�@�@�@�@�@�@ ����
�}���C
�C �����ɒ������̖_
E����
r������V��0�Ƃ���ƁC�_�̋ߖT(r��0)��V�����ƂȂ�̂ŁC�_�̔��a��a �Ƃ���ƁCr��a ��V��0�Ƃ���
C��2k��loga ��
�D �����ɍL�����̕��ʔ�(�n�\�̂悤�ȏꍇ)
E���C
���|4��k��r�{C
r��0��V��0 �Ƃ���ƁCC��0
�� V���|4��k��r���|
���ʂɑѓd����ꍇ�� V���|
�d�C�͐��Ɠ��d�ʐ�(��)�̊W
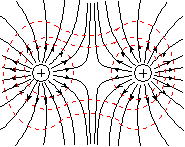
�d�ʂ̓������Ƃ��������łł�����(��)�d�ʐ�(��)�Ƃ����B
���d�ʐ�(��)�Ɠd�C�͐��݂͌��ɒ������Ă����B���}�Ŏ����͓d�C�͐�,�j���͓��d�ʐ��B
�d�C�͐��ɐ����ȕ����ɐÓd�C�͂̐������Ȃ����߂ł���(���d�ʖʂɉ����ēd�ׂ��ړ����Ă��d�C�I�ʒu�G�l���M�[�͕ω����Ȃ�)�B
�d�C�͐��Ɠ��d�ʖʂ̊W�̗�
�@�@�@
�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@
�P�U�|�U �d�ꒆ�̈ʒu�G�l���M�[
�d��͕ۑ��͏ꂾ����C�ʒu�G�l���M�[���l���邱�Ƃ��ł���B
���̂��Ƃ���C�_�d��Q���狗��r �̈ʒu�ɒu���ꂽ�d��q �̂��Ód�C�͂ɂ��ʒu�G�l���M�[ U��
�@�@�@�@ U��qV��q���
(16-7)
�ŁC�X�J���[�ʂł���B
�P�U�|�V �d�ꒆ�̎d��
�d�ꒆ�œd�ʍ���V[V]�ł���Q�_�ԂŁC�d�ʂ̒Ⴂ�ʒu���獂���ʒu�ɐ��̓d��q���������ړ������邽�߂ɊO�͂̂���d����W��qV ��0�C�d��̂���d����W���|qV �ł���B
�d�ꒆ�ŊO��(�Ód�C��)���d�����ړ����邽�߂ɂ���d���̐����́C�O��(�Ód�C��)�ƈړ������������ꍇ�ɐ��C�t�����̏ꍇ�C���ł���B
�O�͂̂���d����WF�C�Ód�C��(�d��)�̂���d����Wf�Ƃ���B
VA��VB�̏ꍇ
�d��q��0�ł�
B����A�Ɉړ�����ƁC WF��0�CWf��0 �ł���B
�d��q��0�ł�
WF��0�CWf��0 �ł���B
(VA��VB�̏ꍇWF�CWf�̕����͂��ꂼ���L�Ƌt�ɂȂ�B�܂��Cq��0�̏ꍇ��WF�CWf�̕����͂��ꂼ���L�Ƌt�ɂȂ�)
��
���̓_�d��q�����}��A��B��C��D��E��F�Ƃ������ړ�����Ƃ��C�O�͂̂���d���̕������ē�����B
�O�͂������Đ��̓d�ׂ��ړ�������Ƃ��C�d�ʂ̍������ֈړ��������ꍇ�����C���̋t�����C���d�ʊԂ�0�ł���B
���FA��B�CC��D
���FE��F
0 �FB��C�CD��E
�d�ꒆ���^������דd���q�̉^���G�l���M�[
����m�C���d��q�̓_�d�ׂ��d�ꂩ��Ód�C�͂���A����B�Ɉړ�����(vA��vB�Ƃ���)�B
A�ł̑�����v0�CB�ł̑�����v�Ƃ���Ƃ��C�^���G�l���M�[�̕ω��ʂ͓d�ꂪ�d�ׂɂ����d���ɓ���������
(q��0�̏ꍇ��B����A�Ɉړ�����)
�d����̓���
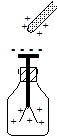
�d����ɓ��̂�u���ƁC���̓��̎��R�d�q�͊O���d��E�Ƌt�����̗͂��O���d��Ƌt�����̓d�EE ' ����������B
���R�d�q��E�{E '��0�ƂȂ�܂ňړ���������̂œ��̓��̓d���0�ł���B���������ē��̓��͓��d�ʂł���B
���̂��߁C���̂ɂ���Ĉ͂܂ꂽ���ɓd�C�͐������邱�Ƃ͂Ȃ��B���̂悤�Ȍ��ۂ��Ód�Օ��Ƃ����B���}�̂悤�ɋ��Ԃň͂܂ꂽ���ɔ����d������C�O�ɐ��̑ѓd�̂��߂Â���ƁC���Ԃ̏㕔�ɕ��̓d�ׁC���Ԃ̉����ɐ��̓d�ׂ��Ód�U���ɂ���Đ�����B�����ɂ��d��͐}�̉������Ɍ����������C���ꂪ�O���̑ѓd�̂ɂ��d��Ƒł����������̂Ŕ��͊J���Ȃ��B
�g���l���̒����邢�̓R���N���[�g�̌����̒��ɓd�g������ɂ����̂͂��̌��ۂ̂��߂ł���B�d�g�̉e��������邽�߂ɂ́C��������ԂȂǂŕ����ƗL���ł���B
�z�[�� ���j���[ �Ód�E �R���f���T�[ ������H ���E �d���U�� ��