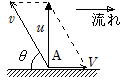
図の角度をθ とすると,
問5 船が川を往復するとき,図のAを出発して流れに直角に進むには,川の流速V と船の静水に対する速度vとの合速度uが流れに直角になるように船を進めればよい。
だから,往復するに要する時間t は
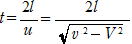
図の角度をθ とすると,を満たす向きに進めればよい。
問6 (1)川岸に対する船の速さは,上りではc- v,下りではc+ vだから 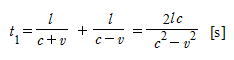
(2)水の速度と,水に対する船の速度のベクトル和が川岸に対する船の速度になるから,船の速度はである。
∴[s]
(3) (2)のt2を書き換えて∴ t1 >t2
問7 (1) 岸に対する水の速度をv(水),岸に対する船の速度をv(船)とすると,
水に対する船の速度v(水・船)はv(水・船)=v(船)-v(水)になる。
v(船)はA→Bの向きが決まっているからv(水・船)の大きさが最小になのは、PQをABに垂直に(PQ'の向き)にとったときである。
∴ ABに垂直に川上に向けて漕げばよい。
(2) このとき,|PQ'|=|v(水)|sinθ (θ はABと川岸のなす角度)=
問8 東向きを正の向きとすると,80-100=-20 ∴ 西向きに20[m/s]
問9 右図でOS'を真の風速u,OP1=v,OP2=2vを人の速さ,OS'を人がはじめに感じた風速,OS''を人の速さが2倍になったときに感じた風速とする。角OP2S'=45゚だから図より![]()
問10 (1) 風の速さは右図より v1=20.0,v2=15.0 ∴ ![]() =25.0[m/s]
=25.0[m/s]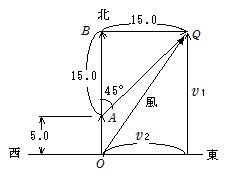
(2) (1)より
問11 (1) 自動車の x- t グラフは,原点を通る直線だから等速直線運動で,速さをv とすると
x= v t の関係から t=20,x=400だから v=20
∴ 速さ 20[m/s]の等速直線運動
(2) グラフは放物運動らしいので x=At 2 とすると,表より A=1であることがわかる。
∴ x= t 2になる。
このことから等加速度運動であることがわかるので x= v0t+Nα t 2=t 2 より α=2[m/s2]
(3) t=20[s]のときの電車の速さは v=2×20=40[m/s],自動車の速さは20[m/s]だから自動車の人が見た電車の相対速度は
40-20=20[m/s]である。(電車の速さはv=αt=2tだから 2t-20が一般式である)
問12 (1) 物体が速度vに達する時刻をt1,減速しはじめた時刻をt2とする。
v=αt1・・・・① ,0=v-β (T-t2)・・・・・②,
①から t1=v/α,t2=T-v/β
これを③に代入して
(2) Tを一定にして,l を最大にするには等速度運動の区間をなくせばよい。よって加速度α で最高速度vに達し,すぐに加速度βで減速し時刻Tに速度が0になるから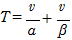
∴
このときの l は等速区間の時間は0
問13 列車の長さをl,加速度をα,先端から距離xでの速度をv とすると
(2) v22-v12=2αl ,v2-v12=2αx
両式からv <0 は不適
(1) x=l/2として
問14
(1) x方向:vx=4[m/s],y方向:vy=3[m/s]
∴=5 [m/s]
(2) 2~4[s]は加速度一定で,その大きさは
(3) x方向:グラフの面積から x=4×2+(4×2)/2=12[m]
y方向:グラフの面積から y=3×2+(3×2)/2=9[m]
∴ 求める距離lは=15[m]
(4) 0<t<2:等速運動 x=4t,y=3t
t を消去して, t=2で x=8,y=6
2<t <4:等加速度運動 x=8+4(t-2)-(4/2)・(t-2)2
y=6+3(t-2)-(3/2)・(t-2)2
t を消去してよって0<t <4 で直線の関係になる(右図)。
戻る