�z�[�� ���j���[ ![]() ���_������� �x�N�g���ƃX�J���[ ���̂̉^�� �� �^���̖@�� �~�^�� �d���ƃG�l���M�[ �^����
���_������� �x�N�g���ƃX�J���[ ���̂̉^�� �� �^���̖@�� �~�^�� �d���ƃG�l���M�[ �^����
�y�R�z �x�N�g��(vector)�ƃX�J���[(scalar)
�X�J���[(scalar)�����傫���݂̂��� �i�����C�����C�����C�d���C�G�l���M�[�C���ԁC���ʁC�d�ׁj
�x�N�g��(vector)�E�E�E�傫���C����(����)������ �i�ψʁC���x�C�����x�C�́C�^���ʁC�͐ρj
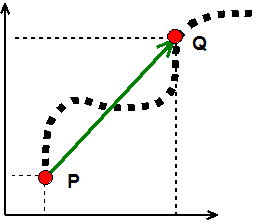
P�_����Q�_�܂ňړ������ꍇ
�ړ������͋Ȑ�(�_��)�̒��� ![]() �X�J���[
�X�J���[
�ψʂ͒���(����)�̌����ƒ��� ![]() �x�N�g��
�x�N�g��
�x�N�g���̐���
�x�N�g���\�L ![]() �C
�C![]() �̂悤�ɕ\�L����B
�̂悤�ɕ\�L����B
�@�@�x�N�g���̉��@ ![]() ��
��![]() �{
�{![]()
�@�@���@�̌��� ![]() �{
�{![]() ��
��![]() �{
�{![]()
�@�@���@�̌����� ![]() �{�i
�{�i![]() �{
�{![]() �j���i
�j���i![]() �{
�{![]() �j�{
�j�{![]()
�@�@�x�N�g���̌��@ ![]() �|
�|![]() ��
��![]() �{�i�|
�{�i�|![]() �j
�j

![]()
�x�N�g���̘a�́C��ʂɂ�C��A�{B �ł���B
�傫���� ![]()
���_(material point)�Ƃ́C���̂̑傫�������C�S���ʂ��P�_�ɏW�܂����ƍl����ƁC�戵���������ւ�ȒP�ɂȂ�B���̂悤�ȉ��z�̓_�����_�Ƃ����B
���̂̉^���͂P���_�̉^���ő�\�ł��C�����ɔ�ׂĕ��̂̑傫���������������ꍇ�i�f���^���Ȃǁj�͎��_�Ƃ݂Ȃ���B
����ɑ��āC�͂��Ă��ό`���Ȃ����z�I�ȕ��̂�����(rigid body)�Ƃ����B�����ɂ͑��݂��Ȃ����C�͊w�Ŏ戵�����ȒP�Ȃ̂ł��̂悤�ȕ��̂��l����B
�y�S�z �^����\���� �ʒu�x�N�g�� �C���x�C�����x
�� �^����\���ʂɁC�ʒu�i�ψʁj�C���x�C�����x�Ȃǂ�����B
�� �^���Ƃ͕��̂̈ʒu�����ԓI�ɕω����邱�Ƃł���B���̂̉^�����L�q���邽�߂ɂ́C�ʒu���W�Ǝ��Ԃ̊W��m�邱�Ƃ��K�v�B�܂��ʒu���W�̎��Ԃɑ���ω��̊����ł��鑬�x�C���x�̎��ԕω��̊����ł�������x�̎��Ԃɑ���ω��ׂ邱�Ƃ��K�v�ł���B
�S�|�P �ʒu�x�N�g��
���̂̈ʒu�́C���_O�����߁C��������̍��W��\���B
�������W�n���Ƃ�ꍇ
�ƕ\�����Ƃ��o����B
�ψ�(displacement)
�@�@�u�ψʁv�́C�u�ʒu���W�̕ω����v�������x�N�g���ł���B
�@�@�ψʃx�N�g���� �n�_�iP�_�j�ƏI�_�i�p�_�j�̈ʒu�x�N�g��
��
�̍��ɓ������B
�@�@�@�@
=
�|
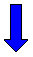
����(speed)�́C�ʒu�̎��ԓI�ω��̊���
���ς̑���(4-1)
�u�Ԃ̑���(4-2)
�E�}�Ň�t ����t3�C��t2 �C��t1�Ə���������x�| t �O���t�̌X���̑傫�������߁C��t ������Ȃ�����������ƁC
�@�@����t �ł́i�u�Ԃ́j���������߂邱�Ƃ��ł���B
���x�́C �ψʃx�N�g���̎��ԓI�ω��̊���
�@�@�����Ƒ��x�͈قȂ��B��������E�Ɉ��̊�����2[s]��1[m]�i�݁C
�@�@1[m]���ǂ�ꍇ�C
�@�@�@�@�@���ς̑�����(1�{1)�^2��1[m/s]�C���ϑ��x��(1�|1)�^2��0[m/s]
�S�|�Q ���x(velocity)
�@�@���x�́C �ψʃx�N�g��r �̎��ԓI�ω��̊���
�@�@�u�ԑ��x(4-3)
�@�@�u�ԑ��xv �� x�Cy ����������
���̂��߂ɓ����グ���ꍇ,��ɑ��x�̌����� �����͓�������,���x���ς��^���̗�
�ς���Ă����
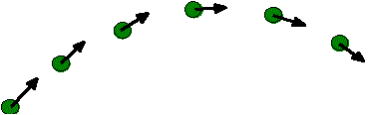
�S�|�R �����x(acceleration)
�@�@�����x�F ���x�x�N�g���̎��ԓI�ω��̊���
�@�@(���x�̑傫���𑬂��ƌĂԂ��C�����x�̑傫���ɓ��ʂȖ��O�͂Ȃ�)
�@�@�u�Ԃ̉����x(4-4)
�@�@�u�ԉ����xa ��x�Cy��������
�@�@���ς̉����x(4-5)
�@�@�@�@�@ �J�[�u���Ȃ���ꍇ�̉����x
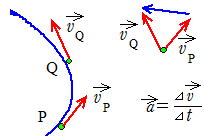
v�|t �O���t�̌X���������x
�S�|�S ���Α��x(relative velocity)
B�ɑ���`�̑��Α��xvBA(B���猩���`�̑��Α��x)��
vBA��vA�|vB (4-6) �ŗ^������B
���Α��x�́C(����̑��x)�|(��̑��x)
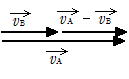

�|
�́{(�|
)����
�Ɋ�x�N�g��
���t�����ɉ����邱�ƂɂȂ邪�u�ڋʂ̕��@�v���ȒP
�@ �x�N�g���̎n�_�𑵂���
�A ��x�N�g���̖�Ɂu�ڋʁv�����C
�u�ڋʁv���瑊��̃x�N�g���̖�Ɍ����ăx�N�g�������B ���ꂪ�|
�ł���B
��1 ���̂Ȃ����ɑ���v�ʼn��������Ɍ������č~��J���C�����xV �Ő����ɓ����d�Ԃ̒����猩�����Α��x�̑傫���C���������߂�B
�� ���xv�CV �̎n�_�𑵂���V �̖��v �̖��Ɍ����ĕ`�����x�N�g�����C�d�Ԃ̒����猩�����Α��x�ł���B
���̑傫���́C���̌����́C�}�̊p�x���� �Ƃ���Ƃ����B
��2 ���������Ɉ��̑���v �Ői�ދC�����珬�����C���ɑ��ĉ�������ɑ���v0�œ���������(�����グ������C���͐����ɓ����Ă���)�B�n��ŐÎ~�����lA�������O�ՁC�C���̒��̐lB�������O�Ղ�`���B
�� �n��̐Î~�����lA������������Ɛ�����v�C���������v0�œ����o���̂Ŏߏ���ւ̓����グ�^��(�����^��)�C�C���̒��̐l�a������Ɛl�a����ɐ��������֑���v0�œ����Ă��邩��C���������ɂ͓���������������v0�œ����グ���^���Ɍ�����B
�ψʁC���x�C�����x�̑���� ���l�Ԃ̕��s��
�S�|�T �P�����̉^��
�@�������x�����^��
�����x��
�@�@�ŗ^������B
�@�@ t1��0�Ct2��t�Cv1��v0�Cv2��v �Ƃ����
�@�@�ł���B�� v�|t �O���t�̌X���������x
�@�@���������������v��v0�{at (4-7) �� ���}�@
�@�@ t1��0 �̂Ƃ�x1��x0�Ƃ����
�@�@�� v�|t �O���t�̖ʐς��ψ�(*1�Q��)
�@�@�����(4-1)��������
�@�@(4-8) �� ���}�A
�@�@(4-7)���������(4-8)����
�@�@(4-9) �� ���}�B
�@�@a��0 �̏ꍇ�̃O���t
�@�@a��0 �̏ꍇ�͓��������^��(�����x�^��)�ł����B
�@�@ ���x�� x��v t (4-10)
(*1��)
�@v��t �ɑ��ĔC�ӂɕω�����ꍇ�C�������ԇ�tn�̊Ԃ�v�|t �O���t�����`�̖ʐς��ŗ^������B
0 ���� t (s)�Ԃ̕ψʂ� v�|t �O���t�̉��̖ʐ� �ŗ^������B
�@�ϕ����g����
�@�@(4-7),(4-8),(4-9)������ϕ����g���ċ��߂��
�@�@�����x�� dv �� adt �ϕ�����
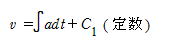
�@�@a ���Ct��0�� v��v0�Ƃ���� v��a t�{C1 �� C1��v0 �� v��v0�{at (4-7)
�@�@(4-7)������t�ɂ��Ĕ��������
�@�@���x�� dx��vdt �ϕ����ā@
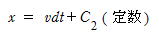
�@�@v��v0�{at ����
�@�@ t��0��x��x0�Ȃ�C2��x0 ��(4-8)
�@�@(4-8)������ t �ɂ��Ĕ����������v0�{at �� (4-7)
�� �}�͂��镨�̂�x����𐳂̌����ɓ����o���Ă���16�b��̑��x�Ǝ����̊W�������B
(1) �����x�Ǝ����̊W��}������B
(2) �ψʂƎ����̊W��}������B
��
(1)�E�}�P
(2)�E�}�Q
�@�@t��4�@�@x��(1/2)�~12�~4��24[m]
�@�@t��9�@�@x ��24�{(9�|4)�~12��84[m]
�@�@t ��12�@x ��84�{(1/2)�~(12�|9)�~12��102[m]
�@�@t ��14�@x ��102�|(1/2)�~(14�|12)�~8��94[m]
�@�@t ��16�@x ��94�|(1/2)�~(16�|14)�~8��86[m]
�@�@t ��0�`4�C14�`16[s]�͉��ɓʂ̕�����
�@�@t ��9�`14[s] �͏�ɓʂȕ�����
�@�@t ��4�`9[s] �͒���
�ړ������|���ԃO���t�͂ǂ��Ȃ邩���l���Ă݂�B
(���̓������x�Ԃ̕ψʂ̑傫���̘a���l����悢)
3 �x�N�g���ƃX�J���[
��5 �Ð����̑���v �̑D�ŁC������V (��v)�ŕ�l�̐���C����ɒ��p�ɉ�������ɗv���鎞��t �ƒn�ʂ��猩���D�̂� u�����߂�B�܂��D��i�߂�ׂ����������߂�B
��6 ���� v [m/s]�Ő}�̌����ɗ���Ă����̏��Ð��ɑ���c[m/s]�̑����Ői�ޑD�̉^���ɂ��ē�����B
(1) ��݂ɉ����đD�� l [m]�����������鎞��t�P[s]�����߂�B
(2) ��݂ɐ����� l [m]�����������鎞��t2[s]�����߂�B
(3) t1 �� t2 �Ƃłǂ��炪�傫�����B�������C�D�̌�����ς��邽�߂̎��Ԃ͖�������B
��7 �앝�� d [m]�ŁC������ v [m/s]�̈�l�ȗ���̐삪����B��݂̈�_�`���� l [m]�쉺�ɑΊ݂a�_�Ɍ������Ĉ꒼���ɑD��i�߂����B���̂Ƃ��C���ɑ���D�̑������ŏ��ɂ��邽�߂ɂ�
(1) �D�̌������ǂ̌����Ɍ����đ����悢���B
(2) ���̏ꍇ�C�D��Ð��ɑ��Ă�����̑����ő����悢���B
4-4 ���Α��x
��8 ��������80Km/h�̑����ő��鎩���Ԃ`���C����������100Km/h�̑����ő����Ă��鎩���Ԃa���猩���Ƃ��̑��x�����߂�B
��9 ���xu�Ő^���ɐi�ސl������B�����^�k�ɐ����Ă���悤�Ɋ����C���x��2�{�ɂ���ƕ��͖k�����琁���Ă���悤�Ɋ�����Ƃ����B���̐^�̑��x�����߂�B
��10 ��葬�x�̕��������Ă���Ƃ�����C�k�Ɍ�������5.0[m/s]�̑����Ői��ł���ƁC�����쐼���琁���Ă���悤�Ɋ����C�������k�Ɍ������đ�����20.0[m/s]�ɂ���ƕ��������琁���Ă���悤�Ɋ������B
(1) ���̑����͂����炩�B
(2) ���̑����̓�k����������v1�C��������������v2�Ƃ���v1�^v2�̑傫�������߂�B
4-5 �P�����̉^�� 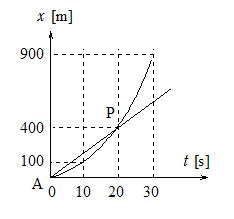
��11 �`�w�Ƃa�w�͈꒼���̃��[���ő����Ă��āC���[���ɕ��s�Ɏ����ԓ��H������B�����Ԃ��`�w��ʉ߂���Ɠ����ɓd�Ԃ��`�w���o���C��l�ɉ������āC�d�Ԃ�20[s]��Ɏ����Ԃ�ǂ��z�����B�E�}�͂`�w�����_�Ƃ��C�o�������Ƃ�������t ��0�Ƃ��Ď���t [s]�̂Ƃ��̓d�ԂƎ����Ԃ̂��ꂼ��̍��Wx[m]�������O���t�ł���B
(1) �����Ԃ͂ǂ�ȉ^�������Ă��邩�B
(2) �d�Ԃ̉^���̉����x�͂����炩�B
(3) �d�Ԃ������Ԃ�ǂ��z���Ƃ��́C�����Ԃ̐l�������d�Ԃ̑��Α��x�����߂�B
��12 x����𐳂̌����ɒ����^�����镨�̂�����B�͂��ߐÎ~���Ă������̕��̂��C����t��0[s]�ɉ����x�� [m/s2]�̓������x�^�����J�n�����B���̕��̂͑��xv [m/s]�ɒB������C���炭�̊Ԃ��̑��x�œ����x�^�� ���s��,���̌���̉����x�|�� [m/s2](����0)�Ō������Ď��� t��T [s]�ɂӂ����ѐÎ~�����B
(1) ���̊Ԃɕ��̂��ړ���������l [m]�����߂�B
(2) ����T �����ɂ��ċ���l ���ő�ɂ��邽�߂ɂ͑��xv���ǂ̂悤�ɂƂ�悢���B�܂����̂Ƃ��̋���l �Ɠ����x�^�����s���Ă��鎞�Ԃ����߂�B
��13 �������x�Œ����O���𑖂��Ԃ��C����n�_��ʉ߂����Ƃ��̗�Ԃ̑O�[�̑��x��v1,��[�̑��x��v2�ł������B
(1) ��Ԃ̒����̓_���ʉ߂����Ƃ��̑��x�����߂�B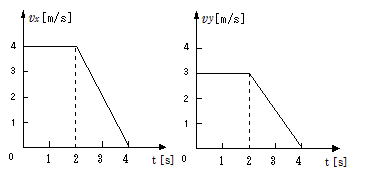
(2) ��Ԃ̑O�[����C�ӂ̋���x �̓_���ʉ߂����Ƃ��̑��x�����߂�B
��14 ������(xy��)����^�����Ă��鏬���̂�����B���� t ��0[s]�@�ɕ��͍̂��W�̌��_�n�ɂ���C���x v [m/s]��x����vx�C�����y ���� vy �Ǝ��� t [s]�Ƃ̊W�͐}�̂悤�ł������B
(1) ���� t��1[s]�̂Ƃ��̕��̂̑����͉�[m/s] ���B
(2) ���� t��3[s]�̂Ƃ��̕��̂̉����x��x �����͉�[m/s2] ���B
(3) ���͓̂����͂��߂Ă���4[s]�Ԃɉ�[m]�i���B
(4) x �� y �̊W�������O���t(���̂̉^���̋O�Ղ�\��)�̊T�v�������B
�z�[�� ���j���[ ���_������� �x�N�g���ƃX�J���[ ���̂̉^�� �� �^���̖@�� �~�^�� �d���ƃG�l���M�[ �^����
Top