ホーム  メニュー            序論･物理量   ベクトルとスカラー    落体の運動    力    運動の法則  円運動  仕事とエネルギー  運動量
                                                                             

【８】円運動
８−１ 等速円運動

一定の半径の円軌道を等速で運動すると，一定の速さで運動しているにもかかわらず加速度が生じている。なぜか。
等速円運動は速さは一定だが，速度は一定ではない。
点Oを中心に，半径 r で一定の速さ v の等速円運動を考える。点P，P' それぞれの速さはv だが，つねに向きを変えている。
角速度ω(角度の時間変化の割合)を()と定義する。単位は[rad/s]。
P点から円軌道を一周する時間を T (周期)とするとθ＝2πだから  ･･･････(8-1)
と書くことができる。
微小時間��tの円弧長を，PP' ＝��Sとすると，
          ∴        ･････････････････ (8-2)

等速円運動はω が一定。ω 一定でも r によってv が変わる
  同様にしてv の変化を考えると
P点の速さv がP'で速さv になるために，その変化��vの向きに加速度が生じる。
向心加速度aは  ･･･････(8-3)

円運動での加速度の例
等速円運動 向心加速度のみ	傾いたカーブ上の円運動 カーブの中心向きの向心加速度のみ カーブを進む場合，傾きがないと飛び出してしまうのは，なぜか
振り子の運動 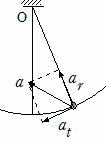円運動しているのだから，支点に向く向心加速度ar 不等速だから接線方向の加速度atも生じているので， 加速度の大きさは   である。	曲線運動 向心加速度ar＝は速度ベクトルの向きが時間に対して変化することが原因，接線方向の加速度は速さの変化によって生じたもの。加速度の大きさは 向心力 F＝ma＝mrω2 ＝m (これが円運動の原因である)

８−２万有引力

１７世紀初め，ケプラーは，ティコ･ブラーエの観測した惑星運動の記録を研究し，以下の法則を派遣し，ニュートンは万有引力の法則や運動の法則の発見の基礎を作った。
ケプラーの法則
 　 第１法則　惑星は太陽を一つの焦点とする楕円軌道を描く。
 　 第２法則　惑星と太陽を結ぶ動径は等時間に等面積を描く。
 　 第３法則　惑星の公転周期の２乗は太陽からの平均距離の３乗に比例する。
　　万有引力を導いたニュートンの考え方
　　仮定：惑星(質量m)は太陽(質量M )のまわりを半径rで速さvの等速円運動する。太陽は静止しているものとする。
　　惑星の円運動の運動方程式　m＝F  ･･･�@
　　ケプラー第３法則から，惑星の公転周期をT とするとk＝  ･･･�A (k は比例定数)
円運動の関係式から  2πr＝vT･･･�B
�@，�A，�B式から　  ･･･�C　(Kは比例定数)
このFは惑星が受ける力であるが，太陽も反作用としてF ' の力を受ける。F ' も�Cと同じ形の力を受けると考えるとF '＝K '，(K'は惑星を中心としたときの定数)  
　　| F |＝| F' | から K＝K '   ∴     (Gは万有引力定数)これと�@から  F＝G
　　万有引力定数G＝6.673×10⁻¹¹Nm²/Kgはキャベンディシュによって調べられている。

８−３ 人工衛星

静止している地球(質量M，半径Rの球とする)の周りを人工衛星(質量m)が地球の中止から半径r の円軌道を描いていると考える。地球の自転による影響を無視できるものとする。
重力加速度 g の高さ r との関係
　　　地表での重力加速度をg，高さr での値をg(r) とする。
　　　地表で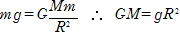      
 　　高さr で   　�@
　　　　　( g(r)∝1/r ²だから上空に行くほど重力加速度は小さくなる)
速さv と高さr の関係
　　　高さr で
               �A
　　　　　r＝R の場合g＝9.8m/s²，R＝6400Kmとすると
　　　　　v＝ (第一宇宙速度)
　　　　　(r が大きくなるとv が小さくなる→ケプラー第２法則)
周期Tと高さr の関係
　　　　　    2πr＝vTから　  �B
　　　　　(r が大きくなるとT が大きくなる→ケプラー第２法則)
　　　　　r＝R の場合g＝9.8m/s²，R＝6400Kmとすると
　　　　　

８−４ 慣性系と非慣性系

慣性系とは，ニュートンの法則が成り立つ座標系。実在の力だけで運動の法則が成り立つ系のこと。たとえば，
地上に静止している観測者から見た場合，物体が等速で運動しているとき物体と同じ速度から見た系。１つの慣性系に　対して等速度運動する座標系はすべて慣性系である。
非慣性系とは，加速度運動する座標系。この系では，実在の力だけでは運動の法則が成り立たない。
　「実在の力の他に，慣性力(質量mの物体に外力の和Fが働き加速度aが生じている場合，大きさはmaで
   実際の加速度と逆向き)を加えると物体はつり合いを保つ(これをダランベールの原理という)」，として運動を表す。
円運動での慣性力は遠心力である。

運動の調べかたの違い
  慣性系では，実在の力だけから，運動方程式を使って運動を調べる。
  非慣性系では，実在の力と慣性力を加えて，力の釣合い式を立てて運動を調べる。

ふつう地球表面上に固定して座標系を慣性系のように扱うが，地球の自転公転を無視した近似である。
慣性力は実在の力ではないので，慣性力の反作用の力はない。
固定軸のまわりに一定の角速度で回転している座標系から物体の運動を観察するとその物体が座標系に対して動いていれば，物体の速度と直角の方向に見かけの力(コリオリの力または転向力)が現れる。物体が座標系に対して動かなければ遠心力だけが現れる。コリオリの力は，北半球で台風が左巻きになる原因である。

円運動を調べるポイント
　  �@ 円運動の中心はどこか
　　�A 半径は
　　�B 向心力Fの原因は何か
　　　　(向心力という特別の力はない。それぞれの場合によって異なるが，必ず円運動の中心に向いている)
　　�C 運動方程式  mrω²＝F   または  m＝F

例1 右向きに一定加速度aで動く電車の中に天井から糸で釣られたの小球の運動を

慣性系では，地上に静止した人は，「小球が等加速度運動している」と見る。糸の張力と小球の重力の合力が，から水平方向でmgtanθ になるので，運動方程式を立て
 ma＝mg tanθ      ∴    a＝g tanθ   と等加速度運動であると決定する。





 非慣性系では電車の中にいる人は，小球が静止していると観測する。これは，慣性系でのとの合力と慣性力−maの和が 0 つまり，水平方向に力がつり合っていると考える。F＝mgtanθ だから，つり合い式を  
  　　  mg tanθ−ma＝0  
と書くことができる。慣性系と同一の数学的結果を得て，電車が大きさ a＝g tanθ の等加速度運動をしていると決定する。




例2 等速円運動する円板の中心に結ばれた長さr の糸につながれた質量mの小球について

慣性系では，地上に静止した人は 「小球は円板とともに等速円運動する」 と見る。糸が小球を引く力(張力T )が向心力となっているためである。
運動方程式は   m＝T  


非慣性系では，円板上にいる非慣性系の人は「自分も小球も円板に対して静止している」と見る。これは，糸の長さ方向の力がつり合っているためで，糸の張力と慣性力としての遠心力の和が 0 であるためである。
つり合い式は  T− m＝0  と　なり，慣性系と同一の数学的結果を得る。




例3 長さl の糸の上端を固定し，下端に質量mのおもりをつるし，これを水平面内で等速円運動させる(これを円すい振り子という)。糸が鉛直線となす角度をθ とするときの糸の張力T，円運動の角速度ω，おもりの速さv，円運動の周期T を求めよ。ただし，重力加速度の大きさをg とする。

解 慣性系で考える。糸の張力をSとすると，円運動の原因となる向心力はSと重力mgの合力でその大きさは，mgtanθである。
おもりに働く鉛直方向の力の釣合いから，Scosθ＝mg           ∴    
円運動の半径r は r＝l sinθ だから，円運動の運動方程式は
     mrω²＝m(rsinθ )ω²＝mg tanθ   ∴ ω＝
おもりの速さv は  v＝rω＝l sinθ ＝
周期T は(8−1)式から   ＝2π
非慣性系で考えた場合は
     鉛直方向で Scosθ ＝mg
    水平方向で Ssinθ ＝m(l sinθ )ω²  (遠心力)
のつり合い式から，が求められる。以下は慣性系と同じ。

【９】単振動

質点が復元力，つまりx軸上の定点Oからの距離に比例する引力−Kx ( K＞０)を受けてx軸上で行う往復運動を単振動をいう。Kは単振動する系によって決まる固有の値である。復元力の例としては，ばね振り子の場合は弾性力，単振り子の場合は重力の分力，浮き子(液体中に浮かせたもの)の場合は浮力などである。
単振動する物体の運動方程式は
　　　　 ma＝−Kx        (9-1)
であり，変位 x はx＝Asin(ωt＋φ )
速度vは  v＝＝Aωcos(ωt＋φ )
加速度aは  a＝＝−sin(ωt＋φ )＝−
ここに，Aは振幅，ωは角振動数，(ωt＋φ )は位相，φ は初期位相であり，a，φ は初期条件できまる。
周期T (同じ状態にもどる時間)は   　　(9-2)    である。
Kx の意味
　　　　x＞0 のとき −Kx＜ 0
　　　　x＜0のとき −Kx＞ 0
　　　　つまり，常に振動中心に向かう向きに復元力がはたらくことを示している。
　　　　単振動の特徴を示す量は，周期T ，振動中心，振幅などである。

単振動を調べるポイント
　　�@ 物体の運動方程式を立て，合力が−Kxの形であるか調べる。
　　�A 物体の加速度aを求め，a＝−ω²x から角速度ωを求める。
　　�B 周期T はから求める。
　　�C 振動中心は加速度a＝0 の位置である。
　　�D 振幅は，初期位置から振動中心までの距離

例1 ばね振り子  
ばね定数kのばねの上端を天井に固定し，下端に質量mの小球を取りつける。つり合い位置からから下にx₁引き延ばし瞬間的に放した。摩擦がないものとしてどのような運動をするか調べよ。

解 下向きを正の向きにし，つり合い位置からの伸びをx とする。つり合い位置での自然長からののびをx₀とするとは，つり合い式は mg＝kx₀
任意の時刻の運動方程式は，加速度をa とすると
　　    ma＝mg−k(x₀＋x)＝−kx ← 単振動である
書き換えると  a＝＝−     ∴  ω＝
周期Tは＝        (9-3)
振動中心はa＝0だから，x＝0 つまり，つり合い位置である。振幅はx₁である。
(水平と角度θ をなした斜面上で同様に単振動させた場合も周期は変わらない。つり合い位置が x₀＝である。
θ ＝90ﾟが鉛直ばね，θ＝0 が水平ばねである)

例2単振り子
軽い糸(長さl )の一端を固定し，下端に小さなおもり(質量m)をつけ，固定点を含む鉛直面内で左右に振動させる。糸が鉛直線と角θ (rad)をなす瞬間について考える。重力加速度の大きさをg とする。

解 おもりに働く力は重力mg，と糸が引く力S である。
運動方程式は，加速度をa とすると
         ma＝− mg sinθ＝−mg≒−mgθ が小さい場合，円弧≒変位xであり，sinθ ≒θ ≒x／l
加速度aは a＝＝−     ∴  ω＝
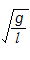
周期T は  ＝2π        (9-4)
（8-4慣性系と非慣性系 例題3 円すい振り子の周期の式でθ ＝0 にした場合と同じ結果である） 

単振り子の周期は重力加速度が関係しているので，どのような運動系で単振動しているかによって周期が異なる。
等加速度aで上昇する運動系では，等加速度aで下降する運動系では
水平方向に等加速度aで運動する系では
水平と角度θをなす斜面上では
である。

θ≒0でない場合，周期T は角度の関数として次式で与えられる。
       
この式の積分は第１種の完全楕円関数と呼ばれるものである。積分を近似すると
       
と表すことができ，さらにθが小さい場合
      なので
     
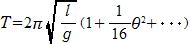
で与えられる。

θ の最大値が10ﾟで約0.19%，7ﾟで約0.09％ の誤差を生じる。周期T はおもりの質量，振幅に関係しない

例3 水に浮くストロー
長さl の質量を無視できるストローの下端に質量mの粘度の小さな塊Pをはめ込み，密度ρの液体に立たせる。上端を少し下方に押して支えを急に取り去ると上下運動する。この運動を調べる。

解
ストローの断面積をS，つり合い状態で液体中のストローの長さをl₁とすると，Pについてのつり合い式は，重力＝浮力から
　　　　　mg＝l₁Sg×ρ     ∴   m＝l₁Sρ   ()
つり合いの状態からx沈んだ状態でのPの運動方程式は，加速度aとすると
    　　　ma＝mg−S (l₁＋x )ρg＝−(Sρg) x＝
加速度aは  
周期T は  ＝2π       (9-5)
これは単振り子と同じ形である。また，(8-3)人工衛星最終行の地表すれすれを運行する人工衛星の周期もであり，これも同じ形である。

                                                         演習問題                           解答

以下の問で必要なら重力加速度の大きさをg とせよ。
8-1 等速円運動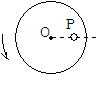
問51 mg[N]の重さまで吊すことのできる長さr の紐におもりをつけて，なめらかな水平台の上で回転させる。糸が切れる直前のおもりの速さはいくらか。
問52 半径r で傾斜のないカーヴを質量M の車が速さv で走る。タイヤがスリップしないためには，道路とタイヤ間の摩擦係数μは少なくともいくらでなければならないか。
問53 鉛直な軸Oまわりに回転できる円板上で，Oからの距離 r の点Pに小物体を置く。
       円板を回転させてその角速度をゆっくり増加させて，ω₀を越えると，小物体は円板上をすべった。すべり出す直前の状態で，小物体に働いている摩擦力の向きと静止摩擦係数μ をω₀，r，g で表せ。

8-3 人工衛星
問54 極に比べ赤道上の重力加速度はどれだけ小さいか。
問55 地表から地球の半径と同じ高さでの重力加速度はいくらか。ただし，地表での重力加速度g＝9.8[m/s²]とする。
問56 静止衛星(周期が地球の自転周期と同じ)の高さを求めよ。
問57 地球のまわりを質量m の人工衛星がまわっている。地球の質量はM，万有引力定数はGである。はじめ人工衛星の軌道は，地球の中心からの距離の最大値がr₁，最小値がr₂のだ円であった。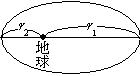
(1) この人工衛星の速さが最小になったときの速さをv₁とすると，地球の中心からの距離がr₂のときの速さはいくらか。
人工衛星が地球の中心から最も遠い位置に来たとき，燃料を噴射して，半径r₁の円軌道に移るものとする。
(2) 半径r₁の円軌道をまわるためには，人工衛星の速さはいくらであればよいか。
(3) はじめのだ円軌道の場合の周期T，円軌道になってからの周期をT₁とするとき， をr₁，r₂で表せ。

8-4 慣性系と非慣性系
問58

遊園地の乗り物ローターでは，回転数がある速さ以上になったときに床を下げると，人は壁に押しつけられてまま回転する。人と壁との間の静止摩擦係数をμ，ローターの半径をr とすると，人が床に落下しないための最小回転数を求めよ。

問59

バケツに水を入れ，鉛直面内で水がこぼれないように振りまわすには，最高点での速さをいくらにすればいいか。回転半径をr とする。

問60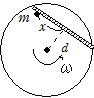

図は,中心から距離d の位置に角材を打ちつけた円板を上から見たものである。この角材の中心からx の距離に質量m の小さな物体を置き，円盤を水平面内の矢印の方向に,一定の角速度ωで回転させる。物体は角材によって遮られており,角材の反対側には出ないものとする。円板の表面と物体との接触はなめらかであり,物体と角材との間には静止摩擦係数μの摩擦があるものとする。
(1) 物体が円板上をすべらずに,円板とともに等速円運動しているとき,物体に働く角材からの垂直抗力N および摩擦力Fが働く。観測者が円板の上に立つと物体が静止しているように見える。この観測者から見て,この物体にはどのような力が作用していると考えられるか。相対的な大きさに注意して,考えらえる水平方向の力のベクトルをすべて図に書き込め。
(2) この物体がすべらずに等速円運動するとき，N，F の大きさを求めよ。ただし,円板は十分大きいものとする。

問61

水平な道路のカーヴを半径r の円弧状にして電車が一定の速さvで安定して走れるようにしたい。そのために,路面を内側に傾斜させ(この高さの差をカント＝cantという)，路面上で電車の横すべりをもたらす力が０になるようにしなければならない。このとき，路面の最適な傾き角をθ とするとき，速さv とθ の関係式を求めよ。

問62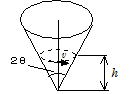

頂角２θ の円すいを，頂点を下にして，軸を鉛直にして立てる。小物体がこの円すいをなめらかな内面に沿って，頂点からの高さh の水平面上を等速円運動するためには，その速さをいくらにしたらよいか。

9 単振動
問63

図に示すように，水平面上を滑らかに動く台がある。この台の上には水平に置かれた，質量が無視できるばねがあって，その左端は台に固定してあり，右
端には質量m の物体Ｐが取り付けられている。この物体Ｐには，それと等しい質量mの物体Ｑが接合されている。台が静止している状態でばねは自然の長さになっている。このときのPの位置を原点（x＝0）として，ばねと平行に台上に固定したx軸を取り，右向きを正とする。ただし，P，Qの大きさは無視する。P，Qと台との間には摩擦はない。ばね定数はk とする。P，Qが接合して一体となった状態で台をばねと平行に右向きに一定の加速度a で動かし始める。すると，P，Qは台上から見て単振動をする。この単振動の中心のx座標，振幅を求めよ。また台を動かしはじめて，Pが最初にx＝0 に戻って来るまでの時間を求めよ。

問64

図のように,電車が水平な直線のレール上を一定の加速度α で走っている。長さl の糸に,質量mのおもりをつけて電車の天井の点Ｏからつるした。時刻 t＝0で,糸がたるまないように,天井に対して垂直な位置から静かに離したとき,車内に静止した観測者から見たおもりの振動について，α ≪g とし空気抵抗は無視できる場合について，おもりの振動の中心が,天井に対して垂直な線となす角度θ₀とこの振動の周期を求めよ。

問65  図に示すＡは１[m]伸ばすのにk[N]の力を必要とするつるまきばねである。その上端を固定して鉛直につるしてある。ばねの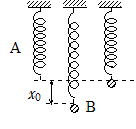質量を無視する。

(1) ばねの下端にm[Kg]の物体Ｂをつり下げたとき,ばねはx₀[m]伸びてつり合った。x₀はいくらか。
(2) つり下げた物体Bを図のx＝0（xは伸縮量）の位置まで持ち上げてから，静かに離す。x の時間変化をグラフに書け。
ただし，Tは物体の振動周期で，x はばねが伸びた場合を正とする。
(3) (2)の場合に物体Ｂに働く力f はどのように変化するか。グラフで示せ。ただし，f はばねの伸びる場合を正とする。

問66 フックの法則に従う理想的なバネがあり,その自然長はl,バネ定数はkである。このバネに質量mの小球をつけて,図のように内面のな

めらかな細い円管の中に入れ,バネの一端をＡ点に固定する。そして小球の真下の点Ｏ,すなわちＡから距離l の点Ｏを通る鉛直線を回転軸として円管を水平面内で一定の角速度ωで回転させる。そして小球をＯから少しづつずらしてやると,小球は円管内でＯ点を中心として微小振動をはじめた。
(1) 小球がO点からxずれたとき,小球に働く遠心力とバネの復元力の大きさを求めよ。
(2) 小球に働く力の合力を求めよ。ここで,力は円管の軸方向の成分だけを考え,バネの伸びる向きを正とせよ。
(3) 小球が微小振動を行うための条件を求めよ。
(4) この微小振動の角振動数を求めよ。また,円管が一回転する間に,何回の微小振動が行われるか。

問67

図のように，半径がr の円筒A，Bを接触させて水平に並べ，この上に質量mの一様な棒を円筒の軸方向に直角に置いて，円筒を同時に等しい速さで図の矢印の向きに回転させる。円筒と棒との間の動摩擦係数をμとする。棒はどのような運動をするか。

解答

ホーム  メニュー            序論･物理量  ベクトルとスカラー   落体の運動    力    運動の法則  円運動  仕事とエネルギー  運動量
           Top