ホーム メニュー ![]() 序論・物理量 ベクトルとスカラー 落体の運動 力 運動の法則 円運動 仕事とエネルギー 運動量
序論・物理量 ベクトルとスカラー 落体の運動 力 運動の法則 円運動 仕事とエネルギー 運動量
【10】仕事とエネルギー
10-1 仕事
仕事とは、「一定の力Fが作用して変位 s が生じるとき,その変位方向の力の成分とその変位の大きさとの積」と定義される。
仕事Wは W=F s cosθ ・・・ (10-1)
である。( θ はF とs のなす角度)
単位は N・m=J (ジュール)または,dyne・cm=erg(エルグ)
F とs のスカラー積を使って表すと,
W=F・s と表すことができる。
(仕事は,力ベクトルと変位ベクトルとの内積で与えられ,スカラーである。つまり仕事は向きを持たない量である)
仕事の正負(物体の運動方向が右の場合)
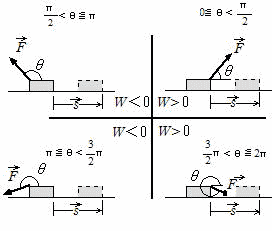
変化する力のする仕事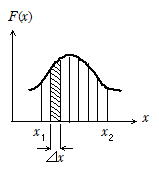
物体に加える力が一定でない場合
⊿x の区間での仕事は ⊿W=F(x)⊿x
x=x1からx2の全区間での仕事Wは
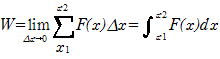
仕事はF(x)-x グラフの面積で与えられる
仕事率P
仕事は時間に関係しないが,仕事の時間に対する変化の割合を仕事率という。
仕事率Pは,仕事をW,仕事をした時間をt とすると![]() で定義される。
で定義される。
また,一定の力を加え,速さvとすると
![]() ・・・ (10-2) で与えられる。
・・・ (10-2) で与えられる。
仕事率の単位は[P]=J/s=W(ワット)である。
1N=1Kg・m/s2、1dyne=1g・cm/s2
仕事の正負は,変位の向きと加えた力の変位方向成分が同じ場合に正,逆向きの場合負である。
右向きに力を加えて右向きに動いても,左向きに力を加えて左向きに動いても仕事は正である。つまり,右向き,左向きの仕事という言い方は誤りである。
道具を用いて力や距離を変えられても仕事量を変えることはできない。これを仕事の原理という。
Wは人名J.Watt(1736~1819)の頭文字。人名に由来する単位名は大文字にする
10-2 力学的エネルギー保存(law of mechanical energy conservation)
保存力(conservative force)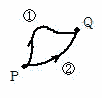
一般に2点間を運動する質点に作用する力が仕事をするとき,その仕事が経路に依存しない力(例 重力,弾性力,電磁気力)。保存力が働く場合(そのような場を保存力場という)点PからQに移動させるとき,経路①を移動させても,経路②を移動させても,仕事が同じである。
ポテンシャルエネルギー(位置エネルギー)
ポテンシャルエネルギー(位置エネルギー)は,
「基準点(P点)からQ点までゆっくり移動させるのに要する外力のする仕事=Q点から基準点(P点)まで移動させる保存力のする仕事」
と定義する。位置エネルギーはスカラーである。
重力による位置エネルギー(g 一定とした場合)
地面から高さhの位置にある質量mの質点の地面に対する位置エネルギーUは,重力加速度g を一定とすると
U=mgh である。 (10-3)
(基準点(地面)から高さhまで質点をゆっくり鉛直上方に移動させ,外力(mg)を鉛直上向きに加えるから変位hの向きと外力mg の向きが同じ向きなので U=mg×h=mgh となる)
万有引力場での位置エネルギー
基準点を無限遠にとり,基準点の位置エネルギーを0とする。
「地球から距離r の位置から基準点まで質量m の物体を移動させるのに要する万有引力のなす仕事」
または
「基準点から,地球から距離r の位置まで質量m の物体をゆっくり移動させるのに必要な外力のなす仕事」
と定義される。外力の場合の「ゆっくり移動」は2点間の位置の違いだけ考えるので,運動エネルギー=0とするためである。位置エネルギーUは
(10-4)
弾性力による位置エネルギー
ばねなどの弾性力はFS=-kx (kはばね定数,xは自然長からの伸縮量)である。
FS=FとなるFを外力とするとき,ばねを⊿x伸ばす(縮める)ために外力Fがした仕事⊿Wは⊿W=F⊿x
外力Fがx=0→ x=xmまでばねをゆっくり伸ばす(縮める)仕事Wは
よって,自然長からx 伸ばされた(縮められた)ばねの弾性エネルギーUは
(10-5)
位置エネルギーの基準点は任意で差だけが問題。ゆっくり移動させるのは,位置の違いだけ考えるため。
P点からQ点まで移動させるための位置 x での保存力保存力 F (x) のする仕事Wは,P点,Q点での位置エネルギーをそれぞれ UP,UQとすると
∴
つまり,保存力 F (x) の大きさは位置エネルギーの位置に対する傾きで,向きは位置エネルギーが減少する向きである。

地球内部の万有引力,位置エネルギー (クリックで詳細表示)
運動エネルギー(kinetic energy)
速度v,質量mの質点に一定の力-F(N)を加えて止める(v=0)。この間s(m)移動するときに外力が質点にした仕事は,運動方程式から
ma=F ∴(一定)
等加速度運動の式から
質点は静止するまでにの仕事をすることができる。このように運動する物体が持っているエネルギーを運動エネルギーという。
運動エネルギーKは(10-6) である。運動エネルギーもスカラーである。
仕事-エネルギーの定理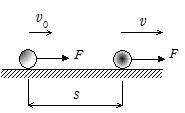
図のように速度v0で運動する質量mの質点が,速度と同じ向きに一定の力Fを受けて,距離s進んだときの速度がvになった場合,加速度a=F/m(一定)だから,
等加速度運動の式から
・・・ (10-7)
これを,仕事-エネルギーの定理という。
質点の運動エネルギーの変化量は質点に作用する力のする仕事に等しい
質量mの質点を位置x1からx2に一定の力Fを加えて移動させたときの仕事W は,加速度aが
だから
力学的エネルギー保存
位置エネルギーUと運動エネルギーKの和を力学的エネルギーEと呼び,保存力だけが働く系では力学的エネルギーは保存される。
E=U+K=一定
重力だけがはたらく場合は E=mgh+=一定
重力,ばねによる弾性力がはたらく場合=一定・・・ (10-8)
非保存力が働く場合の仕事-エネルギーの定理
現実の運動では摩擦抵抗などの非保存力が働くので,力学的エネルギー保存の法則は成り立たない。つまり、その仕事が経路に依存する。しかし,仕事-エネルギーの定理を使って次のように考える。
非保存力が系になす仕事を⊿E(<0),はじめの状態,後の状態の力学的エネルギーをそれぞれE1,E2とすると,
E2-E1=⊿E または E1+⊿E=E2 ・・・ (10-9)
つまり、非保存力がする仕事は系の全力学的エネルギーの変化に等しい。
単振動のエネルギー
エネルギーの例の一つとして単振動のエネルギーを考えてみる。
質量mのおもりにバネ定数kのバネを取りつけた水平バネを考える。振幅をA,振動数をf とすると,エネルギーEは
E=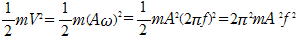
つまり,単振動のエネルギーは振幅A,振動数f の2乗に比例することが分かる。
例1 質量mの小球を地上h の高さから自由落下させた。地上y(<h)での速さを求めよ。ただし,空気抵抗は無視する。
解 地面を高さの基準とする。地上hでの位置エネルギーはmgh,地上yでの位置エネルギーはmgyでここでの速さをv とすると運動エネルギーは
である。地上h,yでの力学的エネルギー保存から
mgh=mgy+∴
なめらかな斜面上の地上hの高さの位置から初速度0で落下させた場合も同じ結果になる。
例2 質量mの小球を地上hの高さから上方に初速度v0で投げ上げた。地上yの高さでの速さvを求めよ。空気抵抗は無視する。
解 前問と同様にして,地上h,yでの力学的エネルギー保存から
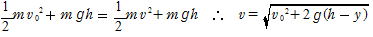
この結果のvは,投げ出す向きがどのようであっても(上方,投げ下ろし,水平投射,斜方投射)に関わらず同じであることに注目したい。なぜなら,エネルギーがスカラーだからである。
例3 長さ l の軽い糸に質量mの小球をつけた振り子がある。空気抵抗は無視できるものとする。はじめ鉛直線となす角度θ0で糸がたるまない状態(P点)にして静かに放す。角度がθ (Q点)になったときの小球の速さvとこのときの糸の張力Tを求めよ。
また,小球が図の左側に達した後,再び右側に角度θ' に達した瞬間に糸を切った。その後のおもりの最高点の高さを,糸が切れる前のこの運動の最下点からの高さHを求めよ。
解 振り子の最下点を高さの基準として,P,Q点間で力学的エネルギー保存の法則から
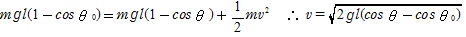
(糸の張力は振り子の運動方向と常に直交しているので仕事をしない)
糸の長さ方向の運動方程式を立てると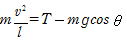
(は向心加速度。右辺が向心力で,振り子の支点に向いている)
vを上記の2式から消去して
(θ0=90°,θ=0での場合で,これは例1で(h-y)=l とすると同じ結果)。
θ=θ ' とすると ,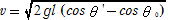
糸を切断した位置と最高点(速さは)で
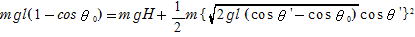
例4 粗い水平面上で質量m の物体に初速度v0を与えたところ、距離lだけ移動して止まった。物体が動き始めてから、距離x(<l) 移動したときの速さvを求めよ。
解 床面の摩擦力Fが物体にした仕事を⊿Eとし,v=v0とv0=0 の位置間で力学的エネルギー保存の法則を適用して
はじめの位置を距離xでの力学的エネルギー保存の法則から
( x=0でv=v0,x=l で v=0)
例5 ばね定数k のばねの一端を壁に固定し、他端に質量mの小球を取りつけ水平でなめらかな面上に置いた。自然長からx0だけ引き伸ばして静かに放した。小球が自然長から伸縮量がx での速さvを求めよ。摩擦は無視できるものとする。
解 はじめの位置と,伸縮量がx の位置で力学的エネルギー保存の法則を適用して
( x=x0でv=0,x=0で v=)
演習問題 解答
以下の問いで必要なら重力加速度の大きさをgとせよ。
10-1 仕事とエネルギー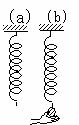
問68 ばね定数kの軽いばねを図(a)のように天井からつるした。図(b)のように自然長の状態のばねの下端に質量mの小球を吊し,手で支えてゆっくり下降させていった。
(1) ばねの伸びがx の状態のとき,手に加わる力はいくらか。
(2) 手が支える力が0になるときのばねの伸びはいくらか。
x が0から(2)の状態になるまでの間に
(3) 重力が小球になした仕事はいくらか。
(4) 手が小球になした仕事はいくらか。
(5) ばねをふたたび図(b)の状態にもどし,小球の支えを急にとった。ばねの伸びがxのときの小球の速さを求めよ。
(6) ばねが最も下がったときのx の値は(2)と異なる。その理由を記号を使って述べよ。
![]() 問69 質量m のおもりに軽くて細い糸をつけ,図のように棒のおもりに近い部分を手でつかんで静止させる。手の位置は変えずに力を少し緩め,摩擦力を一定に保ちながらおもりに等加速度運動させたところ,はじめのt [s]間にl [m]落下した。
問69 質量m のおもりに軽くて細い糸をつけ,図のように棒のおもりに近い部分を手でつかんで静止させる。手の位置は変えずに力を少し緩め,摩擦力を一定に保ちながらおもりに等加速度運動させたところ,はじめのt [s]間にl [m]落下した。
(1) おもりの加速度はいくらか。
(2) l [m]落下したときの速さはいくらか。
(3) おもりが距離l [m]落下する間に重力がした仕事はいくらか。
(4) おもりがl [m]落下しはじめたt [s]間に,手と棒の間で発生した熱量は位置エネルギーと運動エネルギーの差で与えられる。発生した熱量は位置エネルギーの変化量の何倍になるか。
10-2 力学的エネルギー保存の法則
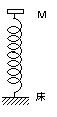 問70 ばね定数kのばねを鉛直に立て,下端を水平な床に固定し,上端にきわめて軽い皿を取りつける。皿の上に質量mの小物体を静かに置いた。
問70 ばね定数kのばねを鉛直に立て,下端を水平な床に固定し,上端にきわめて軽い皿を取りつける。皿の上に質量mの小物体を静かに置いた。
(1) ばねの縮み量はいくらか。
(2) ばねに蓄えられている位置エネルギーはいくらか。
つぎに,皿から高さh の位置で小物体を静かに落下させた。
(3) 小物体が皿に達したときの小物体の速度はいくらか。
(4) 小物体の落下によるばねの縮み量の最大値はいくらか。
問71 軽いつるまきばねの一端を床に固定し,他端に質量M [Kg]の板をつけて,その上に質量m[Kg]の小球を載せたら,ばねが自然の長さからd [m]縮んだ位置でつり合った(図a)。ばねは鉛直方向のみ伸び縮みするものとする。また,位置の問については,つり合いのときの小球の位置を原点,鉛直上向きをyの正の向きとして座標で答えよ。いま,ばねをつり合い位置から2d [m]だけ押し縮めて放す(図b)。
(1) 小球の座標が y [m]のとき,板が小球を押す力は何[N]か。
(2) 小球が板から離れる位置はどこか。
(3) 小球が板から離れるときの速さは何[m/s]か。
問72 図において,曲線ARSTBは紙面に垂直な方向に水平に伸びるなめらかな面を鉛直な平面で切った断面である。点PとQは点Sを通る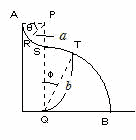 鉛直上にあり,2直線APとQBは水平である。曲線ARSは点Pを中心とする半径aの円の一部で、曲線STBは点Qを中心とする半径bの円の一部である。点Aで質量mの小物体を静かに放した場合の運動を考える。運動に対する空気抵抗は無視する。
鉛直上にあり,2直線APとQBは水平である。曲線ARSは点Pを中心とする半径aの円の一部で、曲線STBは点Qを中心とする半径bの円の一部である。点Aで質量mの小物体を静かに放した場合の運動を考える。運動に対する空気抵抗は無視する。
(1) 物体が点R(∠APR=θ )を通過するときの速さvR,,面から受ける垂直抗力NRを求めよ。
(2) また![]() がある値より小さい場合は点Sを通過した後も,しばらく面上をすべる。そしてある点T(∠SQT=φ )に達したときの速さをv とすると,点T で物体が面から受ける垂直抗力NTを求めよ。
がある値より小さい場合は点Sを通過した後も,しばらく面上をすべる。そしてある点T(∠SQT=φ )に達したときの速さをv とすると,点T で物体が面から受ける垂直抗力NTを求めよ。
(3) 小物体が点Sを通過した直後に面から離れて空中に飛び出すためのの条件を求めよ。
問73 一端Oを固定した長さlの糸に,質量mのおもりをつけて,図のように水平面上にあるA点から静かに離す。お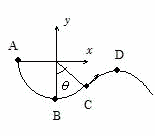 もりが最下点Bをすぎて角度θ (<
もりが最下点Bをすぎて角度θ (<![]() )だけ上がったところで糸を静かに切ったところ,おもりは最高点Dまで上がり,その後落下した。ただし,糸の質量,おもりの大きさおよび空気抵抗は無視する。また,座標はO点を原点とし,水平方向(右向きを正)をx 軸,鉛直方向(上向きを正)をy軸とせよ。
)だけ上がったところで糸を静かに切ったところ,おもりは最高点Dまで上がり,その後落下した。ただし,糸の質量,おもりの大きさおよび空気抵抗は無視する。また,座標はO点を原点とし,水平方向(右向きを正)をx 軸,鉛直方向(上向きを正)をy軸とせよ。
(1) 糸を切った点Cにおけるおもりの速度をx成分,y成分に分けて求めよ。
(2) D点のx 座標,y 座標を求めよ。
(3) D点のx 座標が最大になるためには,θ をいくらにすればよいか。
問74 図のような傾斜軌道ABを下り,半径a のなめらかな円形軌道の内側を質点が運動する。出発点Aの高さをh として,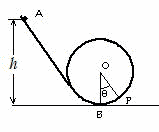 A点から初速度0で落下させた。質点の質量をmとし,空気抵抗は無視できるものとする。
A点から初速度0で落下させた。質点の質量をmとし,空気抵抗は無視できるものとする。
円形軌道の最下点Bと角度θ をなす位置P点での速さをv,面から質点が受ける抗力をN とする。
(1) P点での運動方程式を書け。
(2) A点とP点間での力学的エネルギー保存の法則を書け。
(3) P点で質点が面から抗力N をh,θ,a を使って表せ。
(4) 質点が角度θ が 0<θ <90゚の範囲で止まる場合,このときのcosθ をh,a をNを用いないで表せ。
(5) 質点が円軌道をまわるのに必要な最低の出発点の高さh0はaの何倍か。
ホーム メニュー 序論・物理量 ベクトルとスカラー 落体の運動 力 運動の法則 円運動 仕事とエネルギー 運動量
Top