序論･物理量 ベクトルとスカラー 落体の運動 力 運動の法則 円運動 仕事とエネルギー 運動量 ホーム メニュー 序論･物理量 ベクトルとスカラー 落体の運動 力 運動の法則 円運動 仕事とエネルギー 運動量
【７】運動の法則
ニュートンの運動の法則は以下の３つからなる。（下注参照）
第一法則(慣性の法則)
物体に外部から力が働かないか、働いていても合力が０のときは、物体は静止の状態を含めて、その運動状態を続けようとする。
物体の持つこの性質を慣性という ( これはガリレオによって発見された)。
第二法則(運動の法則)
質量mの物体に生じる加速度a は、物体に作用する合力 F の向きに生じ、その大きさは力 F の大きさに比例し、質量 m に反比例する。
比例定数を k とすると
で表される。これを運動の法則という。
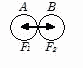第三法則(作用反作用(action and reaction)の法則)
物体Ａが物体Ｂに力FBをおよぼせば、同時に物体Ｂも物体Ａに力FAをおよぼしている。
２力FAとFBは大きさが等しく、作用線が一致するが、互いに反対向きである。
式ではFA＝－FBである。これを作用反作用の法則という。
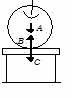例 机の上にリンゴが置いてある。これらには，図のようにA，B，Cの力が働いている。作用反作用の関係の力はどれか。
解 作用反作用の関係にある力は，AとBを入れ替えた関係にあり，別の物体に働いている。つり合いの力は同一物体に働きその和が０になる関係の力である。Aはリンゴの重力，Bは机→リンゴ，Ｃはリンゴ→机作用反作用の力はB，C，つり合いの力はA，Bである。
（注） これらは、３巻からなる著書『プリンキピア』の第１巻に記されている。ハレーに勧められて最初に公表したのは1685年、ニュートン44歳の時。『プリンキピア』には運動の法則のほかに微積分についてふれられている。つまり、距離を時間で微分すれば速度、速度を時間で微分すれば加速度になる。逆に、加速度を時間で積分すれば速度、速度を時間で積分すれば加速度になる、という方法を提示した。『プリンキピア』は "Mathematical Principle of Natural Philosophy" で和訳は『自然哲学の数学的原理』である。
ニュートンは、タルターリアに始まり、後にステヴィン、ガリレオ，ホイヘンスによって展開された力学上の数々の成果や、コペルニクス、ブラーエ、ケプラー、ガリレオ、ホイヘンスによる天文学上の諸々の業績を系統立てて、ひとつにまとめた。最初の二法則は彼の先駆者たちの研究によってすでに定義されていたが、それらを厳密に数式で表わし、論理的に系統立てたのはニュートンが最初であった。第三法則がニュートンの力学上の業績でとりわけ独創的なものである。
ニュートンの最大の業績である万有引力論が登場するのは第三巻。その中でニュートンは、二つの物体はある力をもって相互に引き合うこと、そして、その力はその物体の質量に正比例し、物体の間の距離の二乗に反比例するという相互引力の法則がすべての物体にあてはまると主張している。ケプラーの第三法則、およびホイヘンスが1673年その主著「振子時計」に書いている等速円運動の場合の求心力を求める公式から導かれる結論、力は二つの物体間の距離に反比例しなければならないということはニュートンはもちろん、ロバート・フックならびに他の科学者たちを当時すでに知っていた。しかしこの法則は、等速円運動をしている物体や天体などにのみ応用できるので、ケプラーの第一および第二法則に従うような楕円運動をするものには適用できなかった。ニュートンはそれら全てを総合し、引力理論に基づいて、力学を宇宙全体の学問に用いられることを確かにした唯一の科学者だった。すなわちニュートンは、極微粒子から巨大な天体に至るまで宇宙にあるすべてのものにあてはまる単純明快な理論を樹立した。これこそがニュートンの万有引力理論である。
７-１ 質量(mass)と重さ(weight)
① 地球が質量mの物体を引く力が重力であり，重力の大きさが重さWである。 重力加速度の大きさを gとすると
W＝mg (7-1)
重力単位系での力の単位はkgwであり １kgw＝1×9.8＝9.8N
② 質量
慣性質量･･･ 運動方程式から，力と加速度の割合つま り物体の慣性を示す。
(静止していれば静止し続けよう，ある速さで動いていればその運動状態を保とうとする性質の慣性を質量
で表す)
重量質量･･･ W＝mg から，つまり重さW と g の割合である。
の２種類あるが，その大きさが等しいことは証明されている。
重さ1キロの物体の場合 質量m＝1[Kg]，重さW＝mg＝1[Kgw]＝1×9.8＝9.8N
１円玉102個の 質量は0.102[Kg] 重さは0.102×9.8＝1[N]
重さと質量は異なる量であることに注意
７-２ 運動方程式(equation of motion)
第二法則は以下のようにして検証することができる。
水平な床の上に質量mの台車を置き、水平方向に一定の力Fを加える。加速度をa として，a とF，a とm の関係を調べる。
① 質量m一定で力Fを変化させ，それぞれの場合の加速度a とF の関係を調べる。
② 力F を一定にして質量m を変化させ，それぞれの場合の加速度a とm の関係を調べる。
①，②のまとめ
質量m，加速度a，物体に働く力の和をF とすると
m 一定の場合，a ∝F， F 一定の場合，a ∝(１／m)
これらの実験結果から(kは比例定数)運動の第２法則が得られる。
力の単位
ここでk＝１とするため，単位系を揃えて(ＳＩ単位系)での単位は
加速度 a[m/s2]，質量m[Kg]，F [Kg･m/s2＝N(ﾆｭｰﾄﾝ)]とする。
k＝１として(7-2)
これを運動方程式という。
数値計算を行う場合，力の単位は必ずＮ(ﾆｭｰﾄﾝ)とする。
位置座標をrとして微分を使って表すと
運動方程式のたてかたのポイント
手順 ① 対象物体に働く重力と接している物体からの接触力を書き出す。
手順 ② 調べる方向の力の正の向きをきめ，力の各成分を書きだし，合力を求める。
手順 ③ 調べる運動方向について②の合力から運動方程式をたてる。
例題1 質量がそれぞれ M， mの小物体A，Bがある。図のように物体Ａは水平でなめらかなで床に固定された台に置かれ糸の一端をとりつけ，糸の他端には物体Bが鉛直にとりつけられている。はじめ，A，Bは静止しているとして，A，Bがどのような運動をするか調べよ。重力加速度の大きさを g とする。
Ａには，重力Mg，糸の張力T，台からの抗力。Ｂには，重力mgと糸の張力T
手順 ②
Ａは図の右向き，Ｂは鉛直下方を正の向きとする
解 A，Bの加速度を a とすると
Aの運動方程式は Ma＝T
Bの運動方程式は ma＝m g－T
両式からであり，等加速度運動である。
このとき張力T は
AB系で運動方程式をたてると， (M＋m)a＝m g で結果は上記と同じである。
運動方程式を立ててどのような運動かを調べた後，次のような結果のチェックをする
① 両辺の単位チェック(上記の例では，両辺とも加速度の単位になっているか)
② 境界条件を考える(上記の例では，M＝0 とすると a＝g，つまりAがないのだから，Bが自由落下する。m＝0 とするとT＝0になり a＝0つまり動かない)。
例題2 それぞれの質量がm，M の小さな物体A，Bを水平な床の上に静止させ，水平方向に一定の力F を加えた。A，Bの加速度a およびAがBを押す力f を求めよ。A，Bと床との動摩擦係数をμ とする。
解 水平右向きを正の向きにする。A，Bに働く力を右図に示す。N1，N2は垂直抗力である。
Aについて：mα＝F－f－μ mg
Bについて：Mα＝f－μ Mg
両式より
μ ＝0の場合はであり，AがBを押す力 f は摩擦の有無に関係してないことがわかる。
抵抗力を受ける場合の運動
物体が粘性のある媒質中を低速で運動する場合，物体はその速さに比例する抵抗力を受ける。液体中を落下する小球(この場合，浮力も働く)や空気中を落下する雨滴がこれにあたる。飛行機やスカイダイバーが落下する場合には速さの２乗に比例する抵抗力を受ける。
質量mの小球を自由落下し，速さ v に比例する空気抵抗力kvを受けて落下するの運動を考える。小球に働く力は鉛直方向下向きに重力mg，上向きに空気抵抗力kvである。加速度をα とし，下方を正の向きにすると
mα＝mg－kv ∴
空気抵抗がない場合はk＝0としてα＝g の等加速度運動である。空気抵抗力が働く場合は，速さに応じて加速度が変化する運動である。位置を y として，
微分方程式を使って表すと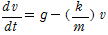
これを積分して
t＝0 で v＝0 だからC2＝g ∴となる。
t ＝ ∞の速さ(終端速度)はである。時間変化のグラフは右図のとおり。位置 y はv を時間について積分して
である。
演習問題 解答
７-２運動方程式
以下の問いで必要なら重力加速度の大きさをg とし、特記なき限り空気抵抗は無視できるものとする。
問41 質量m の小球に軽くて伸びない糸を図のように取りつけ，糸の上端に鉛直方向に一定の力Fを加えた。小球はどのような運動をするか。
問42 図のように質量M の箱の底に質量m の分銅を載せる。これらがそのままの姿勢を保って落下しているとき，
① 空気による摩擦抵抗力 F が箱に働く場合，
② 箱の落下速度が増して空気抵抗力が大きくなり,やがて落下速度が一定になった場合について，分銅の底面に働く抗力を求めよ。
問43 質量2.000[Kg]の上皿式ばねばかりが,質量を無視できる糸で,図のように上皿が水平になるようにつり下げられている。
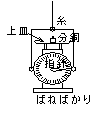g＝9.80[m/s2] とする。ばねばかりの上皿に質量0.500[Kg]の分銅をのせてから，はかり全体を一様な加速度a[m/s2]で鉛直上向きに動かしたため，はかりの指針が0.550[Kg]を指した。a の大きさを求めよ。また，このとき糸の張力はいくらか。
問44 水平と角度θ をなす斜面の最下点から質量mの小物体Aを初速度v0で斜面上方に運動させた。小物体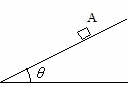
Aと斜面間の運動摩擦係数をμ とする。どのような運動をするか。
問45 天井に固定した，なめらかに動くことのできる小さな滑車に糸をかけ，糸の両端にそれぞれの質量がM，m の小物体A，Bを取りつけて静止させた。
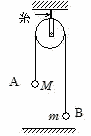Aは始め床から高さhの位置にあった。初速度0でA，Bを動かした場合，どのような運動をするか(これはアトウッドの器械と呼ばれている)。
問46 単位長さ当たりの質量がd [Kg]で，長さが l [m] の一様な棒がある。これをなめらかな水平面上に置き，その右端にF [N] の力を加えるとき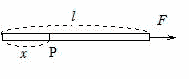
(1) 棒の加速度α は何[m/s2]か。
(2) 左端から x [m] のＰ点での棒に垂直な断面に働く張力Tを求めよ。
(3) x と T の関係を示すグラフを描け。
問47 なめら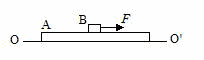
かで水平な床OO'上に，図のように十分長い質量M の板Aが置かれている。さらに，その上に質量m の木片Bが置かれている。板に水平方向の力Ｆを作用させたときの板および木片の運動を力の大きさをいろいろ変えて観察した。板と木片の静止摩擦係数をμ0，運動摩擦係数をμ とする。
(1) F が小さいときには，板と木片は一体になって床に対して同じ速度で運動しはじめた。F が既知として板と木片の加速度を求めよ。
(2) (1)の場合，木片が板から受けた摩擦力の大きさを求めよ。向きも答えよ。
(3) 力をしだいに大きくして，ちょうどF0になったとき，木片が板に対して動き出した。F0を求めよ。
(4) さらに F を上の F0 より大きくしたとき，板と木片はそれぞれ別の加速度αＡ，αＢで運動した。F は既知としてαＡを求めよ。
問48 傾角θ の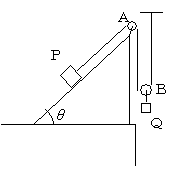
なめらかな斜面上に質量 m の小物体Ｐをのせて，これを糸につけてなめらかな定滑車Aときわめて軽い動滑車Bをへて，他端を天井に固定する。動滑車の両端の糸はともに鉛直とし，また動滑車の中心に糸をつけ，下端に質量
M のおもりQをつるす。
(1) はじめ静止していたPが斜面の上方に動くためには，M，m，θ の間にはどのような関係が必要か。
(2) この条件を満たしている場合，Pの加速度を上向きを正としてa1Qの加速度を下向きを正としてa2，糸の張力をT として
(a) Pについての運動方程式を作れ。
(b) Qについての運動方程式を作れ。
(c) a1とa2の関係式を作れ。
(d) T，a1，a2を求めよ。
問49 図に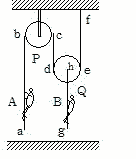
示すように定滑車Ｐおよび質量M の動滑車Ｑに軽い綱abcdef およびgh がとりつけてあり，はじめは静止している。いま，同じ質量m をもつ二人の人Ａ，Ｂがともに地面に静止している状態から同時に綱をよじのぼりはじめる。ＡがＰに対してもつ上向きの加速度をα，ＢがＱに対してもつ上向きの加速度をβ とし，α，β はともに一定であるとする。ただし，ab，cd，efにおける綱の張力は同じ値T であるとし，またghにおける張力をT ' とせよ。
(1) Ａ，ＢおよびＱに対する運動方程式をたてよ。ただし，Ｑの地面に対する加速度をγ とする。
(2) Ｂがのぼりはじめてから時間t ののち，Ｂは地面からどれだけの高さまでのぼっているか。α，β，m，M，g，t のみで表せ。
(3) Ａがのぼりはじめてから時間t の間に，Ａは綱をどれだけの長さたぐり寄せたことになるか。
問 50 質量M の小型リフトの中で，質量m の弾性球が，天井から長さlの糸でつるされている。このリフトにロープをかけ，一定の大きさF［F＞(M+m)g］をもった力で，鉛直上方に引き上げる。弾性球(以下m と略記)は，リフトの床上h の高さにあったとする。糸には質量も伸び縮みもないものとする。
なお加速度の符号は，上向きを正にとるものとし，弾性球の大きさは無視する。
(1) リフトがもつ加速度を，上に与えられた諸量を用いて表せ。
(2) 上で求めた加速度をa で表したとき，m をつるしている糸の張力はどのように表されるか。
(3) 突然糸が切れたとすると，その直後にリフトがもつ加速度a' を求めよ。
(4) 糸が切れてから，m がリフトの床にあたるまでの時間を求めよ。
ホーム メニュー 序論･物理量 ベクトルとスカラー 落体の運動 力 運動の法則 円運動 仕事とエネルギー 運動量
Top
