運動方程式は
mα=F-mg ∴
糸を上向きに引くから、小球が上向きに動くと思うのは早計である。
aの正負では,その後の運動の向きは決められない。
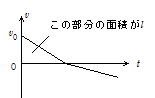
a<0の場合、初速度が負の場合,時刻によって速度vが正,負,0のいずれかになる。
a=0の場合,初速度が0なら常に速度v=0だが,v≠0では初速度のままの等速度運動をする。
問題解答 戻る
問41
小球の加速度をα、鉛直上方を正の向きにする。糸の質量を無視できるから、小球を引く力はF である。小球に働く力はF と重力 mgである。
運動方程式は
mα=F-mg ∴ ![]() 小球は等加速度運動をする。
小球は等加速度運動をする。
糸を上向きに引くから、小球が上向きに動くと思うのは早計である。
aの正負では,その後の運動の向きは決められない。
![]() の場合α >0、
の場合α >0、![]() の場合α=0、
の場合α=0、![]() の場合α <0
の場合α <0
a<0の場合、初速度が負の場合,時刻によって速度vが正,負,0のいずれかになる。
a=0の場合,初速度が0なら常に速度v=0だが,v≠0では初速度のままの等速度運動をする。
問42
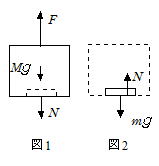
① 分銅が箱から受ける抗力の大きさをN,加速度をα (下向きを正)として,それぞれの運動方程式を立てると,
箱 Mα=Mg+N-F・・・①(図1)
分銅 mα=mg-N ・・・・・・・②(図2)
両式より ![]()
② 等速運動ではα =0だから,②より N=mg (エレベーターは静止しているのと同じ)
問43
分銅に働く力は,はかりから上向きに受ける力(はかりの指針)と下向きの重力だから,上向きを正として分銅についての運動方程式から
0.500a=(0.550-0.500)g=0.050×9.80 ∴ a=0.98[m/s2]
はかり・分銅系で考える。糸の張力をT とすると
(2.000+0.500)a=T-(2.000+0.500)×9.80 ∴ T=26.95[N]![]()
問44
斜面に沿って上方を正の向きにする。Aに働く力は右図のようにmgsinθ,動摩擦力f=μ mgcosθである。
Aの加速度をα とすると,上昇しているときは
mα =-mg (sinθ+μ cosθ) ∴ α =-g (sinθ+μ cosθ) (等加速度運動)
登りうる位置は,最下点からの長さをlとすると,等加速度運動の式(【4】4-3式参照)から
![]()
Aはその後,斜面下方に動き出す。下降する場合の加速度はfの向きが反対になり,加速度α' は
α' =-g (sinθ-μ cosθ) ∴ |α| >|α'| である(右図参照)。
最下点に再びもどったときの速さは(lが等しいから)
![]()
問45
鉛直下向きを正とする。A,Bそれぞれの加速度をα1,α2,糸の張力をT とすると
Aについて:Mα1=Mg-T
Bについて:mα2=mg-T
ここでα1=-α2だから
両式から ![]()
M>m の場合α1>0 (下向きに動く),α2<0,M=mではα1=α2=0である。
(m=0でα1=g,T=0であることを確かめよ)
問46
(1) 棒の全質量はd・l だから,棒全体についての運動方程式は,加速度をα として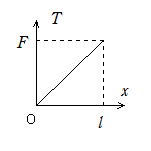
d l・α=F ∴ ![]()
(2) 長さx の部分の質量はd・x だから,この部分についての運動方程式は
dx・α=T ∴ ![]()
(3) T とx は比例関係にあるので右図のようになる。
問47
(1) Mm系での運動方程式を立てる。加速度をα とすると
(M+m)α=F ∴ ![]()
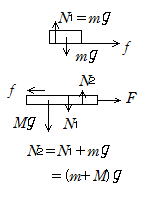
(2) 木片に働く水平方向の力は板からの摩擦力だけだから
mα=f ∴ ![]()
(3) f=f0=μ0N1を越えるとすべり出すから,N1=mg なので(2)から
f0=μ0N1=μ0mg= ![]() ∴ F0=μ0(M+m)g
∴ F0=μ0(M+m)g
(4) 板についての運動方程式は(摩擦力はμ N1=μ mgに変わった)
MαA=F-μ mg ∴ ![]()
問48
(1) つり合いの状態での糸の張力をT0とすると
Pについてのつり合い式は T0=mg sinθ
Qについてのつり合い式は Mg=2T0
両式から M=2msinθ ∴ Pが斜面上方に動くためには M>2msinθ
(2)(a) ma1=T-mg sinθ・・・①
(b) Ma2=Mg-2T ・・・・・・②
(c) Pが斜面に沿って⊿x上がるときQの移動量⊿yの間には ⊿x=2⊿yの関係がある。
よって a1=2a2 ・・・③
(d) ①式を4倍して 4ma1=4T-4mg sinθ・・・①'
②③式から Ma1=2Mg-4T ・・・②'
①'②' 式から
![]() ・・・④ ,
・・・④ , ![]()
①④式から T=m(a1+gsinθ)=![]()
問49
(1) Aについて mα =T-mg (Bの地面に対する加速度をβ ' とすると β '-γ=β γ は上向きを正とする)
Bについて m(β+γ)=T '-mg
Qについて Mγ=2T-T '-Mg
(2) (1)からγ を求め,(1/2)β ' t 2で求める。
(1)より Mγ=2×(mα+mg )-{m(β+γ)+mg }-Mg
整理して (M+m)γ=m(2α-β+g )-Mg
![]()
Bの地面に対する加速度β ' は
![]()
上昇した高さは![]()
(3) Qは(1/2)γ t 2上昇するので,綱は 2×(1/2)γ t 2=γ t 2たぐられる。また,Aは(1/2)α t 2上昇するので,Aがたぐった綱の移動量は
γ t 2+(1/2)α t 2![]()
問50
(1) リフト・弾性球系で考え,加速度をa とすると,運動方程式をたてて
(M+m)a=F-(M+m)g ∴ ![]()
(2) 糸の張力をT として,弾性球について運動方程式をたてて
ma=T-mg ∴ T=m(a+g)
(3) Ma'=F-Mg ![]()
(4) 糸が切れた後の弾性球の加速度は-gでリフトに対する弾性球の加速度は-g-a '
リフトに対しては自由落下するから求める時間をtとすると
![]()