問題解答 戻る
問51
おもりが回転しているときの向心力は![]() で,これがmg を越えると紐は切れる。
で,これがmg を越えると紐は切れる。
![]() =mg ∴ v=
=mg ∴ v=![]()
問52
摩擦力μ Mgが車の向心力より大きくなければすべることになる。その限界値は
![]() =μ mg ∴ μ=
=μ mg ∴ μ=![]()
問53
Oを中心とする円運動をしているから,摩擦力はP→Oの向き。すべり出す直前には 運動方程式から
mrω02=μ mg ∴ ![]()
問54
赤道上の重力は万有引力-自転による遠心力mRω 2,極上では重力=万有引力だから,mRω 2だけ小さい。加速度の減少量は,![]()
これは g の約0.3%にあたる。
問55
①式からr=2Rだから9.8/4=2.5[m/s2]
問56
③式を書き換えて
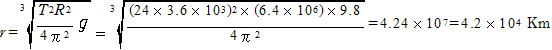
(地表からの高さは3.6×104Km)
問57
(1) 面積速度一定の法則から, 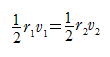 ∴
∴ ![]() =
=![]()
(2) 円運動したときの衛星の速さをvとすると,円運動の運動方程式から
![]()
(3) 衛星の公転周期の軌道は軌道の長半径の2分の3乗に比例するから
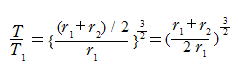
問58
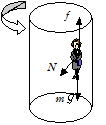
人がローターの壁から受ける垂直抗力をN,人の質量をm,重力加速度の大きさをg とする。床を下げても人が落下しない限界は摩擦力f は最大摩擦力でその大きさはf=μ N=mg である。 ∴ N=mg /μ
ローターの回転数をn,角速度をω とするとω =2πnであり,運動方程式は mrω 2=N=mg / μ
∴ ![]()
問59
水の質量をm,最高点の速さをvとする。水に働く遠心力が重力以上であれば水はこぼれないから,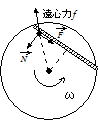
![]() ≧mg ∴ v≧
≧mg ∴ v≧![]()
問60
(1) N+Fの向きが円の中心に向く。 (![]() )
)
観測者が円板の上に立った場合 ![]() になる。
になる。
(2) 小物体の円運動の半径はで(2)の3力はつり合っているから![]()
Nの方向について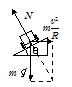
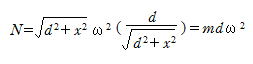
F方向について 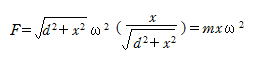
問61
電車系で考えると,路面からの垂直抗力Nと電車の重力mgの合力Fが向心力となり円運動する。これと遠心力がつり合いの関係にあればよい。
図より ![]()
![]()
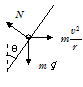
問62
小球には重力mg,垂直抗力N,遠心力![]() がはたらき,この3力がつり合っている。水平,鉛直方向の力のつり合い式は
がはたらき,この3力がつり合っている。水平,鉛直方向の力のつり合い式は
![]() ∴
∴ ![]()
問63
PQがO点より左側にx だけ変位したときPQに働く力は下図の通りである。PQの加速度をβとすると
![]()
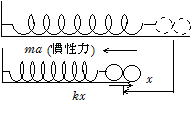
これは ![]() つまり
つまり ![]() の周期で
の周期で
![]() を中心とする単振動を表す。
を中心とする単振動を表す。
振幅A は ![]() (a=g とすれば鉛直ばねである)
(a=g とすれば鉛直ばねである)
また,Pが最初にx=0に戻って来るまでの時間は1周期の時間だから ![]()
問64
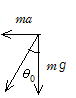
振り子を電車内から見ると重力mg,慣性力mα が働いている。この2力の合力は![]() でこの合力と鉛直線がなす角度をθ0 とすると
でこの合力と鉛直線がなす角度をθ0 とすると ![]() である。題意により α ≪だからθ0≒
である。題意により α ≪だからθ0≒![]()
見かけ上の重力加速度は ![]() になるので
になるので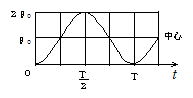
周期 ![]()
θ の時間変化のグラフは右図のようになる。
問65
(1) 力のつり合いから
mg=kx0 ∴ ![]() [m]
[m]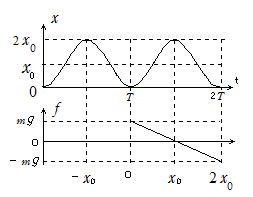
(2)(3) x>0で f <0, x <0で f >0
加速度をaとしてBについて運動方程式をたてると
ma=mg-kx ![]()
∴ x=x0を中心とする単振動をする。
![]() (α は位相角)
(α は位相角)
t=0 で x=0 ∴ ![]()
![]()
また f=ma=-k(x-x0)なのでf は直線
x=0で kx0=mg,x=x0で f=0,x=2x0で-kx0=-mg
問66
(1) 小球に働く遠心力はmxω 2,復元力はkxである。
(2) 合力は mxω 2-kx
(3) 微小振動するための条件は,合力が常にO点に向かうことである。
∴ mxω 2-kx<0 ∴mω 2-k<0 (または,![]() ) (4) (3)の条件のあることが単振動する条件である。
) (4) (3)の条件のあることが単振動する条件である。
このとき合力Fは一般にF=-mx(ω ')2 (ω ' は角振動数)
F=-mx(ω ' )2=-(k-mω 2)x ∴ ![]()
単振動の振動数をn',円管の回転数をnとすると
ω '=2πn',ω =2πnだから ![]()
ここで,n=1(円管が1回転)のときのn' は![]() [回]
[回]
(円管のω とばね振動の角振動数ω ' は全く別のものである。混同しないこと)
問67
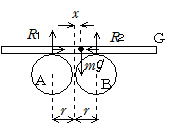
棒の重心が両円筒の中央よりx だけ右へ偏った点を通過するとき,棒に働くA,Bからの垂直抗力R1,R2の大きさは
鉛直方向の力のつり合いから R1+R2-mg=0
重心Gに対する力のモーメントのつり合いから
R2(r-x)-R1(r+x)=0
両式から ![]()
棒がA,Bから受ける摩擦力の向きと大きさは
Aから受ける動摩擦力は右向きでその大きさはμ R1である。 μ R1=![]()
Bから受ける動摩擦力は左向きでその大きさはμ R2である。μ R2=![]()
棒に働く水平方向の合力Fはμ (R1-R2)=-![]()
![]() は定数だから F は-xに比例する力なので,単振動していることがわかる。
は定数だから F は-xに比例する力なので,単振動していることがわかる。