ホーム  メニュー            電子と光    波動性と粒子性    原子構造   原子核   核分裂核融合   クォーク
                                                                             

【２２】波動性と粒子性(前期量子論)
  １ 光の粒子性(particle nature of light)

金属に光を当てると電子が飛び出す現象を光電効果(photo electric effect)という。図1のように真空管の中の電極A，Bに電圧をかけられるようにする。
 A，B の電位をそれぞれV_A，V_B とする。
 　光の強さを一定にして，極板Aに光の波長を変化させて当てた場合，図2のような結果が得られた。つまり，V_A＜V_Bの場合は波長に関係なく一定値となるが，V_A＞V_Bでは回路を流れる電流(光電流)が0になるときのAとBの電位差V₀は，波長が短いほど小さくなる(絶対値は大きくなる)。Aから飛び出した光電子は，AB間の電位差が小さいとBに達することができるが，電位差が大きくなると(AB間の電界が光電子にする仕事はeV)，やがて光電子はBに達することができなくなるので，
eV₀(e＝電子の電荷)が光電子の持つ最大のエネルギーである。V₀の意味は，Aから飛び出した光電子をBに達することを阻止する電位差ということができる。
   つぎに波長λを一定にして，明るさを変化させると図3の結果が得られた。つまり，V₀は明るさに関係なく，明るくなるほど光電流が増加することがわかる。光電流が大きいということは，光電子の数が多いということだから，明るいほどAから飛び出す電子の数は多いということである。
  図2の結果から，横軸に光の振動数ν，縦軸を光電子の最大エネルギー(K₀＝eV₀＝  m：電子の質量，v：光電子の速度)としてグラフを描く(図4)。ある振動数ν (＝c/λ，c＝光速度)の光を電極Aに当て，そのときのV₀からeV₀を縦軸としてグラフを描く。グラフ中のν₀は限界振動数と呼ばれ，光電子が飛び出す限界の光の振動数である(このときの波長λ₀を限界波長という)。光の振動数がν₀より小さいと(波長が長いと)光電子が飛び出さない，つまり光電効果は起こらないことを示す。
   図4からわかることは，電極Aの金属の種類を変えてもグラフの傾きは変わらない。またグラフは直線になるのでνが0のときの縦軸の値W(これを仕事関数という)は電極Aの金属の種類によって決まる固有のものであることがわかった。仕事関数は，光電子を物体表面まで移動させるのに必要な仕事である。
                             
Lenardなどの詳細な実験結果からわかったことは以下の通りであった。

(1) 光電子は陰極金属固有の振動数ν₀より小さいと飛び出さない。
(2) 光電子のエネルギーはνが大きいと増加する。
(3) 弱い光でもν＞ν₀だと光電子がすぐに 飛び出す。
(4) ν が一定の場合，光電子数は，光の強さに比例する。

光を波動と考えた場合，次の矛盾点がある。

(a) 光のエネルギーは振幅が大きい(明るい)と大であり( 「波の性質」「波の強さ」参照)，光電子のエネルギーの大きさ，飛び出す条件(1)，(2)に矛盾する。
(b) 光が弱いと，光電子が飛び出すのに時間がかかるはずである。弱い光ではすぐに光電子が出ないはずなのに(3)と矛盾する。     

これらの結果に対して，アインシュタインの光粒子説が1905年に提案された。

「振動数ν の電磁波をhν のエネルギーをもつ多数の粒子(光子(photon)，光量子(light quantum))の流れとみなし，その1個が電子に衝突してすべてエネルギーを与える」 (hはプランク定数＝6.6×10^-34 J･s)

というものであり，光子1個のエネルギーがhνであり，金属に光子が衝突すると金属表面に電子を移動させるためにWの仕事(仕事関数)を要し，残りのエネルギーが金属から飛び出す光電子のエネルギーK₀である(hν＜Wなら光電効果は起こらない)。
これを式で表すと
         hν＝K₀＋W    (22-1)
K₀＝0 のとき，hν₀＝W だから，限界振動数は，限界波長は である。
また，図4のグラフの傾きはhν＝K₀＋W(＝hν₀)から， つまり，縦軸の単位をJとするとプランク定数を示す。

仕事関数，エネルギーの単位はeV(＝electron Volt 電子ボルト)を使う。電子ボルトは，１個の電子に1Vの電位差を与えたときに得られるエネルギーであり，
    1eV＝1(V)×(1.6×10^-19C)＝1.6×10^-19 J である。
 [注] (eVは単位であるが，光電子の最大エネルギーで出てきたK₀＝eV₀のeV₀は電気素量eと電位差V₀の積である)   

仕事関数(work function )W と限界波長λ₀の例

	W(eV)	λ0(10-7m)
Cs	1.9	6.5
Na	2.3	5.4
Zn	4.2	3.0
W	4.5	2.8
Pt	5.3	2.3

表の下に行くほどW が大きいから光電効果が起こりにくい。
可視光線ではCsとNaだけ光電効果が起こることがわかる。





例
(1) Naの波長λ＝5.9×10^-7m とすると，この光の光子1個のエネルギーは何eVか。
(2) この光が1Wで出されている場合，毎秒何個の光子が出ているか。
ただし，光速度c＝3.0×10⁸m/sとする。

解
(1) E＝hν＝hc/λ＝(6.6×10^-34)×(3.0×10⁸)/5.9×10^-7＝3.36×10^-19J＝3.36×10^-19/1.6×10^-19＝2.1eV
(2) 1.0(J/s)＝N×(3.36×10^-19)      ∴  N＝3.0×10¹⁸個/s      (1W＝1J/sである)

実験結果(3)「 弱い光でもν＞ν₀だと光電子がすぐに 飛び出す」についての説明
1W(＝J/s)の点光源が3次元で光を出している場合を考える。
半径R＝1mの球面上を毎秒通過するエネルギーE(J/m²･s)は   1(J･s)/4π×1²(m²)＝1/4π(J/m²･s)
表面上の断面積S(m2)では毎秒S/4π(J/s) ･･･�@
原子半径r＝0.5Å＝0.5×10^-10mとすると，その断面積はS＝π×(0.5×10^-10)²
光電子のエネルギーは0.1eV＝10^-20Jの大きさなので，これを原子が受け取る時間t(s)は
                             
   この結果，光を波と考えると1Wの光を原子が受け取るのに要する時間が瞬間でないことが容易に理解できる。

光電効果についての歴史

1888年 ハルバックス(L.F.Halwacks1859-1922独) 亜鉛球に紫外線を当て光電効果発見。ストレトフ(Aleksandr G.Stoletov1839-1896露)が
　　　　　詳細に検証。
1887年 ヘルツ(H.R.Herz1857〜1894独) 火花放電が紫外線の方が起こりやすいことを発見
1902年 レナート(P.E.A.Lenard 1862-1947) 金属の種類によって光電効果のしきい値がことなることを発見
1905年 アインシュタイン(A.Einstein 1897-1955独) 光量子説
1905年 ミリカン(R.A.Millikan) 光電効果の実験からプランク定数を測定した

２ X線(X ray)の二重性

X線は波長が10^-12〜10^-8mの電磁波である。1895年レントゲン(1845-1923)によって発見された。
(1) X線の発生
フィラメントFを熱してカソードから熱電子を発生させる。アノードにはW，Mo，Fe，Al，Pbなどを用いる。アノードA(陽極)とカソードK(陰極)間に電位差Vをかけて電子を加速しアノードに衝突させる。アノードに衝突した電子は制動放射によってX線が発生する。熱電子はフィラメントが高温なほど多く，電位差Vが大きいほど波長の短いX線が発生する。
  V＝50〜100KVが医療用，V＝１５０〜400KVが非破壊試験用，50〜200KVが厚み計測に用いられ，波長の短いX線を硬いX線，波長の短いX線を柔らかいX線ということがある。




(2) X線の性質
    直進し，物質への透過力大，写真フィルムを感光させる。
    気体を電離し，蛍光物質を蛍光させる。
(3) X線のスペクトル
加速された電子は電場からeVのエネルギーを与えれられる。X線も光と同じくE＝hνの光子と考えると
     eV−E '＝hν (E ' は発熱などによるエネルギーロス)
eV が一定でもE ' が連続ならば振動数νも連続的になる。これが連続X線である。
左図にあるように加速電圧Vが大きいと最小の波長 λ₀が小さくなる。λ₀は電場が電子に与えたエネルギー
eV がすべてX線のエネルギーhνになる場合であり，E '＝0だから，
     eV＝hν＝       ∴  最短波長  (22-2)
    これから  ∝  

(4) X線の波動性(wave nature of X ray)

1898年 Haga，Windによってスリットの回折干渉像が得られた。波長は10^-10m程度であった。
1912年 ラウェ硫化亜鉛結晶にX線を当て，回折模様を撮影した。
1912年 Bragg父子によるX線干渉によりブラッグ反射を発見。
デバイシェラー(Debye scherrer1884-1966)法
   X線を左図のように結晶構造の物質に当て，円周上に達する散乱X線の干渉像を測定し，結晶の大きさなどを測定することができる。
粉末結晶法と呼ばれるものの利点は，良質の結晶を必要としない。結晶格子面が複数存在するので，入射線は多くの微結晶のうち，ブラッグ反射の条件を満たす。
  入射X線と 2θの角をなす円錐面に沿って現れものをデバイシェラー環という。左下図のd，d'，d''を測定することにより結晶構造を特定することができる。

         (5) X線の粒子性(particle nature of X ray)

コンプトン効果 1923(A.H.Compton1892-1962)
X線を結晶構造の物質に当て，入射角を変えていき，どのような散乱(反射)X線が現れるかを測定する。
下図はモリブデン電極から出されたX線を石墨片に当てた結果で，θ は散乱角である。
         
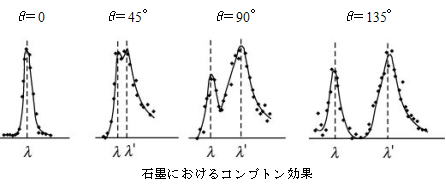
実験結果は以下のようであった。
�@ 散乱線の中に入射X線(波長λ)より波長の長いもの(波長λ')が存在する。
�A そのずれの大きさは，散乱角θ に依存する。θ が大きいほど波長のずれ��λは大きい。
�B 散乱角θが大きくなると波長のずれのないX線の強度は減少し，ずれたX線の強度は大きくなる。

このように，散乱X線の中に波長の異なるX線が現れる現象をコンプトン効果という。
この現象は，光の場合で考えると入射光の波長に対して反射光の波長が長くなって反射して色が変化するということであり，X線を波動と考えたのでは説明がつかない。

コンプトン効果の理論
電磁波はE＝hν＝のエネルギーをもつとともにの運動量をもつ光子との考えをX線に適応した。
質量mの静止している電子にX線が衝突し，電子を速さv，入射X線の方向と角度θで反跳し，散乱X線は角度φに進むものと考える。これらの衝突は弾性衝突と考える。
入射X線のエネルギー＝，運動量＝，散乱X線のエネルギー＝，運動量＝，電子の運動エネルギー＝，運動量＝mvとする。
エネルギー保存の法則は
   ＝＋ ･･･(1)     (22-3)
入射X線の方向とこれに垂直な方向の運動量保存の法則は
       ＝cosφ＋mvcosθ ･･･(2)       (22-4)
       0＝sinφ−mvsinθ  ････(3)        (22-5)
(2)，(3)式から
       ･･･(4)
(1)式から
                 ･･････(5)
(4)＝(5)から
　　
    λ≒λ' として
          (22-6)
これを横軸φ，縦軸��λにして描いたものが右図である。
  をコンプトン波長という。
グラフから，φが大きいと��λが大きくなり，実験結果�@，�Aと一致する。 

光子の運動量がである理由

 １辺Lの立方体中に光子が１個あった場合，光速をc，x方向の成分をc_xとする。
   時間1(s)間あたりに光子が壁ABに衝突する回数は
1回の衝突での運動量変化は2p_x
時間1(s)間に壁ABに与える運動量は  (＝平均の力)
光子1個による，ABの圧力p₁は  p₁＝
N個の光子では，p＝    (＜Pxcx＞は平均を表す)
空洞の光のエネルギー密度U(J／m³)と圧力Pには  P＝U/3 の関係がある。
また，だから，等方性から を考慮して
 
   　　  ∴                           

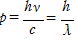
古典論での��λはλ≒λ' と近似したが，相対論(高校では出てこない内容)では近似をすることなく求められる。

特殊相対論によると，電子の静止質量をm，速度をv，エネルギーをE，運動量をp，光速をcとすると
     
エネルギー保存の法則は
     ＋＝＋E ･････(1) '
運動量保存の法則は
     ＝cosφ＋pcosθ ･････(2) '
     0＝sinφ−psinθ   ･･････(3) '
(2)'，(3)'から
      ･････(4)'
(1)’から
       ･･･････････(5)'
(4)'，(5)’から
       ･･･････(6)'
       ∴     ･･(7)'
(6)'，(7)'から
    ･････････････(8)’
(1)'，(8)'から
     

3 電子の波動性(wave nature of electron)

電子の粒子性は陰極線実験などから知られたが，1921年頃からエルザッサー(W.Elsasser1904-1991)，デビソン(C.J.Davisson1881-1958)，クンスマン(C.H.Kunsman)らによって低エネルギー電子線の白金版による実験で電子の回折像を発見。電子波の結晶格子による回折と考えた。
1927 デビソンとジャーマー(L.H.Germer 1881-1971) Ni の単結晶で検証(右図)
1927 トムソン(G.P.Thomson＝J.J.Thomsonの息子)はセルロイド，金，アルミニウムの薄膜(1mm程度)で散乱陰極線の回折実験で電子線のデバイシェラー環を検証
1928 菊池正士(1902-1974)薄い雲母単結晶で透過電子線の干渉像(菊池図形と称する)を検証

上記の諸実験から，電子が波動性をもっていることがわかった。ド･ブロイ(L.V.de Broglie1892-1987)は電子だけでなく物質すべてについて以下の波動性をもっていると考えた。
量子仮説から  運動量 p＝ から，物質波の波長は
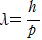
電子では  p＝mv から であり，V0(V)で加速した場合，電子の速度vは
        eV0＝      ∴   v＝
        ∴          (22-7)

相対性理論によると，静止質量m0の電子が速さvで動いていると，光速をc とすると，
静止エネルギー＝m₀c²である。
質量m＝ () だから ，エネルギーは  
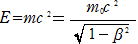
運動エネルギーKは
     
ここでβ≪1 の場合は (古典論との比較)
     
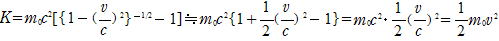
また，運動量pは
      これを書き直して
     
     ∴    

光子と電子の比較
               運動量         波長        エネルギー
  光子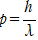                      E＝hν
  電子       p＝mv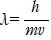               (相対論では)

粒子，波動性の並行性
(1) 光が屈折する場合
    波長をλ，λ '，速さをc，c '，入射角，反射角をぞれぞれθ，θ ' とすると，屈折の法則から
         θ＞θ ' なら c＞c '，λ＞λ ' (c，c' は位相速度)  ･･･�@
(2) 光を粒子と考え，それぞれの運動量をp，p ' とすると，境界方向の運動量は変わらないから
psinθ＝p ' sinθ'
∴    ･･･ �A
ここでニュートンが考えた粒子として考え，その速度をv とすると
p＝mv，p '＝mv '
∴     ･･･ �B
    → 屈折率は�@と�Bを比べると速度の比は逆である。
        ∵  v，v ' は粒子の速度であってc，c ' の位相速度ではない。
    次に光を光子で考えると
        ， これを�Aに代入すると となり，�@と一致することがわかる。
   物質波の速度vは物質波がλが異なるパルス波の集合と考えられるので群速度(λが異なる波速全体の速さ)であり，v＝ν λ が成り立つ
   位相速度と一般には異なる。
   ⇒ 電子波を考えるときは，�B式で考えてはいけない。

 

ホーム  メニュー            電子と光    波動性と粒子性    原子構造   原子核   核分裂核融合   クォーク

           Top