�z�[�� ���j���[ ![]() �d�q�ƌ� �g�����Ɨ��q�� ���q�\�� ���q�j �j����j�Z�� �N�H�[�N
�d�q�ƌ� �g�����Ɨ��q�� ���q�\�� ���q�j �j����j�Z�� �N�H�[�N
�y�Q�P�z �d�q�ƌ�
�Q�P�|�P�d�q�̔�d��(specific charge of electron)
�� �d�q�͂ǂ̂悤�ɒ��ׂ�ꂽ��
�d�q(electron)�̌ď̂�G.J.�X�g�[�j�[(1826-1911)��1891�N�ɓ��������B
�d�q�̑��݂͐^����d�̎����ɂ���Ĕ������ꂽ�B19���I�����ȍ~�s���S�^��̕��d���������ꂽ�BA.P.�}�\��(1806-1858)�͋��͂ȃR�C���ƃg���`�F���̐^��Ǔ��Ŏ��������B���N�̌�K���X���H�ł�����H.�K�C�X���[(1814-1879)�����I�ȃK���X���d�ǂ��쐬�����B�K�C�X���[�ǂ͐�cm�`��mmHg�Ńl�I���T�C���Ȃǂ̕��d�ǂł���B�C�̂ɂ���ĐF���قȂ�C�u�����͏��ʂ�Ar�CHg���C�������ǂɌu��������h�莇�O���ɂ���Ĕ�������B�K�C�X���[�ǂ̕��d�ɂ���ĉA�ɐ��߂����ΐF�Ɍ����邪�^��x�ɂ���ĊǓ��̖͗l���قȂ�B
���̊ǂ��K�C�X���[�ǂƃv�����b�J�[(1801-1868)�������B�����̊Ǔ��ōs������d�́C���ɔ��������̂��������C�d�C��C�̗̂��_����w�[�����ɂ߂�Ƃ����_�ł́C���܂�𗧂��Ȃ������B����|���v�����P����C��荂�x�̊�(�^��)�����B�������悤�ɂȂ�ƁC���d���ۂ�L���ɗ��p�ł���͈͂���i�ƍL�����̂ɂȂ����BJ.W.�q�b�g���t(1824-1914)��1869�N�ɊǓ��̈Â���ԕ������r�C���i�ނɂ�čL����C���ɂ͊ǑS�̂������Ƃ��m�F�����B1869�N�q�b�g���t�͂��̌u������K���X�ǂƉA�ɂƂ̊Ԃɕ��̂�u���ƕ��̂̉e�������邱�Ƃ��ώ@���C�A�ɂ���o�Ă�����ː����u���̌������ƍl�����B���̕��ː����S���h�V���^�C����1876�N�Ɂu�A�ɐ��v�Ɩ��������B
�N���b�N�X�͉A�ɐ����C�K���X�ǂɓ��ꂽ�H���Ԃ���]�����邱�Ƃ��C����̉e�����邱�Ƃ���A�ɂŕ��d�ׂ�������C�̕��q���A�ɐ����Ǝ咣�����B����C�g�������Ƃ闧��̉Ȋw�҂����́C�u�G�[�e��(����`����}����17���I�ɓ������ꂽ)�v�̐U�����A�ɐ����ƍl�����B���̍����́C�Ód��������Ă��A�ɐ��͋Ȃ�Ȃ��Ƃ����w���c�̎����C�����̔������A�ɐ����ʂ����[�i���g�̎����������Ƃ��Ă����B
�@J.J.�g���\���͎��ŋȂ����A�ɐ������d��ɓ����Ă����d�ׂ����o����邱�Ƃ������āC�דd���q���̂��̂��A�ɐ��ł���Ƃ����B�܂��C�w���c�̎����ɑ��ẮC�A�ɐ��ɂ���ċC�̕��q���d�������ƁC�d�ɕt�߂ɂ͂��̔��Γd�ׂ����C�I�����W�܂�C�d�C�I�ɒ��a����Ď��ۂ͓d�ꂪ���݂��Ȃ����ƂɂȂ�ƍl�����B�C�̕��q�����Ȃ����邽�߂ɐ^��x�������Ď��������Ƃ���C�킸��2V�̐Ód��ʼnA�ɐ����Ȃ��邱�Ƃɐ��������B�g���\���͋����Ɏ��O�����Ǝ˂����Ƃ��ɂƂяo���דd���q���A�ɐ����q�̑�p�Ƃ��Ďg���ĉA�ɐ����q�̎��ʂ𑪒肵���B���̎��ʂ͐��f�C�I�����������Ə��������Ƃ��킩��C1899�N�C�u���q�͑����́f�����q�f���琬���Ă���v�Ƃ��C�ŏ��̓d�ׂƍl�����Ă������f�C�I���̓d�ׂƁC�A�ɐ����q�̓d�ׂ̓��������Ƃ������ꂽ�B���ēd�C�f�ʂƂ����Ӗ������߂��X�g�[�j�[�̑���ł���g�d�q�h���������C�g���\���́f�����q�f�͓d�q�ƌĂ��悤�ɂȂ����B
�@�@����38�N�i1905�N�j�ɋߓ��k���ɂ��w�d�C�w�u�`�x�ŁC�A�ɐ��͓d�C��тт��u�ɔ����́i�d�f�j�v�ƋL����Ă���B
(1) �d��E�ɂ��d�q�̐U�镑��(�d�ׂ�e�C���ʂ�m�Ƃ��C�d�͂ɂ��e���͂Ȃ����̂Ƃ���)
�}�̂悤�ɋɔԊud�C����l �̃R���f���T�[�ɓd�ʍ�V �������C�d�q��d��(E��V/d)�ɐ��������ɑ���v0�œ��˂�����B���s�d�ɔ̒��S����u���ʂ܂ł̋�����L�Ƃ���B�d�q�͓d�����ʉ߂�����C�u���ɋP�_�����B
x y�������ꂼ��̉^����
�}�̗̈�(�T)
�@�@x���� ����vx��v0�C�ړ����� x��v0t �@ (l��v0t0)
�@�@y���� �����x��ay�^�������� may��eE ��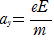
�@�@�@�@�@�@�@vy��ayt�C�ړ����� y���A
���s�d�ɔ̉E�[�ł�
�B (21-1)
�� x��0�`l �ł͕����^��
�̈�(�U) �d�q�͗͂��Ȃ��̂œ����x�^��������B���̂��ߒ����^���ł���B
�@�@�@�@�@�@�����́@vx'��v0�Cvy'��vy
�@�@�@�@�@�@�ړ��������C
�u���ʏ�̈ړ�������
�@�@y��y1�{y2����
�D (21-2)
�� �d�q�̏����xv0��V0(V)�ʼn��������
�@�@�@�@�@�@�E
�@�@�@�������L��e/m�̎��ɑ������ƁCe/m���������ꑪ��s�\�Ȃ̂ŁC���̎��E���̑���ƍ��킹��e/m�����߂�B
(2) ���E���̓d�q�̐U�镑�����̒���l �̗̈�Ɏ��ʎ�O���牜��������l�Ȏ��EB������B�}�̂悤�ɏ����xv0�œd�q�𑗂荞�ނƁC���E���ʼn~�^���C���E���o�Ă��璼���^������B���E���̈ړ�����z1�C���E�O�̈ړ�������z2�Ƃ���B
���E���ł̓��[�����c�͂����S�͂ƂȂ�~�^�������邩��C���a��r�Ƃ��ĉ^������������
�@
�A
���E���o�Ă���͊O�͂��Ȃ����璼���^��������B
���B
�� z��z1�{z2���C (21-3)
�C����(1)�E����v0���������e/m�����߂���B
�����œd����ɂ����āC�@��y ��z �����l�ɂ����
�@�@�@
�C������
����Ƈ@������
(21-4)
E �� B���ɂ������ꍇ�̓d�q�̋O�Ղ��E�}�Ɏ����B�������ɂȂ��Ă��邱�Ƃ��킩��B
�d�C�f�ʂ̑���(elementary electric charge) Millikan(1868-1953)�ɂ��
�P�������ɋɔ𐅕��ɐݒu���C�d���^������悤�ɂ��Ă����B�㕔������H�𗎉������C���H��d�������邽�߂�X�����Ǝ˂���B�������Ă�����H�̑��x���������ő��肷��B���H�̓d�ׂ�q�C���ʂ�m�Ƃ���B
�d��������Ȃ��ꍇ�C���H�͋�C��R���Ē����ɓ����������x������B���̂Ƃ��̑��x��v1�Ƃ���ƁC�d��mg�Ƌ�C��R��kv1�̂荇������
mg��kv1 (k�͖��H�ɂ���Č��܂�萔) �@
�d��E���������ꍇ�C���H�ɓ����͂��荇���ē���v2�ŏ㏸����B�Ód�C��qE��������C��C��R��kv2�C�d��mg���������Ɏ�̂ŁC�͂̂荇������
�@�@qE��kv2�{mg �A
�@�C�A������
qE��k(v1�{v2)�@�@�@�� q���B (21-5)
�萔k�͇@������H�̎��ʂ����m�Ȃ�v1�𑪒肷��Η^������B
����ɂ��Ɠd��q�͂���d�ׂ̐����{�ł��邱�Ƃ��킩�����B
�����
�@�@�@�@�@�d�� q1 q2 q3 q4 q5
�@�@�@�@�@�@�@�@�@11.36 9.70�@�@8.09�@�@4.87�@�@3.23�@�~10-19C �� ����l
N�e �@7e 6e 5e 3e 2e �@ �� q ���d�C�f��e�̉��{���ׂ�
�� e�����d��/�d�q��
�@�@�v�����N(E.K.E.L.Plank)�萔�͂ǂ����痈����
��L��k��ʂ̕��@�Œ��ׂĂ݂�B���H�̔��ar�C��C��R�ɊW����S���W�������l������ĂȂ��B�����ŁC�������l�����ꍇ�ǂ��Ȃ邩���l���Ă݂�B
�@�X�g�[�N�X�̖@������C��R�͂�F��6��r��v (�������C���̎���r ���������Ǝg���Ȃ�)
�@���� F��kv1��6��r��v1��mg ��
���� k��6��r����
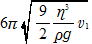
�B�������������C
���͂��l������ƁC���́�����
�㎮�̃ς��ρ|��0�ƒu��������
�D �� ����q�Ȃ� q��(v1�{v2)
�d��q��q' �ɕω�������v2��v2' �ɕω������
�� ��q��q�|q '���E
�v�����N�萔�͍����t�˖�肩��o�������B
�����}�[(Lummer)�ƃv���O�X�n�C��(Pringsheim)�ɂ���Ă͂��߂Ē��ׂ��č��ꂽ����(�S�Ă̓d���g���z�����闝�z�I�ȕ���)�̎����ɂ��C���̂����˂���d���g�̔g���Ɠd���g�̋����ƍ��̂̉��x�̊W���E�}�̂悤�ȃO���t�������C����ɑ���莮�����e�팟�����ꂽ�B���̂̔g���ɑ�����˂��銄��E�͔g���ɂƉ��xT�̊��ł���B�@ Wien�̎�(1896�N)
(21-6)
�A Rayleigh-Jeans�̎�(1900�N)
(21-7)
�B Plank�̎�(1900�N)
(21-8)
Wien��Rayleigh(1842 - 1919)-Jeans(1877 - 1946)�̎��̓����}�[�ƃv���O�X�n�C���̎������ʂƔ�ׂ�ƁC����͈͂ł͈�v���邪���ׂĂ�ԗ�������̂ł͂Ȃ��������C�v�����N�̎��͏�L�̎���a��2��c2h�Cb��ch/k�@�Ɓ@(h�̓v�����N�萔�ł����ł͂��߂Ē��ꂽ�����ʂł���)�@����ƃO���t�Ƃ悭��v�����B�����ɂ͂��߂ăv�����N�萔h�ɈӖ�������C���G�l���M�[����̎��R�x�ɕ��z�����l�͈قȂ�U�����˂ɑ��ē������Ȃ����Ƃ������B(�U�����˂̌������˥�z�������Ƃ��Ch�˂̐����l�̃G�l���M�[�����˥�z�������ƍl����)
���� h ���C��Ɍ��d���ʂ����������ɂ��āC���q�̐��E���x�z���Ă��邱�Ƃ��𖾂���Ă����B
�����t�˂̎������玟�̖@�������������ꂽ�B
(1) Wien�̕ψʂ̖@��
�E��O���t�̂��ꂼ��̉��xT�ƃG�l���M�[�̍ő�������Ƃ��̔g����max�̊Ԃ̊W���͎����ŗ^������B
��max�T��2.87�~10-3 m�K (21-9)
���˂����d���g�̔g���́C���̂̎�ނɂ�炸���x�����Ō��߂���B���̎�����C���̂�������d���g�̔g�����牷�x�𑪒�ł���B
(2) Stephan�|Bolzman�̖@��
���˂����d���g�̑��G�l���M�[�͉��x��4��ɔ�Ⴗ��B���̕\��1m2����1�b�Ԃɕ��˂����G�l���M�[��
E����T 4��5.67�~10-8T 4 J/m2�s (21-10)
����E��[�g��]�ŏo�Ă����g�̋����Ɠ����ł���B(�n����C�ɓ���O��1cm2��1���Ԃɑ��z����^������G�l���M�[�z�萔�Ƃ���)
(1)�̗�
���z�ł̓�max��5.0�~10-7m ������C���z�̕\�ʉ��xT��
(2)�̗�
���z����̒n���ւ̕��˃G�l���M�[��3.25�~102 cal/m2�s������C���z�ƒn���O�̋����͑��z�̔��aR��215�{�Ƃ���
�n����C�ɓ���O�ɒP�ʎ��Ԃɑ�����G�l���M�[��
E1��3.25�~102�~4���~(215R)2�~4.19 (J/s) (4.19�͔M�̎d������)
���z����P�ʎ��Ԃɕ��˂����G�l���M�[��Stephan�|Bolzman�̖@������
E2��(5.67�~10-8)T4�~(4��R2) (J/s)
E1��E2���� T��5.77�~103K
�z�[�� ���j���[ �d�q�ƌ� �g�����Ɨ��q�� ���q�\�� ���q�j �j����j�Z�� �N�H�[�N