�z�[�� ���j���[ ![]() �d�q�ƌ� �g�����Ɨ��q�� ���q�\�� ���q�j �j����j�Z�� �N�H�[�N
�d�q�ƌ� �g�����Ɨ��q�� ���q�\�� ���q�j �j����j�Z�� �N�H�[�N
�y�Q�U�z �N�H�[�N(quark)
�P.�f���q(elementary particle)
�����̍\���v�f�ƍl�����闱�q��f���q�Ƃ����B�f���q�̓Q�[�W���q�i���q�Ȃ�)�C���v�g��(�d�q�̒���)�C�n�h����(�z�q�C�����q�C���Ԏq�Ȃǥ��N�H�[�N����Ȃ�)�ɑ�ʂ����B
�f���q�����ׂ�ꂽ�͂��߂́C�d�q(1897�N)�C���C�z�q(1915-1919�N)�ɑ����Ē����q(1932�N)�C���Ԏq����(1935�N)�C�����Ԏq(1937�N)�C�����Ԏq(1947�N)�Ȃǂ̔����ɂ��f���q�̕���C�����@�\�C�ʎq�_�̊����ł������B���̌ア�낢��Ȓ��Ԏq����������C���ݍ�p�����\�̂悤�ɕ��ނ���邱�Ƃ��킩�����B
| �� | ���� | ��p���a | �Q�[�W���q | �Ώ� |
| ���L���� | �P�O�|40 | �� | �d�͎q(�������) | |
| �d���� | �P�O�|2 | �� | ���q(̫��) | �j�Ɠd�q�� |
| ������ | 1 | �P�O�|13���� | �O���[�I�� | �n�h������ |
| �ア�� | �P�O�|5 | �P�O�|16���� | �v�}�C�y�O | ���C��ҿ݂Ȃǂ̕��� |
�����āC�f���q�̑Ώ̐��C�f���q�̐F���N�H�[�N���O���I����ʂ��Ă̗ʎq�F�͊w���l�����C1964 �N�ɃQ���}��(M.G.Gell-Mann1929-)��ɂ���ăN�H�[�N���_���l�����C1960�N�㖖���瓝��ꗝ�_���l���o����Ă������������_�����Ă��Ȃ��B
�f���q�̕���
�@�@�� �f���q�͕\�L�̑��Ɍ��݂ł͖�Q�O�O��ނ��m�F����Ă���
| �� | ���@�@�� | ���q | ���� | |||
| �� �v �g �� |
��(�d�q)�j���[�g���m | ����(�d��0) | 1/2 | 1931�߳�,̪�Д����B�������q�B���ʂقƂ�ǂȂ��B�ア���ݍ�p�����Ȃ��̂ŕ����߂���B | ||
| ��(�~���[)�j���[�g���m | ����(�d��0) | 1/2 | ||||
| ��(�^�E)�j���[�g���m | ����(�d��0) | 1/2 | ||||
| �d�q�� | ���|(�d�ׁ|��) | 1/2 | ���|��1897�ѿ�,���{��1932���ް�� | |||
| �~���[�I��(�~���[���Ԏq) | ���|(�d�ׁ|��) | 1/2 | 1947�߳�� | |||
| ��(�^�E)���q | �с@(�d�ׁ|��) | 1/2 | 1975�߰� | |||
| �n �h �� �� |
�o �� �I �� |
�z�q | ��(�d��+1) | 1/2 | ������ | 1919�̫��ށC���z�q1955���� |
| �����q | ��(�d��0) | 1/2 | ������ | 1932������ | ||
| �����_���q | ���O | 1/2 | ������ | 1949-59�߳��,���ް�� | ||
| �V�O�}���q | ���{ | 1/2 | ������ | |||
| ���O | 1/2 | ������ | ||||
| ���| | 1/2 | ������ | ||||
| �O�U�C���q | ���O | 1/2 | ������ | |||
| ���| | 1/2 | ������ | ||||
| �f���^���q | ���{�{ | 3/2 | ������ | |||
| ���{ | 3/2 | ������ | ||||
| ���O | 3/2 | ������ | ||||
| ���| | 3/2 | ������ | ||||
| �I���K���q | ���| | 3/2 | ������ | |||
| �� �� �q �� �� �\ �� �� |
�p�C���Ԏq | ���O | 0 | �����q���|�C 1940��ϰ(��) | ||
| ���{ | 0 | 1936���ް�� | ||||
| �j���Ԏq | �j�{ | 0 | ||||
| �C�[�^���Ԏq | ���O | 0 | ||||
���n�h�����Ƃ́u�������q�v�̈Ӗ��B�d���́C�d�͂Ƃ͕ʂ̗͂̑��ݍ�p������B�Q�̊j�q�̈�������Ԏq���o���C�������z������Ƃ��������ߒ����p�ɂɋN���邽�߂ɁC�j�͂��d���͂ɔ�ׂċ����B���v�g���͌y���q�B�Q. �N�H�[�N(quark)�ƃ��v�g��(lepton)
��������g���������ɂ���āC�n�h����(Hadron)�̓t���[�o�[(����)�ƌĂ��ʎq���ŕ��ނ����U��ނ��N�H�[�N���q����Ȃ�C�n�h�����͂R�̃N�H�[�N����Ȃ��o���I��(baryon)�C�P�̃N�H�[�N�ƂP�̔��N�H�[�N����Ȃ郁�\��(���Ԏq)�ɕ��ނ����B�Ⴆ�Ηz�q�͂Q�̃A�b�v�N�H�[�N�ƂP�̃_�E���N�H�[�N����Ȃ�(uud)�C�����q�͂P�̃A�b�v�N�H�[�N�ƂQ�̃_�E���N�H�[�N����Ȃ�(udd)�B���̑��̃n�h�����ƃN�H�[�N�̑g�ݍ��킹�͏�\���Q�Ƃ̂��ƁB
���\�ɃN�H�[�N�̓d�ׂ��������C�n�h�����̓d�ׂ͓d�C�f�ʂ̐����{��0�ɂȂ��Ă���B�N�H�[�N�͒P�Ƃł̑��݂͊m�F����ĂȂ��B
���v�g���̓N�H�[�N�Ɠ������U��ނ��邪�C�����\�����������N�H�[�N�Ɠ�����{���q�ƍl�����Ă���B
| �N�H�[�N | |||
| �N�H�[�N | �d��(��) | �X�s�� | ���� |
| �� (�A�b�v) | 2/3 | 1/2 | 1 |
| �� (�_�E��) | -1/3 | 1/2 | 1 |
| �� (�`���[��) | 2/3 | 1/2 | 2 |
| �� (�X�g�����W) | -1/3 | 1/2 | 2 |
| �� (�g�b�v) | 2/3 | 1/2 | 3 |
| �� (�{�g��) | -1/3 | 1/2 | 3 |
�� �N�H�[�N�̌ꌹ�́C�W���C�X�̝R��Ɂu���A�C�������h�̔��������܃C�]���f���A���P�剤�ɉł��Ƃ��C����g�~�ꂩ��D�o���悤�Ƃ���Ƃ��s�v�c�Ȓ�������āC�N�H�[�N�C�N�H�[�N�C�N�H�[�N�ƂR������Ƃ��������v�B�R�̕s�v�c�ȗ��q(��ꐢ��N�H�[�N)�̖��O�ɂ́C���̕s�v�c�Ȓ��̖����������������Ƃ��ăN�H�[�N�Ƃ����Ƃ����B
21�d�q�ƌ�
��132 ���ꒆ�̓d�q�̉^��
�^�ŐÎ~���Ă����d�q���d��V[V�n�ʼn�������C���_�n��ʂ��āC�������xB[Wb/m2]��z�����ɕ��s�ň�l�Ȏ�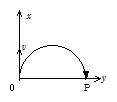 ��֓��˂����B�d�q�̎��ʂ�m[kg�n�C�d�ׂ��|e[C�n�Ƃ��āC�ȉ��̖₢�ɓ�����B
��֓��˂����B�d�q�̎��ʂ�m[kg�n�C�d�ׂ��|e[C�n�Ƃ��āC�ȉ��̖₢�ɓ�����B
(1) ���ꒆ�ł̓d�q�̑���v �����߂�B
(2) �}�̂悤�ɁC�d�q��x �����ɓ��˂����̂��C���ꒆ�ʼn~�O����`��y ����̓_�o�ɒB�����B���̖₢�ɓ�����B
(a) ���ʂɑ��鎥��̌����������B
(b) �����n�o�����߂�B
(3) �d�q�����_�n��ʉ߂���Ƃ������30߂̊p���Ȃ������֓��˂����ꍇ�ɂ��āC���̖₢�ɓ�����B
�@ (a) �d�q�͂ǂ̂悤�ȉ^�������邩�B
(b) �d�q�����_���o�Ă���C�ӂ�����z ����̂���_�p��ʂ�܂ł̎��ԂƋ����n�p���� �߂�B
��133�d���ꒆ�̗z�q�̉^��
�}�̂悤�ȑ��u���^�ɒu����Ă���B���W���Ƃ��̌��_O��}�̂悤�ɂƂ�Bz���̐������͎��ʂɐ����ɗ�����\����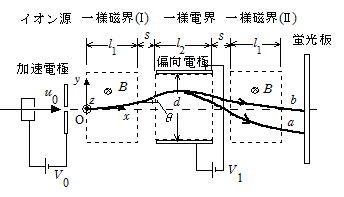 �ł���B�C�I�����ō��ꂽ�����x0 �̗z�q(�d�ׁ{e�C����m)�́C�d��V0�̂������Ă�������d�ɂɂ��x ��������������B�z�q�͈�l���E(����)(�T)�C��l�d�E(�d��)�C��l���E(�U)�ɂ��Ȃ����C�u���ɂ��ϑ������B�}���̋Ȑ�a�͗z�q�̋O���̈������������̂ł���B��l���E�͐}���̔j���ň͂܂ꂽ2�̗̈�ɂ������C������̗̈�ł��Cx �������̒�����l1�C���E�̕�����z���̕������C���E�̋����͎������xB�ł���B��l�d�E�́Cx���ɕ��s�ɒu���ꂽ����l2�C�Ԋud �̕Ό��d�ɂɓd��V1�������邱�Ƃɂ��}���̓_���ň͂܂ꂽ�̈�ɍ����B�d�ɂ̋ɐ��͏㑤�����ł���B��l���E�ƈ�l�d�E�̗̈�͋���s�����u�Ă��Ă���B�z�q�́|d/2��y���{d/2�͈݂̔͂̂��^��������̂Ƃ��C�܂��z�q�ɂ͂��炭�d�͂̉e���͖����ł�����̂Ƃ���B�ȉ��̖₢�ɓ�����B
�ł���B�C�I�����ō��ꂽ�����x0 �̗z�q(�d�ׁ{e�C����m)�́C�d��V0�̂������Ă�������d�ɂɂ��x ��������������B�z�q�͈�l���E(����)(�T)�C��l�d�E(�d��)�C��l���E(�U)�ɂ��Ȃ����C�u���ɂ��ϑ������B�}���̋Ȑ�a�͗z�q�̋O���̈������������̂ł���B��l���E�͐}���̔j���ň͂܂ꂽ2�̗̈�ɂ������C������̗̈�ł��Cx �������̒�����l1�C���E�̕�����z���̕������C���E�̋����͎������xB�ł���B��l�d�E�́Cx���ɕ��s�ɒu���ꂽ����l2�C�Ԋud �̕Ό��d�ɂɓd��V1�������邱�Ƃɂ��}���̓_���ň͂܂ꂽ�̈�ɍ����B�d�ɂ̋ɐ��͏㑤�����ł���B��l���E�ƈ�l�d�E�̗̈�͋���s�����u�Ă��Ă���B�z�q�́|d/2��y���{d/2�͈݂̔͂̂��^��������̂Ƃ��C�܂��z�q�ɂ͂��炭�d�͂̉e���͖����ł�����̂Ƃ���B�ȉ��̖₢�ɓ�����B
(1) �����d�ɂ��o���Ƃ��̗z�q�̑���u0��e�Cm�CV0��p���ĕ\���B
(2) ��l���E(�T)���o���ʒu(x��l1)�ŗz�q�̑��x��x ���ƂȂ��p�x�����Ƃ��āCsin����e�Cm�Cu0�Cl1�CB��p���ĕ\���B
(3) ��l�d�E�̒����i�ʒu(x��l1�{s�{l2/2)�ł̗z�q�̑��x��x����wx��y ����wy��e�Cm�Cu0�C���Cl2�Cd�CV1��p���ĕ\���B
22�g�����Ɨ��q��
��134 ���d����
�i�g���E�����A�ɂƂ�����d�q�ǂ�p���C�}1�̉�H�������d���ʂ̎������s�����B�ȉ��̖₢�ɓ�����B�������C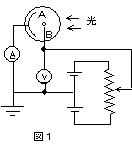 �����xc��3.0�~108m/s�C�d�C�f��e��1.6�~10-19C�Ƃ���B
�����xc��3.0�~108m/s�C�d�C�f��e��1.6�~10-19C�Ƃ���B
(1) �g��3.0�~10-7m�̎��O�������ĂȂ���CAB�ԂɈ��d�����������Ƃ���C��H��1.6�~10-6�`�̓d�������ꂽ�B
�@�@�A��A����z��B�ɒB����d�q�̐��͖��b�����B
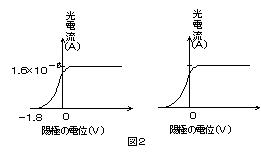
(2) AB�Ԃ̓d����ς��Ȃ�����d���𑪒肷��ƁC�}2�̂悤�ȃO���t�iI�|V �Ȑ��j������ꂽ�B�A�ɂ����яo�����d�q�̍ő�^���G�l���M�[[eV]�͂����炩�B
(3) ���̔g����ς����Ɍ��̋��x����������ƁC�}2��I�|V �Ȑ��͂ǂ��ς�邩�B�������̐}�ɏ������߁B
�@�@�i�Ȑ��̕ω��͒萫�I�ł悢�B�j
(4) ���Ă���̔g����ς��Ȃ���(2)�Ɠ��l�̎������s���C�����̌��ʂ���}3���쐬�����B�}���C�i�g���E���̎d����[eV]�ƃv�����N�萔[J�s]�����߂�B
(5) �w���E����l�I�����[�U�[�̌�(�g��6.3�~10�|7m)�����̌��d�ǂɂ��Ă�Ƃ��C���d���ʂ͋N���邩�B
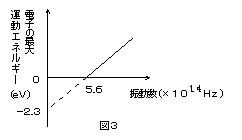
��135 �d�q�g�̉��
�^�ŋ�������2000߂b���x�ɉ��M����ƁC���������d�q�̕��o���N����(�����M�d�q���o�Ƃ���)�B���̓d�q��d��ʼn���������C�����ɏƎ˂�����B�d�q�͗��q�I�����ƂƂ��ɔg���Ƃ��Ă̐����������߁C�������̌��q�ɂ���ĉ�܂��N�����B���̌��ۂɂ��Ĉȉ��̖₢�ɓ�����B�K�v�ɉ����C���ɗ^���鐔�l��p����B�d�q�̎���m��9.1�~10�|31[Kg]�C�d�C�f��e��1.6�~10�|19[C]�C�v�����N�萔h��6.6�~10�|34[J�s]
(1) �d�q���g���Ƃ��ĐU�镑���Ƃ��̔g(�d�q�g)�̔g�����͓d�q�̉^����p �ƃv�����N�萔h�ŕ\�����B���̊W����������͂�蓱�����Ƃɂ���B
�����C���ʁC���Ԃ̎��������ꂼ��L�CM�CT�Ƃ������Cp�Ch �̎�����\���B
(2) ������ pX hY�Ƃ�����X��Y�̒l���߂�(���͖������̌W���ł���)�B���ʂo����ߒ����L�����ƁB���͂��̉�͂���͒�܂�Ȃ����C�g�����Ɨ��q���Ɋւ��鑽���̎�������������1�Ƃ��Ă悢���Ƃ������Ă���B
(3) �M�d�q�̏����x��0[m/s]�Ƃ��āC�d�ʍ�V[V]�ʼn������ꂽ�d�q�̉^����p ��m�Ce�CV��p���ĕ\���B����4.0�~10�|11[m]�̓d�q�g�邽�߂ɂ́C���{���g�ʼn�������悢���B�L������2���œ�����B
�@�����ɓ��˂����d�q�g�͌������i���邪�C�������̌��q�ɂ���ĎU������B�U�����ꂽ�d�q�g�͌��q�𒆐S�Ƃ��Ă��낢��ȕ����ɐi��ł����B1�̕��ʏ�ɂ��鑽���̌��q����U�����ꂽ�d�q�g�ɒ��ڂ���ƁC�����݂͌��Ɋ����āC���̕��ʔg�����ʂƍl�����Ƃ��ɓ��˔g�̕����ɑ��Ĕ��˂̖@�����������ŋ��ߍ����B���̂��Ƃ͌��q���܂ޕ��ʂ����˔g�ɑ��ċ��ʂ̂悤�ɍ�p���邱�Ƃ������Ă���B���̗l�ȕ��ʂ������ʂ܂��͊i�q�ʂƂ������C�������ɂ͒��ڂ��������ʂƕ��s�Ȃ�������̌����ʂ�����C���̂��ꂼ��̌����ʂ͓��˔g�������ɔ��˂����邱�ƂɂȂ�B�אڂ���2�̕��s�Ȍ����ʂ��甽�˂��ꂽ�d�q�g�݂͌��Ɋ����ċ��ߍ������ƂɂȂ�B���̂悤�ɁC�d�q�g�̓��˕����ƌ����̌��q�̕��ѕ��Ɋ֘A���Ē�܂����ȕ����ɎU�����ꂽ�d�q�g���i�ނ��Ƃ��C�����ɂ��d�q����܂ƌĂ��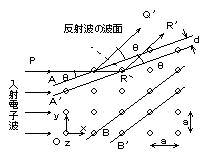 ����B
����B
(4) �}�͌����̌��q�ʒu�Ɠd�q�g�̓��˕���(X������)��\���Ă���B�����xy�ʏ�̌��q�ʒu�ł���Cz�������ɂ����q�͊Ԋua�Ŏ����I�ɕ���ł���Ƃ���BA�͎��ʂɐ����Ȍ����ʂł���C����ɕ��s�ŗאڂ��������ʂ�A'�ƕ\���B2�̖ʂ͋���d �����u�Ă��Ă���B���͌�����A�Ɠ��˕�����xy�ʓ��łȂ��p�ł���BP����Q�Ɍ������Đi�s���Ă���d�q�g�͌�����A��QQ'�����Ɍ�����A'�ł�RR' �����ɔ��˂����B�_���͔��˔g�̔g�ʂ�\���Ă���BQQ'
��RR' �����ɐi��2�̓d�q�g�ɐ����Ă���s�H����d ������p���ĕ\���B�܂��C���̕����œd�q�g��܂̋N��������������B
(5) �i�q�萔��a��2.0�~10�|10[m]�̌�����(3)�œ����d�q�g���Ǝ˂������Ƃ���C������A�Ƃ���ɕ��s�Ȍ����ʂɂ���ēd�q����܂��ϑ����ꂽ�B������A��A' �Ŕ��˂����d�q�g�̊Ԃɐ������s�H���͔g���̉��{���B
(6) ���̂Ƃ��C�����ʂa�Ƃ���ɕ��s�Ȍ����ʂɂ���Ă��d�q����܂��ϑ������B
�@�@�@(�@) �d�q����܂��ϑ������������q�ׂ�B
�@�@�@(�A) �����ʂa�Ƃ���ɕ��s�ŗאڂ��錋���ʂŔ��˂���2�̓d�q�g�ɐ����Ă���s�H���͔g���̉��{���B
��136 �w���C�d�q���̉��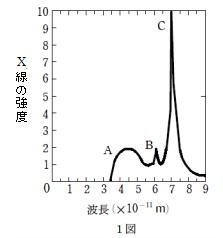
X ���́C�^��Ǔ��ō����d���ʼn������ꂽ�d�q�������ɏՓ˂���Ƃ��ɔ�������B����d���̉��Ŕ������� X ���̋��x�Ɣg���̊W (�X�y�N�g��)
�ׂ��Ƃ���C1 �}�̂悤�Ȍ��ʂ�����ꂽ�B���̃X�y�N�g���́C�ŒZ�̔g�����������g�����A���I�Ɋ܂܂��A�� X ���̕��� (1 �}�� A)
�ƁC����̔g���ɉs�������ŗL X ���̕��� (1 �}�� B �� C) �Ƃ���\������Ă���B��҂͋����̕����ɌŗL�̂��̂ł��邱�Ƃ��m���Ă���B�v�����N�萔h��6.6�~10 -34 J�s�C�d�q�̓d�ׂ̑傫��e��1.6�~10 -19C�C����c��3.0�~108 m/s�C�d�q�̎���m��9.1�~10 -31 kg �Ƃ��āC�ȉ��̖₢�ɓ�����B�L�������� 2 ���Ƃ���B
(1) �����Ŏg�p�����d���̑傫�������߂�B
(2) �A���I�ȃX�y�N�g�����������錴�����������B
�@��L��X������ŗLX���� C �݂̂����o���C������C2�}�̂悤�Ɍ��q��ʂ̊Ԋu�� d �ł��錋���ɑ��āC���q��ʂ����̊p�x�œ��˂����āC�� ��ω������Ȃ��甽�� X ���̋��x I �𑪒肵���B
(3) �� �� 0߂��瑝�������Ƃ��CI �� 4��ڂ̋ɑ���������p�x������30߂ł������B������ d �����߂�B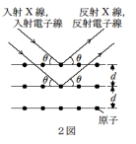
�@���ɁC�O��Ɠ���̌����ɑ��āCX ���̂����ɁC�d�� V �ʼn������ꂽ�d�q���� 2 �}�̂悤�ɓ��˂����āCV ��ω������Ȃ�����˓d�q���̋��x�ɑ��锽�˓d�q���̋��x�̊��� R �𑪒肵���B
(4) �����d�� V �Ɠd�q���̔g����e �̊W���������B
(5) �� ��30߂ɌŒ肵���Ƃ��C1 kV��V��2 kV �͈̔͂ɂ�����R ���ɑ�͉��邩�B
23���q�\��
��137�{�[�A���f��
�{�[�A�̌��q���f���ɂ��Ď��̖₢�ɓ�����B
(1) �ÓT�����w�Ō��q���������ɂ͖����_������B�ǂ̂悤�Ȗ��������邩�B�Q������������B
���f���q�̊j(�z�q)�͐Î~���Ă�����̂Ƃ��C�d�q(����m�C�d�ׁ|e)�͔��ar �̓����~�^�������Ă���Ɖ��肷��B
(2) �Ód�C�Ɋւ���N�[�����̖@���̒萔��k �Ƃ��āC�d�q�̑���v ��m�Ce�Ck�Cr ��p���ĕ\���B
(3) �d�q�̔g�������l����ƁC�d�q�̋O���̒����͓d�q�̕����g�Ƃ��Ă̔g���̐����{�łȂ���Ȃ�Ȃ��B�d�C�̋O�����a r �𐳂̐��� n�C�v�����N�萔h�Cm�Ce�Ck ��p���ĕ\���B
(4) ���f���q�̃G�l���M�[��n�Ch�Cm�Ce�Ck ��p���ĕ\���B
24���q�j
��138���ː�����
| �o�ߎ���[h] | ���˔\�̋���[Bq] |
| 0 | 300 |
| 2 | 225 |
| 4 | 172 |
| 6 | 131 |
| 8 | 99 |
| 10 | 75 |
| 12 | 57 |
| 14 | 43 |
| 16 | 32 |
1896�N�C�x�N�����̓E�������畨�����悭���߂��ʐ^�������������鉽�������o����Ă��邱�Ƃ��������B���̕��o����Ă�����̂���ː��Ƃ����C���ː����o����������˔\�Ƃ����B���q�j�́C[�A]
��[�C] �Ƃ���ł��Ă���C(�A)�̐��͌��q�ԍ��ɓ������C (�A)��(�C)�̐������������̂�[�E]��\���Ă���B���q�j�ɂ͌��q�ԍ��������ł�(�E)���قȂ���̂����肱��ʑ̂Ƃ����B���ʑ̂ɂ͈���Ȃ��̂ƕs����Ȃ��̂�����B�s����Ȍ��q�j�ɂ́C���ː�����o���ĕʂ̌��q�j�ɕς����̂�C�قڔ�����(�E)��������2�̌��q�j�Ɋj������̂�����B���R�E�ɂ̓w���E���̌��q�j����o����[�G]����C�d�q����o����[�I]
����C����уG�l���M�[�̑傫�����q����o����[�J] ������B���������āC(�G)����ł́C���錴�q�j�̌��q�ԍ���[�L] �����ω����C(�E)��[�N]�����ω�����B�܂��C(�I)����ł͌��q�ԍ���[�P]�����ω����C(�E)�͕ς��Ȃ��B(�J)����ł͕���̑O��Ō��q�ԍ���(�E)���ω����Ȃ��B
���ː�����ł́C���錴�q�j�̐��������ɂȂ鎞�Ԃ����Ƃ����C���q�j�̎�ނɂ���Č��܂��Ă���B
�܂��C���ː����q�j�̒P�ʎ��Ԃ�����ɕ��鐔�́C���ː����q�j�̐�N(��)�ɔ�Ⴗ��B���˔\�̋����́C�P�ʎ��ԓ�����̕���(����)�Ō��߂��C���b1�̊����ŕ�����˔\�̋�����1Bq(�x�N����)�Ƃ����B
���܁C1��ނ̓��ʑ̂�������ɔ����h�z����Ă������(�����Ƃ���)������B���̕��˔\�̋����C���ʑ̂̐��C����є��������s���ł��邪�C�����铯�ʑ̂ł��邱�Ƃ��������Ă���B���̐����̕��˔\�̋�������є������𑪒肷������������Ȃ����B
(1) [�A] ����[�P] �ɓK���Ȍ��C�L���܂��͐���������B
(2) ���ː����o���p���ē��ʑ̂̕��˔\�̋�����2���Ԃ����ɂ��̒l���͂��߂̖�ɂȂ�܂ő�����s�����B���肳�ꂽ���˔\�̋����͕\1�̂悤�ɂȂ����B���˔\�̋������c���ɁC���Ԃ������ɂƂ��đ��茋�ʂ�}��
� ���p���ċL�����C���˔\�̌����������Ȑ���`���B
(3) ���˔\�̋������͂��߂�![]() �����
�����![]() �ɂȂ�܂ł̎��Ԃ͂����炩�B(2)�ŕ`�����Ȑ�����L������2���܂ŋ��߂�B
�ɂȂ�܂ł̎��Ԃ͂����炩�B(2)�ŕ`�����Ȑ�����L������2���܂ŋ��߂�B
(4) ���ʑ̂̔�������T(h)�C�͂��߂̕��˔\�̋�����A0(Bq)�Ƃ���ƁCt(h)��̕��˔\�̋���A(Bq)�͂ǂ̂悤�ɕ\����邩�B
(5) ���˔\�̋����͂��̂Ƃ��ɑ��݂��铯�ʑ̂̐�N(��)�ɔ�Ⴗ�邱�Ƃ��킩���Ă���B�����J�n���̓��ʑ̂̐���N0(��)�Ƃ��āCN��N0�͂ǂ̂悤�ȊW�ɂ��邩�B(4)�̌��ʂ�p���Ď����B
25�j����j�Z��
��139�j����
�E������g���E���Ȃǂ̌��q�j�́C���R�ɕ��ː����o����[�A] ��[�C] ���قȂ錴�q�j�ɕς���Ă����B���̂悤�Ɏ��R�ɕ��ː����o�����f��[�E]�Ƃ����C���̂悤�Ȑ�����[�G]
�Ƃ����B(�E)�����ː����o���đ��̌��q�j�ɕϊ����邱�Ƃ�[�I]�Ƃ����C���̂Ƃ��ɕ��o�������ː��ɂ́C�����������Ȃǂ�����B������[�J]�̗���ł���C������[�L]�̗���ł���B
�V�R�E�����̑啔���́C�j������N�����Ȃ��E����![]() �ł���C���̌��q�j�́C�z�q[�N]�C�����q[�P]����Ȃ�B�E����
�ł���C���̌��q�j�́C�z�q[�N]�C�����q[�P]����Ȃ�B�E����![]() ���C������������1���o����C(�A)��[�R] �C(�C)��[�T] �̌��f�ɂȂ�B�j������N�����E����
���C������������1���o����C(�A)��[�R] �C(�C)��[�T] �̌��f�ɂȂ�B�j������N�����E����![]() �̑��ݔ�́C�V�R�E�����̂킸��0.7���ɂ����߂��Ȃ��B���̂悤�ȃE����
�̑��ݔ�́C�V�R�E�����̂킸��0.7���ɂ����߂��Ȃ��B���̂悤�ȃE����![]() ��Z�k��������āC���q�͔��d�̔R���Ƃ��Ďg�p���Ă���B
��Z�k��������āC���q�͔��d�̔R���Ƃ��Ďg�p���Ă���B![]() ��
��![]() �̂悤��(�A)�������ŁC(�C)�̈قȂ錳�f�̂��Ƃ�[�V] �Ƃ����B�E����
�̂悤��(�A)�������ŁC(�C)�̈قȂ錳�f�̂��Ƃ�[�V] �Ƃ����B�E����![]() �ɒ����q��������ƁC�j������N�����ĕ����̒����q����o���C�Q�̌��q�j�ɕ���ꍇ������B
�ɒ����q��������ƁC�j������N�����ĕ����̒����q����o���C�Q�̌��q�j�ɕ���ꍇ������B
���̈��Ƃ��āC ![]() �{
�{![]() ��
��![]() �{
�{![]() �{3
�{3![]() ������@
������@
�̂悤�Ȋj��������������B���̂Ƃ��C�����O�̃E����![]() �ƒ����q
�ƒ����q![]() �̎��ʂ̘a�́C�����̃X�g�����`�E��
�̎��ʂ̘a�́C�����̃X�g�����`�E��![]() �C�L�Z�m��
�C�L�Z�m��![]() ,�����q
,�����q![]() �̎��ʂ̘a�����傫������̎��ʂ̍���[�X] �Ƃ����B�j���������ł́C(�X)�ɑ�������G�l���M�[�����o�����B
�̎��ʂ̘a�����傫������̎��ʂ̍���[�X] �Ƃ����B�j���������ł́C(�X)�ɑ�������G�l���M�[�����o�����B
(1) ���͒���[�A]�`[�X]�ɍł����Ă͂܂���͉̂����B
(2) �����q![]() �C����уX�g�����`�E��
�C����уX�g�����`�E��![]() �C�L�Z�m��
�C�L�Z�m��![]() �C�E����
�C�E����![]() �̊e���q�j1�̎��ʂ��C���ꂼ��1.67�~10�|27Kg�C154.28�~10�|27Kg�C
�̊e���q�j1�̎��ʂ��C���ꂼ��1.67�~10�|27Kg�C154.28�~10�|27Kg�C
232.34�~10�|27Kg�C390.29�~10�|27Kg�Ƃ����Ƃ��C�@���̊j���������ɂ����1�̃E�������q�j������o�����G�l���M�[�͂����炩�B�^�̌��̑�����3.0�~108m/s�Ƃ���B
��140�j����
| n | 1.00866u |
| 10.01019u | |
| 7.01435u | |
| 4.00150u |
�����qn�C����ь��q�j ![]() �C
�C![]() �C
�C![]() �̎��ʂ́C���q���ʒP�ʁi�L��u�j���g���ƁC�\�̂悤�Ȓl�����B�܂��C���ʂPu�ɑ������鎿�ʃG�l���M�[��9.31�~102MeV�ł���B
�̎��ʂ́C���q���ʒP�ʁi�L��u�j���g���ƁC�\�̂悤�Ȓl�����B�܂��C���ʂPu�ɑ������鎿�ʃG�l���M�[��9.31�~102MeV�ł���B
�@���āC�������قƂ��0 �̒����qn ���C�Î~���Ă��錴�q�j![]() �ɏՓ˂����C���̂悤�Ȍ��q�j�������N��������B
�ɏՓ˂����C���̂悤�Ȍ��q�j�������N��������B
�@�@n�{ ![]() ��
�� ![]() �{
�{![]() ������(A)
������(A)
����ɂ��Ď��̖�ɓ�����B�������C���˒����q�̉^���G�l���M�[�͖������Ă悢�B�܂��C���l�͗L�������Q���܂ŋ��߂�B
(1) ����(A)�ŕ��o�����G�l���M�[�̒l��MeV�P�ʂœ�����B
(2) ���o�����G�l���M�[�͂��ׂĉ^���G�l���M�[�ɂȂ�Ƃ��āC���q�j![]() �����
�����![]() �̉^���G�l���M�[�̒l�����ꂼ�ꋁ�߁CMeV�P�ʂœ�����B
�̉^���G�l���M�[�̒l�����ꂼ�ꋁ�߁CMeV�P�ʂœ�����B
(3) ����(A)���C��l�Ȏ��E�̑��݂���^�ŋN�������Ƃ���B�܂��C���E�̕����ƁC���q�j![]() �̏����x�̕����Ƃ݂͌��ɐ����ł���Ƃ���B
�̏����x�̕����Ƃ݂͌��ɐ����ł���Ƃ���B
���̂Ƃ��C���q�j![]() �����
�����![]() �́C���ꂼ��C���̔��a�����~�O������^������B
�́C���ꂼ��C���̔��a�����~�O������^������B
���q�j![]() �̋O�����a��a�C���q�j
�̋O�����a��a�C���q�j![]() �̋O�����a��b�Ƃ��Cb/a�����߂�B
�̋O�����a��b�Ƃ��Cb/a�����߂�B
�@���ɁC�����̋O���̐}�������B���̍ہC���E�̕����͎��ʂɐ����ŁC���ʂ̗�����\�Ɍ��������̂Ƃ���B�Ȃ��C���O���̏o���_���~��ŁC�����Đi�s�̌�������Ŗ�������B�܂��C���ꂼ��̋O���ɑ��錴�q�j�̋L�����L������B�������C���q�j�͂��ׂāC�d�q���Ă��Ȃ��Ƃ���B
��141�j�Z������
�d���f�̌��q�j![]() �ƎO�d���f�̌��q�j
�ƎO�d���f�̌��q�j![]() ���10KeV�܂��͂���ȏ�̉^���G�l���M�[�ŏՓ˂����C�j�Z���������N�����C���̊j�����ŕ��o������j�G�l���M�[���G�l���M�[���Ƃ��ė��p���邱�Ƃ��l�����Ă���B�ȉ��̊j�Z�������Ɋւ���₢�ɓ�����B
[ ] ���ɂ͊Y������L�����邢�͗p�������B
���10KeV�܂��͂���ȏ�̉^���G�l���M�[�ŏՓ˂����C�j�Z���������N�����C���̊j�����ŕ��o������j�G�l���M�[���G�l���M�[���Ƃ��ė��p���邱�Ƃ��l�����Ă���B�ȉ��̊j�Z�������Ɋւ���₢�ɓ�����B
[ ] ���ɂ͊Y������L�����邢�͗p�������B
(1) ���̊j�Z���͎��̂悤�Ȋj�����ŕ\�����B
�@�@�@�@![]() �@�{
�@�{ ![]() �� [�A] �{
�� [�A] �{![]() (
( ![]() �͒����q�ł���)
�͒����q�ł���)
(2) ���̊j�����ɂ��C������̌��q�j�̎��ʂ̘a�́C�����O�̌��q�j�̎��ʂ̘a���C0.019u������������B���̌�����[�C] �Ƃ���B
�����ŁC1u��1.66�~10�|27Kg�ł���B
(3) �A�C���V���^�C����1905�N�ɔ��\����[�E] ���_�ɂ��ƁC���ʂƃG�l���M�[�͓����ł���C�G�l���M�[��E�C���ʂ�m�C�^�̌��̑�����c �Ƃ���Ƃ����̊Ԃɂ�[�G] �̊W�����藧�B
(4) �O��(2)�̎��ʂ̌���(��)�ɑ�������G�l���M�[���v�Z���C�kJ�l����сkeV�l�Ŏ����B�������C���̑�����c��3.00�~108(m/s)�ł���C
1eV ��1.60�~10�|19J�ł���B
�z�[�� ���j���[ �d�q�ƌ� �g�����Ɨ��q�� ���q�\�� ���q�j �j����j�Z�� �N�H�[�N