ホーム メニュー ![]() 静電界 コンデンサー 直流回路 磁界 電磁誘導 交流
静電界 コンデンサー 直流回路 磁界 電磁誘導 交流
【17】コンデンサー
17-1 コンデンサー(condenser)とは
2枚の金属極板を向かい合わせ、電位差を与えることにより、正負の電荷を蓄えることを目的に作られたものがコンデンサーである。一対の平行な金属板を極板とするものを平行板コンデンサーという。コンデンサーの種類を構造で分類すると、ライデン瓶、バリコン(可変コンデンサー)、マイカ(雲母)、パラフィンコンデンサー、電解コンデンサーなど。形状で分類すると平行板、球状、円筒状コンデンサーである。
極板間に入れられる誘電体(誘電分極の大きさを変えるために入れる)の種類によって、電解コンデンサー、空気コンデンサー、ペーパーコンデンサーなどがある。
コンデンサーの原理
① 金属板Aに正電荷を与える。電荷は一様に分布する。
② 帯電してない別の金属板Bを図の右側にもってくると、静電誘導 によって金属板Bの左側に、金属板Aの正電荷に引かれて負電荷が生じこれと等量の正電荷が右側に生じる。この結果金属板Aの右の方に電荷が集中する。
③ 金属板Bをアース(接地)すると、金属板BのAから遠い側にある正電荷が大地に逃げ、Bは負電荷だけになる。Bの左側の負電荷は金属板Aの正電荷に引かれていて移動できないためである。
④ 金属板A、B間に誘電体(不導体)を挿入すると誘電分極によって誘電体の右が正、左が負に帯電し、これによって金属板A、Bともに内側に電荷が集中する。この結果これらの電荷が強く引き合って、強い電場が作られる。これがコンデンサーの原理である。こうして蓄えられた電荷は、必要に応じて放電(例えばカメラのフラッシュ)、充電を繰り返し利用される。金属板の面積、間隔、挿入された誘電体の種類によって蓄えられる電荷の量が変わる。図の②、③、④ともに静電誘導、④では誘電分極が原因となっている。①~④の電荷の変化を箔検電器で考えたものが下段の図である。図から分かるように、箔検電器の金属板が上段の図の金属板Aの右方、箔が金属板Aの左方に対応する。電荷をより多く蓄えるためには箔の開きがより小さくなるようにする必要があることがわかる。
17-2 電気容量(electrostatic capacity)は何によって変わるか
真空中にある平行板コンデンサーの場合は
物質 比誘電率 空気 1.00059 水 ≒80 絶縁油 2~2.5 絶縁紙 1.2~3.5 雲母 5~8 ポリエチレン 2.2~3.3 チタン酸バリウム ≒5000
極板上の電荷Q と電位差V(17-1)
で与えられる。ここで、
S[m2]は極板の対向面積(極板が向かいあっている部分の有効面積)
d[m]:極板間距離
ε0[F/m]:真空の誘電率である。
極板間の物質の誘電率がε の場合、比誘電率(真空の誘電率との比)をεr=として、電気容量C は
(17-2)
である。比誘電率の例は右表(常温での値)。
Sが大きくなる、dが小さくなると静電誘導が起こりやすくなり(上図②の金属板A、Bの間隔が小さくなるほど箔の開きは小さくなりA、Bの内側に電荷が集中する)、またε が大きいほど誘電分極が起こりやすくなる(上図④)。
つまり、静電誘導、誘電分極が起こりやすいほど、極板の内側に電荷が集中することになり、Cが大きくなる。このCを静電容量または電気容量という。
電気容量C のコンデンサーの極板に電位差V をかけると、コンデンサーに蓄えられる電荷Qは、Vに比例し(左図)
Q=CV (17-3)
の関係がある。C はQ とV の間の比例定数で電気容量である。つまり同じ電位差をかけても電気容量C が大きいほど蓄えられる電荷が多いことになる。
コンデンサーに蓄えられる電荷Q を、バケツに入れられた水に置き換えて考えると(左下図)、電気容量Cはバケツの底面積、電源は十分水量を蓄えた貯水槽、極板間の電位差Vは水位に相当する。バケツに入れられた水量は、底面積×水位で決まる。貯水槽は十分水量があるためバケツに水を送り込んでも貯水槽の水位は変わらない。コンデンサーに電源を接続すると電位差が上昇し、電源の電位差と等しくなるまで電荷が送り込まれる。
電気容量Cの単位はF(ファラッド)=C/Vで、1[V]の電位差を与えたときに1[C]の電荷が蓄えられる電気容量を 1[F]ときめる。 μF=10-6F、pF=10-12Fとする。
ガウスの法則を使って電気容量を求める
(図①) 正電荷Qを金属板に与え、金属板の面積をS とすると電場E1は
E1=4πkQ/2S=2πkQ/S が図の上下に作られる。
(図②) 同様に負電荷-Qを金属板に与えると電場E2は
E2=4πkQ/2S=2πkQ/S が図の上下金属板の向く向きに作られる。
(図③) ①、②の金属板を接近させると、①、②の電場は金属板からの距離に関係しないから、+Qに帯電された金属板の上は①、②による電場が逆向きなので打ち消し合って0になり、同様に-Qに帯電された金属板の下の電場も0になる。
金属板間は①、②の電場が同じ向きだからE=E1+E2=4πkQ/S になる。極板間の誘電率をεとすると
k=だから、
電場と電位差の間の関係は E=V/d だから
よって=CV ∴ C=
コンデンサーの充放電
電池の起電力E、回路中の抵抗R、コンデンサーの電気容量C、電流I、時間をt、電荷をqとする。充電の場合、キルヒホッフ第2法則(18-7で学ぶ)から(17-4)
t=0でq=0だからこのときの電流I0はである。電荷の最大値はI=0 だから、q=Q=CE 、(17-2)を時間で微分し
(17-5)
電荷は q(t)=Q(1-) (17-6) である。 (右図グラフ)
放電の場合、キルヒホッフの法則から、
から
t=0でq=Qであることを使って上式を積分して
(17-7)
(17-3)を時間に関して微分して、 I (t)=(17-8) (右図グラフ)
① 直列接続
コンデンサーの直列接続とは、はじめにそれぞれのコンデンサーに電荷が与えられてない場合、それぞれの電荷は等しく、等電位面上に異種の電荷が共存している。電荷が等しいから、電気容量、電位差を右図のようにすると、
q=C1V1=C2V2で
電位差は電気容量に反比例分配される。つまり、
合成容量Cは V0=V1+V2=(17-9) である。
② 並列接続
並列接続は、それぞれの電位差が等しい。電荷はCに比例分配される。
(
)
合成容量Cは q0=q1+q2=(C1+C2)V0=CV0 ∴ C=C1+C2 (17-10) である。
コンデンサーの等価回路
極板間に導体、誘電体などが挿入されている場合は次のように置き換えをして考える
極板間隔 d のコンデンサーの極板間に厚さ l の導体を挿入した場合、導体内の電場が0 (等電位)だから、極板間隔がd-l であるコンデンサーと等価である。はじめの電気容量をC0とすると挿入後の電気容量はである。
極板間隔dのコンデンサーの極板間に厚さl の誘電体を挿入した場合、 極板間隔がd-l のコンデンサーと、比誘電率εrの誘電体が挿入され極板間が極板間隔がd-l のコンデンサーの直列接続された場合と等価である。
挿入後の電気容量はである。
極板間隔d、幅がLのコンデンサーの極板間のうち、横幅x だけ比誘電率εrの誘電体が挿入された場合、電気容量と
のコンデンサーの並列接続と等価である。
合成容量はである。
17-4 静電エネルギー(electrostatic energy)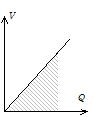
電気容量C[F]のコンデンサーにV[V]の電位差を与えると、電荷Qが与えられ、右図の斜線部分の大きさで決まる静電エネルギー (電荷dqを移動させる仕事dW=Vdqだから)
(17-11)
が蓄えられる。これはQ=CVの関係から[J] と書くこともできる。
電源は電位差V0を一定にして電荷Qを送り出すから、電源のした仕事はW=QVである。静電エネルギーはこの半分のである。つまり、コンデンサーは電源のした仕事の半分だけ受け取ることになるが、残りの半分は回路の電気抵抗による発熱(ジュール熱)に消費される。電源は電位差一定だが、コンデンサーの電位差は極板の電荷によって変化することに注意。
17-5 導体、誘電体中の電界、電位差
(1) 極板間に導体を挿入した場合コンデンサーの極板間の電位差がV、極板間隔 d の場合、電場は E0=V/dである。
コンデンサーの極板間に導体を挿入すると、導体中の自由電子の移動が外部の電界を打ち消すまで続くので、導体中の電場は0で、等電位になる。
電場、電位の分布は、①電源をつけたまま導体を挿入した場合と、②電源で充電後十分時間が経過した後に電源を外してから挿入した場合で異なる。
負極板の電位を 0 とし、正極板からの距離を左図のように x 、極板間隔を d、導体板の幅を l とした場合
① 起電力V0の電源をつけたまま導体を挿入する場合
極板間の電位差Vは電源電圧V0で充電すると、V=V0だが、導体部分の電位差は0である。電場Eは
E=これは、極板間隔がd-l になったことに相当し、電場は挿入する導体の幅によって変化する。
② 電源で充電後、十分時間が経過した後に電源を外してから導体を挿入する場合
極板の電荷は保存されるので、電場は導体を挿入する前と変わらずE=E0である(ガウスの法則で面積が一定の場合電荷と電場が比例することからも分かる)。したがって、極板間の電位差は
である。
この結果、導体板の幅 l を大きくするほど電位差が小さくなることが分かる。
左のE-x グラフのそれぞれの部分の面積がそれぞれの区間の電位差を示し、V-xグラフの傾きが電場の大きさを示す ( ([静電場]16-6式参照) )。
(2) 極板間に誘電体を挿入した場合
コンデンサーの極板間に比誘電率の誘電体を入れると、誘電体に誘電分極が起こり、誘電体に分極電荷が生じ、極板が作る電場E0と逆向きに電界E' ができるが|E'|<|E0|なので誘電体中にはE0と同じ向きにE0-E' の電界ができる。左図で極板に±Q0の電荷を与え電源を外した場合、誘電体表面には±qの分極電荷が生じる。極板間に誘電体がない場合の電場をE0(このときの電位差をV0、電気容量をC0とする)、誘電体が挿入されている場合の電場をE(このときの電位差をV、電気容量をC)、とすると、
の関係がある。これから
となるが、電場、電位の分布は、電源をつけたまま誘電体を挿入した場合と、電源で充電後十分時間が経過した後に電源を外してから挿入した場合で異なる。極板間隔をd、誘電体の幅をl、極板面積をS とする。
①電源をつけたまま誘電体を挿入する場合
極板間の電位差Vは電源電圧V0で充電すると、V=V0である。誘電体を挿入すると極板の電荷Qは、挿入前の電荷Q0より分極電荷qだけ増加する。真空部分の電場をE1、誘電体内の電場をE2、qが作る電場をE' とすると、
E2=E1-E' である。E2=E1/だから、E1/
=E1-E' ガウスの法則から
← 右辺は、qによって誘電分極の効果が代表されているから
でなくて
と扱える。
∴ 分極電荷は(
>1 だから |q|< |Q|)
誘電体が入らない場合の電荷Q0で表すと、だから、 (上記コンデンサーの等価回路参照のこと)
→ 誘電体の幅 l によってQが変化するので q も変化する。
∴→ d=0 で q=0 、d=l で
電場 E1、E2は、極板間の電位差の合計がV0だから
V0=E1(d-l)+E2l =E1(d-l)+(E1/) l
∴、
それぞれの区間の電位差は、E1、E2に距離を乗じた値である。
② 電源で充電後十分時間が経過した後に、電源を外してから誘電体を挿入する場合
極板の電荷は保存されるので、電場は導体を挿入する前と変わらずにE0=V0/l である。
誘電体内の電場はE0/だから、極板間の電位差は
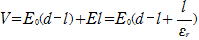
(l=dの場合、つまり極板間にすべて誘電体が挿入されるとV=)
誘電体の幅 l が大きくなると極板間の電位差は小さくなる。
分極電荷qが作る電場をE' とすると、E=E0-E' だから、①と同様にして
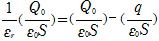
∴ 分極電荷(
>1だから |q|< |Q0| ) (上記①のq と比べてみよ)
極板の電荷がQ、電界の強さがEである場合、極板上の正負の電荷間の引力の大きさFは次のようにして求める。
① 極板間隔dの平行板コンデンサーに電源を接続して正負の電荷Qを与え、その後電源を外し、極板間隔をd+⊿dに変化させる。
この変化による静電エネルギー変化量⊿Uは、間隔を変えるために加えた外力(静電気力と等しい)F のなす仕事⊿W=F⊿dと等しい。
また、Q=CV=ε0SEだから
(17-11) である。
② コンデンサーに電源をつけたまま極板間隔を d から d+⊿d にゆっくり変化させる。⊿d>0 とする。
この場合,電位差V が一定で電気容量が小さくなるから静電エネルギーの変化量は
電源のする仕事WCは,コンデンサーの電荷が減るから負でその大きさは
つまり WC=2⊿U
外力がする仕事 WF,WC ,⊿U の間には ⊿ U= WF+WC の関係があるので,極板間隔をゆっくり変化させるための外力F がする仕事は正( F と 移動方向が同じ)で
∴
大きさの比は⊿dの正負に関係なく, |⊿ U|: |WF|:|WC|=1:1:2である。
(注) 極板をゆっくり移動しない場合,回路にジュール熱Qが発生する。その場合,⊿ U= WF+WC-Q とすればよい。
17-7 電荷保存
コンデンサーに与えられた電荷は、接続を変化させ電荷を移動させても電荷は保存される。
例1 下図のように電気容量がそれぞれC1,C2のコンデンサーに電荷q1、q2を与えておく。
電位差V '、q1'、q2 'は電荷保存から
接続1の場合
接続2の場合
接続3の場合(接続した電池の電位差をV0、C1、C2それぞれの電位差をV1、V2とする)
V0=V1+V2、q1'=C1V1、q2'=C2V2、-q1+q2=-q1'+q2' (電荷保存)から
例2 (電位を使って電荷を求める方法)
下図のように電気容量がそれぞれ1.0,2.0,3.0μFのコンデンサー(はじめすべて電荷は0とする)と,それぞれの起電力が 6.0,9.0V の電池を接続する。それぞれのコンデンサーのb点側の電荷を求めよ。
図のb点の電位をV [V],a点の電位を 0 とする。
1.0,2.0,3.0μFそれぞれの電位差は,V -6.0,V -9.0,V -0である。b点に接する電荷の和は 0 (はじめ電荷が 0 のため)だから,
1.0×(V -6.0)+2.0×(V -9.0)+3.0×V= 0 ∴ V= 4.0[V]
それぞれのコンデンサーのb点側の電荷は
1.0μF ・・・・・ (1.0×10-6)×(V -6.0)=-2.0×10-6[C]
2.0μF ・・・・・ (2.0×10-6)×(V -9.0)=-10×10-6[C]
3.0μF ・・・・・ (3.0×10-6)×V = 12×10-6[C]
16-1 静電誘導
問104 はく検電器がある。はくは最初閉じていたが、正に帯電した棒を上部の金属板に近づけると開いた(図①)。この状態で、はく検電器の金属板に指を触れて接地したところ、はくは閉じた(図②)。
続いて、指を金属板から離し(図③)、次に棒を遠ざけた(図④)。 図③、図④のはく検電器の金属板の電荷の符号、はくの開きと電荷の符号を書け。
16-4 電界 16-5 電位
問105 重力加速度g[m/s2]の一様な重力の働く真空中の鉛直面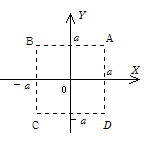 内に、図のように水平にX軸、鉛直上方にY軸をとる。長さの単位を[m]として、点A、B、CおよびDの座標はそれぞれ(a、a)、(-a、a)、(-a、-a)および(a、-a)である。真空中の誘電率はε0(C2/N・m2)、重力は鉛直下方に働くとする。
内に、図のように水平にX軸、鉛直上方にY軸をとる。長さの単位を[m]として、点A、B、CおよびDの座標はそれぞれ(a、a)、(-a、a)、(-a、-a)および(a、-a)である。真空中の誘電率はε0(C2/N・m2)、重力は鉛直下方に働くとする。
(1) 点AにQ[C](以下Q>0とする)の点電荷を固定すると、原点Oにおける電界の強さは何[V/m]か。
(2) (1)の状態で、さらに点Cに-Q[C]の点電荷を固定すると、原点Oにおける電界の強さは何[V/m]になるか。
(3) (2)の状態で、さらに点Bおよび点DにそれぞれQ[C]および-Q[C]の点電荷を固定すると、原点Oにおける電界の強さは何[V/m]になるか。
問106 長方形ABCDの2つの頂点A、Bにそれぞれ電荷q1=5.0×10-9[C]、q2=-4 .0×10-8[C]があり、長さAD=10[cm]、BD=20[cm]とする。
.0×10-8[C]があり、長さAD=10[cm]、BD=20[cm]とする。
また、q1=q2=1[C]、AB=1[m]のときq1、q2間のクーロン力が9×109[N]とする。
(1) A、B2点にある電荷q1、q2 間のクーロン引力Fの大きさはいくらか。
(2) 電荷q1によるD点における電界の強さE1の大きさはいくらか。
(3) 電荷q1、q2によるD点における電界の強さEの大きさ,および方向を求めよ。
(4) 2点D、C間の電位差Vはいくらか。ただし、電荷qからr の距離の点の電位は、kを比例定数としてで与えられ、
q=1[C]、r=1[m]でV=9×109[V]である。
16-7 電界中の仕事
問107
(1) 図で、+と- は電気量の絶対値q (c)が等しい正負の点電荷で、破線は一定の電位差(V[V])ごとに描かれた等電位線である。別の正電荷Q[C]をAからFまで実線に沿って矢印の向きに運ぶとき、外力のする仕事が、正で最大の区間はどこか。またその大きさはいくらか。
(2) (1)において、点電荷を上記のAからFまでの経路で電荷を移動させた場合と、Aから直接電荷をFまで移動させた場合、その大きさは等しいことがわかっている。その理由は、電界がどのような特徴を持っていることによるか。簡潔に説明せよ。
【17】コンデンサー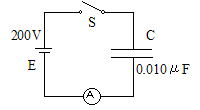
問108 図の回路でスイッチSを閉じる。はじめコンデンサーには電荷はなかったものとする。電池の起電力は200[V]、コンデンサーの電気容量Cは0.010[μF]である。
(1) Sを閉じたとき電流計Aには、どちら向きに電流が流れるか。
(2) Sを閉じてから充電が終わるまでに、電流計Aを流れる電気量(電荷)は何(C)か。
次にSを開き、コンデンサーCの極板の間隔を半分にする。
(3) Cの極板間の電圧は何[V]か。
この状態から再びSを閉じる。
(4) さらに電流計を流れる電気量(電荷)はどちら向きで、何(C)か。
問109 2枚の同じ形の導体板を極板とした平行板コンデンサーを考える。このコンデンサーの両極板に起電力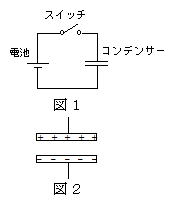 Vの電池とスイッチを図1のように接続した。
Vの電池とスイッチを図1のように接続した。
両極板間に何も入れないでスイッチを閉じたところ、コンデンサーの極板の電荷は図2のように分布した。
(1) スイッチを閉じたまま、極板間に比誘電率εrの誘電体を入れた。極板と誘電体上の電荷は図2と比べてどのようになるか。電荷の分布を描け。
(2) その後スイッチを開いてから、誘電体を抜いた。このとき、極板間の電位差はいくらになるか。
(3) 問2で、誘電体を抜いたあとのコンデンサーの静電エネルギーU2と、抜く前のコンデンサーの静電エネルギーU1との比U2/U1はいくらか。
ホーム メニュー 静電界 コンデンサー 直流回路 磁界 電磁誘導 交流