�z�[�� ���j���[ ![]() �Ód�E �R���f���T�[ ������H ���E �d���U�� ��
�Ód�E �R���f���T�[ ������H ���E �d���U�� ��
�y�P�X�z�d���Ǝ��E
�P�X�|�P ���E(magnetic field)
���Η��[��Fe�CNi �Ȃǂ��������镔�������ɂƂ����C���̋���������(���C��)�Ƃ����B
���C�Ɋւ���N�[�����̖@�� �Ód�C�Ɋւ���˂��ꔉ�ő��肵���Ɠ��l�ɂ��Ĉȉ��̖@���������B(1785�N)
(�x�N�g���\�������
) (19-1) �����̋t����͖��L���́C�Ód��̃N�[�����͂Ɠ���

�@�@���F������(N/A2)�Cm�Cm'�F����(Wb���E�G�[�o�[)
�����ɐ^�̓�������0���ł���B
���EH���E�̋���H�́C�P�ʎ��ׂ�u�����Ƃ��C1N�̗͂��鋭���ƒ�߂�B
���ׂ�m(Wb)�C��F(N)�Ƃ����
(N/Wb) (19-2)
����m���狗��r �̈ʒu�ł̎��E�̋�����(19-1)�C(19-2)����
�@�i�x�N�g���\������
�j (19-3)
������
�������Ǝ������x���̐���(����)��тт����邱�Ƃ������Ƃ����B�����̂�����͕����ɂ���ĈقȂ�B
�t�̎_�f�����̊Ԃɒʉ߂�����
�@�@�������́F�O�����E�̌����ɋɂ߂ċ�����������镨���B(�S�C�R�o���g�C�j�b�P���Ȃ�)
�@�@�펥���́F�O�����E�̌����Ɏキ��������镨���B(�A���~�j�E���C�����C�_�f�Ȃ�)
�@�@�������́F�O�������Ɣ��̌����Ɏキ��������镨���B(���C���C���f�Ȃ�)
�����̂̓��������Ǝ��EH�̊Ԃ� B����H �̊W������BB���������x(�P�ʂ� Wb/m2��T(�e�X��))�Ƃ����B
��������������0�{��m�̊W������B��m�͗U�d�̂̕��ɗ��ɑ������鎥�����ŁC�P�ʂ���0�Ɠ���
[H/m]�ł���)�B�펥���̂Ń�m��0�C�������̂ł̓�m��0�ł���B�������̈ȊO�̏�E�������̂Ń�m�͂�����������Ȃ̂ŁC��������́C�펥���̂�P�Ɏ����̂ƌĂԂ��Ƃ�����B
���E�C�d�E�̔�r
�@ �������̓d�C������̂ɑ��āC��킾���̎��C�͂Ȃ��B
�A���C�ɂ͓d�C�̓��̂ɓ�������̂͂Ȃ��B
�B�������̂ɑΉ�������͓̂d�C�ɂ͂Ȃ��B
�P�X�|�Q �d���̍�鎥�E
�����ɗ����d������鎥�E�����߂���@�Ƃ��Ď��̕��@������B
�@ �r�I�E�T�o�[���̖@��
�@�@�d���f��(�d��I �Ɣ�������ds�̐�)�̐����鎥�E��\���@���B
�@�@�d��I �̗���Ă��铱���̈ꕔds�̒����̕���AA'���CP�_�ɐ����鎥�E�̋���dH��
�@�@�@�@(A/m) (19-4) �ŕ\�����B
r �͓d���f�Ђ���P�_�܂ł̋����C�� ��AA'�̕�����r �̕����̂Ȃ��p�x�BdH �̌����́C�d���̗�����������r �̌����ɉE�˂����܂킵�C�E�˂��̐i�ތ����ł���B
�@�@��
��
�̊O�ςŗ^������B
�� ���̎��̒��� �~ ��
�x�N�g����
�x�N�g���̊O�ς������B
���E�̌����́C�d���̌�������r �̌����ɉE�l�W���Ƃ��E�l�W�̐i�ތ����ł���B
�A �A���y�[���̉�H�藝
�@�@�C�ӂ̕Ȑ��ɉ����Ď��E�̋�����ϕ������l�́C���̌`�ɂ�炸�C�Ȑ����т��d���̑㐔�a�ɓ������B
(�u�d���ɂ���Đ��������E���ŔC�ӂ̕Ȑ��ɉ����ĒP�ʎ���(�PWb)�̐��̎��ɂ����E�ɍR���ĂP��������Ƃ��̎d��W�́C�Ȑ����т��d���̑㐔�a �Ɠ������v
�@�@(19-2)����F��mH ��m��1Wb�Ƃ��� �d��W��H�~��������
�@�@�@(�ۂ̂����ϕ��L���͕Ȑ��̈����ϕ����邱�Ƃ�\���B)
�B �A���y�[���������̖@��
�@�@�Ȑ���H�ɓd��I�������Ƃ��ɐ����鎥�E�́C�Ȑ������Ƃ��C���̖ʂɐ����Ɏ����̋�����0I�Ŏ������ꂽ���琶���鎥�E�ɓ������B
�d���̍�鎥�E�̗�
��1 �\�����������d��
�@�@�@�A���y�[���̉�H�藝����
�d��I�ɐ����ȕ��ʓ��̓d���𒆐S�Ƃ������ar �̉~�ɉ�����1(Wb)�̎��ɂ����������Ƃ��C�͂�H (N)�C�ړ�������2��r (m)������
�@�@�@�@�@�@�d����H�~2��r��I ��(A/m) (19-5)
�@�@�@�@�@�@()
���E�̌����́C�E�˂��̐i�ތ�����d���̌����ɍ��킹���Ƃ��C�E�˂��̂܂������Ɉ�v����B������E�˂��̖@���Ƃ����B
�r�I�E�T�o�[���̖@����������߂��
�@�@�@�@�@�@
��2 �~�`�d��
�@�@�@�r�I�E�T�o�[���̖@������
�@�@�@�@�@�@
�@�@�@�@�@�@z��0�̏ꍇ�C�Cn�����ł�
(19-6)
�~�̒��S�̎��E�̌����́C�~�d���̌����ɉE�˂����܂킷�Ƃ��ɁC�E�˂����i�ތ����Ɉ�v����B������E�˂��̖@���Ƃ����B
��3 �\���m�C�h(�P�ʒ�������̊�����n)
�\�������\���m�C�h���l����ƊO���̎��E�̓\���m�C�h�ɕ��s�ł���B�}�̎��E�����ꂼ��H1�CH2�C����l �̕����ɂ��čl����ƁC �A���y�[���̉�H�藝����C
�@�@�@�@�@H1l�|H2l��0 �� H1��H2
H2�̑���ɏ\���������l����ƁCH1��H2��H3����� ��H����0 ����C�\���m�C�h�������܂ޕ�H�ōl�����
�@�@�@�@�@�@�@�@Hl�|0��nl�EI �� H��nI [A/m] (19-7)
�d���̍�鎥�E�̗�
�@�@�@
�@�@�@�@
�@�@ �����d�� �@�@�@�@�@�@�@�@�@ �@�@�@�@�~�`�d�� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�\���m�C�h
�P�X�|�R �d�������E������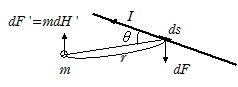
�����d��I���p�x�ƁC����r�̈ʒu�ō�鎥�E�� dH' �Ƃ���ƁC�r�I�E�T�o�[���̖@������
�@�@�ł���B
�����Ɏ���m��u���ƁC����m����� dF ' ��
�ł���B����C����m�������̒���ds�����ɍ�鎥�EH���ł���CdF' �̔���p�̗�dF�͐}�̉������ł���B|dF|��|dF'|����
�@�@|dF|��|dF '|��
������B�͎������x�Ő^�ł�B����0H�̊W�ɂ���B
����l �̓����ɗ����d��I �����E������F�̑傫����
�@�@�@�@�@�@F��IlBsin�� (19-8)
F�̌����͓d�� I�̌������玥�EB�̌����� �E�˂����܂킵�C�E�˂��̐i�ތ����B�܂��́C�E�}�Ɏ����t���~���O����̖@���ɂ��B
�@�@�@�@�@�x�N�g���̌�����
��
�x�N�g���̊O�ςŗ^������B
�x�N�g���\���������
�~
��L�̎Q�l�Ɠ������C���̎��̒��� �~ ��
�x�N�g����
�x�N�g���̊O�ς������B
(19-8)����B�̒P�ʂ�[B]��[F/Il]��N/A�Em�ł���B�܂��������xB�ŕ\�����E�́C�P�ʒ����E�P�ʓd�����͂��鋭���������Ă���B
�P�X�|�S �^������דd���q�����E������ 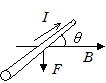
�E�}�̂悤�ɁC����l�̕����ɗ����d��I�����EB������F��
�@�@�@F��IlBsin��[N]
�ŗ^�����邪�C���̓������̓d�q���x��n[m�|3]�C�����̒f�ʐς�S[m2]�C�d�ׂ�e[C]�C�d�q�̑��x��v[m/s]�Ƃ���ƒ���l [m]�̒��ɂ���d�q�̐���nS l ������C�d�q�P�����E������f [N]�́CI��vSne(18-1�d���Q��)���g����
�@�@�@�@(19-9)
�ŗ^������B�d��q[C]�̉דd���q�����EB[N/Am]������f ��
�@�@�@ f��qvBsin�� (19-10)
�ŗ^������B��������[�����c�͂Ƃ����B
�@�@��
��
�̊O�ςŗ^������B�x�N�g���\�������
��q
�~
���̎��̒��� �~ ��
�x�N�g����
�x�N�g���̊O�ς������B
���[�����c�̌�����q��0 �̏ꍇ�C�דd���q�̑��xv �̌������玥�EB�̌����ɉE�˂����܂킵�C�˂��̐i�ތ����Bq��0 �̏ꍇ�͋t�̌����ɂȂ�B���[�����c��f �͓d��C���ꂩ���̘͂a��e(
�{
�~
)�ł��邪�C�����ł͎��E�����͂������l����B
��1 ��l�Ȏ��EB�̒��ŁC���E�ɐ����Ɏ���m�C�d��q(��0)�̉דd���q�����xv�ʼn^�����͂��߂��B���̌�̉^���ɂ��Ę_����B
�� �דd���q��v��B�ɐ����Ȑ}�̌�����f��qvB�̗͂���B
���̗͈͂��ŁC���v�̌�����ς��邽�߂����ő�����ς��邱�Ƃ͂Ȃ��B�܂�f��qvB�����S�͂ɂȂ铙���~�^��������B
�^������������C�O�����a�� r �Ƃ���Ɖ����x�� v2 / r �ł���C
(���)
�܂��C�~�^���̎���T��
2�� r��vT ��(T�͑���v�ɊW���Ȃ����Ƃɒ���)
��2 �d�q�̔�d��
�ʐ^�̔��������A�ɐ�
�}�̂悤�Ȑ^�u�ʼnA�ɂ��珉���x0�ŏo���d�q(����m�C�d�ׁ|e)��d�ʍ�V�ʼn������C�X���b�gS1����C���ʂ̗�����\�֊т��������xB�̈�l�Ȏ��E�ɐ����ɓ��˂������B�d�q�͎��E���Ŕ��ar �̉~�O����`���C����������C�X���b�gS2����o�Ă��邱�Ƃ����o���ꂽ�B�d�q�̔�d��e�^m�����߂�B
�� �d�E�̂����d�����d�q�̉^���G�l���M�[�ɂ��ׂĕς�邩��C�d�q�̑�����v
�Ƃ���ƁC eV��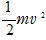
���E���ł̓��[�����c�͂����S�͂ɂȂ铙���~�^�������邩��
��������� �d��q�̓d�q�ȊO�̏ꍇ�ł����̊W�͐��藧����Cq/m�����������q�ł�(V�CB����)r �������ɂȂ�C���ʕ��͊��͂��̌������g�������u�ł���B
�E�}�̂悤�ɒ����̂̓��̂܂��͔����̂ɓd��I �𗬂��C����ɒ�����������Ɉ�l�Ȏ��EB��������B
�@�דd���q�����̏ꍇ�C���[�����c�͂�}�̉������Ɏ����̂̉��ʂ����C��ʂ����ɑѓd����ʂ��牺�ʂɌ������d�E��������B���̓d�ׂ͐������d�E����}�̏������qE�̓d�C�͂��C����ƃ��[�����c�͂��肠���ēd�ׂ͒��i����B
�@�d�ׂ����̏ꍇ(n�����̂̏ꍇ�Ȃ�)��Va��Vb�C
�d�ׂ����̏ꍇ(p�����̂̏ꍇ�Ȃ�)��Va��Vb�ɂȂ�B���̂悤�ɁC���E���̓��́C�����̂ɓd���𗬂��ƁC�דd���q�����[�����c�͂��āC���E�C�d���ɒ�����������ɓd�E�������錻�ۂ��z�[�����ʂƂ����B���̓d�E�̌����ɂ���ĉדd���q�̐����C�d�ז��x�C�������x�Ȃǂ�����ł���B
�P�X�|�U ���s�d���Ԃɂ͂��炭��
�E�}�̂悤�ɁC�^�ŋ���r [m]�u�ĂĒ�������������P�CQ�ɂ��ꂼ��I1�CI2[A]�̓d�����C���������ɗ����B���̂Ƃ��CP�𗬂��d��I1��Q�̈ʒu�ɍ�鎥�����x�̑傫��B1[N/A�m]���ł���B
����Q�̒���l [m]�̕����͂��̎��E�����̑傫���̗͂���BF�̌����͉E�˂��̖@������}�̌����ł���B
�@���̂Ƃ��C��p����p�̖@������C����P��Q����傫��(19-11)
�̗͂��C�}�̌����ɂȂ�B���̂��Ƃ���C�݂��ɂ��Ȃ������ɓd���𗬂��ƈ��͂��͂��炭���ƂɂȂ��BP�CQ�ɗ����d���̌������݂��ɔ��Ό����ɂ���ƁC�˗͂��͂��炭�B
[�d���̒P��]
�^�ŋ���1[m]�u�ĂĒ��������s�����ɓ������傫���̓d���𗬂��C����1[m]������ɓ����͂̑傫�����C2�~10�|7[N]�̂Ƃ��C�������傫���̓d����1[A]�ƒ�߂�B���������āC(19-11)����I1��I2��1[A]�Cr��1[m]�Cl��1[m]�Ƃ��������C
�^��̓�������0���ł���B
19-2 �d���̍�鎥�E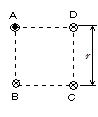
��115 �^�ɂS�{�̏\���ɒ���������̓���A�CB�CC�CD�����ʂɐ����Ō݂��ɕ��s�ɒ����Ă���BA�CB�CC�CD�͐^�ォ�猩��Ɛ}�Ɏ����悤�ɂP�ӂ�r [m]�̐����`�̊e���_�����߂Ă���B����A�CB�CC�CD�𗬂��d���̑傫���͂ǂ������I[A]�ł���C���̌����͂`�ł͎��ʂ̗�����\�Ɍ����������CB�CC�CD�ł͎��ʂ̕\���痠�Ɍ����������ł���B����A�̈ʒu�ɓ���B�CC�CD�𗬂��d�������鎥��������������̂̋��������߂�B
��116 �Q�{�̕��s�Ȓ�������A�CB�ƂP�����̔��aR�̃R�C��C���z�u����Ă���B����A�ɖ��̌����ɁC1.0A�̓d��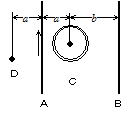 �𗬂����B�������Ca��0.10m�Cb��0.20m�CR��0.050m�Ƃ���B
�𗬂����B�������Ca��0.10m�Cb��0.20m�CR��0.050m�Ƃ���B
(1) ����A���狗��0.10m���ꂽ�n�_D�̎���̋���H�����߂�B
(2) ����B�ɂǂ������(���������������)�ɉ�A�̓d���𗬂��ƁCD�_�̎���̋�����0�ɂȂ邩������B
(3) ����A�ɖ�������1.0A�C����B�ɔ��Ε�����3.0A�̓d���𗬂��Ƃ��C�R�C���̒��SO�̎����0�ɂ��邽�߂ɂ́C
�R�C���̂ǂ�������Ɂi���v�܂�肩�����v�܂��Ɂj��A�̓d���𗬂��悢��������B
��117 �}�̂悤��x y���ʏ�̂Q�_P(�|a�C0)�CQ(a�C0)��ʂ�Cx y�ʂɐ����ȂQ�{�̒������k1�C�k2������B ���̓����ɏ�����ɓ������d��I �𗬂��B
���̓����ɏ�����ɓ������d��I �𗬂��B
(1) ���_O(0�C0)�ɂ����鎥��̋����͂����炩�B
(2) �_(0�Ca)�ɂ����鎥��̌����������傫�������߂�B
19-3 �d�������E������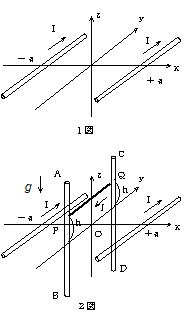
��118 �P�}�̂悤�ɐ^��y���ɕ��s��x���}a�Cz���O�ɌŒ肳�ꂽ�\�������Q�{�̓����Ɂ{y�����̓d��I�𗬂��B�Ȃ��C�������xB�Ǝ��EH�̊Ԃɂ͐^��̓�������p����B����0H�̊W������B
(1) �������xB��x�����̐�����Bx�Cz�����̐�����Bz�Ƃ���x����ɂ�����Bx��Bz��x�̊��Ƃ��āC�܂�z����ɂ�����Bx��Bz��z �̊��Ƃ��Ă��ꂼ�ꎮ�ŏ����B
(2) ��̌��ʂ����Ƃɂ���x z���ʓ��ɂ����鎥�͐��̂����܂��Ȍ`����ь�����}������B
�@����,�Q�}�̂悤��,����m,����l �̓��̖_PQ��y z���ʓ�(x��0)�ɂ�����y���ɕ��s�Ȍ`���ۂ����܂�z�����ɂȂ߂炩�ɂ��ׂ邱�Ƃ��ł���悤�ȑ��uAB�CCD��݂��顂��̑��u��ʂ��ē��̖_PQ�Ɂ|y�����̓d�� J �𗬂��B�Ȃ��C���uAB�CCD�𗬂��d������鎥�E�͖����ł�����̂Ƃ���B
(3) ���̖_PQ��x y���ʂ���̍�����h �Ƃ���Ƃ��C���̖_PQ�����E�����͂̌����Ƒ傫�������߂�
(4) �|z�����ɏd�͂��͂��炭�Ƃ��C���̖_PQ�Ɏ��E����͂��炭�͂Əd�͂��荇���ē��̖_���Î~�����B
�@���̂Ƃ����̖_PQ�ɂ͂��炭�͂̂荇���̎��������B�܂��C���̎���h�ɂ��ĉ����ē��̖_PQ���荇������h�����߂�B�܂��C�d�͉����x��g�Ƃ���B
(5) ���̖_PQ�ɗ����d�������������Ă����Ƃ₪�ē��̖_���荇���̈ʒu�������Ƃ��ł��Ȃ��Ȃ�B���̖_PQ���荇���̈ʒu�������߂̓d��
J�̍ŏ��l�����߂�B
19-4 �^������דd���q�����E������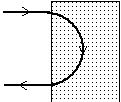
��119 �E�}�̘g���ɂ́C���ʂɐ����Ɉ�l�Ȏ��E���������Ă���B ���܁C��������C����1.7�~10-27[Kg]�C�d��1.6�~10�|19[C]�̗z�q���C2.0�~105 [m/s]�̑����Ŕ��ł��ĉ~�^�������B�������x��0.40[T]�Ƃ���B
(1) �z�q�ɓ����͂̑傫�������߂�B
(2) ���E�̌�����![]() ,
,![]() �œ�����B
�œ�����B
(3) �~�O���̔��a�����߂�B
(4) ���E�������Q�{�ɂ����ꍇ�C�z�q�̋O���͂ǂ̂悤�ɕω����邩�B
(5) ���x�������Q�{�ɂ����ꍇ�C�����͂ǂ̂悤�ɕω����邩�B
��120 �}�̂悤�Ɏ������xB[Wb/m2]�̈�l�Ȏ���̒��ŁCB�̕����ɑ�����[rad]�̊p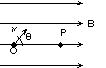 �x�������đ���v[m/s]�ʼn^�����Ă��鎿��m[Kg]�C�d��q[C](q��0)�̉דd���q������B
�x�������đ���v[m/s]�ʼn^�����Ă��鎿��m[Kg]�C�d��q[C](q��0)�̉דd���q������B
(1) ���̉דd���q��B��v�ɐ����Ŏ�͂̑傫���͉�[N]���B
(2) ���鎥�͐���ɓ_�n����o���������̉דd���q���点��^�������Ď��ɍĂт��̎��͐���̓_�o��ʂ�܂łɗv���鎞�Ԃ͉�[s]���B
(3) ����OP�̒����͉�[m]���B
(4) ���̉דd���q��O����P�Ԃł点���ɑ����������͉�[m]���B
(5) �������x��2B�ɂ����ꍇ�C(2)�ŋ��߂��l�͉��{�ɂȂ邩�B
��121 ���̕��͂�[ ]��K���ȕ������邢�͎��Ŗ��߂�B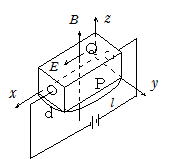
�����̂������m�^�����́i����l�C��d�C����h�j��}�̂悤�ɒu���C����x���̐��̕����ɋ���E�P�̓d���������ƁC���̔����̂̓d���̒S����(�L�����A�[)�ł��鎩�R�d�q�� [�P] �̕����Ɉړ����ēd���������B���̂Ƃ�z���̐��̕����Ɏ������xB�̈�l�Ȏ����������C�L�����A�[�� [2] �̕����Ƀ��[�����c�͂��邱�ƂɂȂ�B���̂��ߔ����̂̎�O�̖�P�� [3] �ɑѓd���C���������̖�Q��
[4] �ɑѓd���� [5] �̕����ɓd�ꂪ������B���̓d��̋���E2�́C�L�����A�[���d�ꂩ���͂ƃ��[�����c�J�Ƃ̂肠���ɂ���čŏI�I�Ɍ��܂�B���̂悤�ɔ����̂Ɏ���������Ă��C�L�����A�[�ɂ͂��炭��̗͂��肠���C�L�����A�[��[6]
�̕����Ɉ��̑����Œ��i���Ă���ƍl���Ă悢�B
���[�����c�J�Ɠd��E2�ɂ��͂Ƃ̂肠������C�����̓��ł̃L�����A�[�̑��������߂�� [7] �ƂȂ�̂ŁC�����̂̒P�ʑ̐ϓ�����̃L�����A�[�̐���n�C�d�C�f�ʂ�e�Ƃ���C�����̂𗬂��d���̑傫���� [8] �̂悤�ɕ\�����B
�@ ����C�����̂̒�R�������Ƃ����,�����̂𗬂��d���̑傫���̓I�[���̖@������ [9] �Ə�����B [8] �� [9] �ŗ^������d���̑傫���͓��R�������C���ꂩ��m�^�����̂̃L�����A�[�̐����xn���d��̋���E1��E2�̔���g���� [10] �Ƃ��ĕ\����邱�ƂɂȂ�B
19-6 ���s�d���Ԃɂ͂��炭��
��122 (1) �^�Ŗ����ɒ���������̓����ɋ���I[A]�̓d��������Ă���Ƃ��C��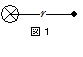 ������̋���r[m]�̓_�ɂ����鎥�E�̋��������߁C���̌�����}�P�ɋL������B�������C
������̋���r[m]�̓_�ɂ����鎥�E�̋��������߁C���̌�����}�P�ɋL������B�������C![]() ��͓d�������ʂɐ����ɕ\���痠�֗���Ă��邱�Ƃ������C
��͓d�������ʂɐ����ɕ\���痠�֗���Ă��邱�Ƃ������C![]() ��͂��̋t�̏�Ԃ������B
��͂��̋t�̏�Ԃ������B
(2) ����2d[m]����ĕ��s�ɒu���ꂽ�Q�{�̖����ɒ���������̓����ɋ���I[A]�̓d�������Ό����ɗ���Ă���ꍇ�ɂ���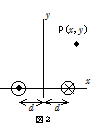 �l����B
�l����B
(�) x���Cy����}�Q�̂悤�ɂƂ�C�����d����z�����Ƃ���Bx y���ʏ�̓_P(x�Cy)�ɂ����闼�d���ɂ�鍇�����E�̋�����x�Cy�����ɕ����ċ��߂�B
(�) �E���̒����d���͍����̒����d���ɂ���Ď��E����͂���B�����̒P�ʒ����ɓ����͂̑傫�������߂�B
���̌�����}�Q�ɋL������B�������C�^��̓���������0[N/A2]�Ƃ���B
(�) �����̒����d����(�)�Ɠ��l�ɗ͂���̂ŁC�Q�����d���̊Ԃɂ͗͂������B���̗͂͐˗͂��C���͂��B
��123 ������̓����ɓd���𗬂��Ɠ����̂܂��Ɏ��E��������B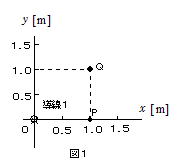 �^�ōl���悤�B�^��̓���������0[N/A2]�Ƃ���B�}�Ɏ����悤�ɁC��{�̒�����̓�����x�|y���ʂɐ����Ɍ��_��ʂ�悤�ɒu���B�����1�ƌĂԂ��Ƃɂ���B�ȉ��C�����̑����͖����ł�����̂Ƃ��顂܂����W�̒P�ʂ̓��[�g��[m]�ł��顓����P�Ɏ��ʂ̕\���痠�ɓ˂������������I1[A]�̓d���𗬂��B
�^�ōl���悤�B�^��̓���������0[N/A2]�Ƃ���B�}�Ɏ����悤�ɁC��{�̒�����̓�����x�|y���ʂɐ����Ɍ��_��ʂ�悤�ɒu���B�����1�ƌĂԂ��Ƃɂ���B�ȉ��C�����̑����͖����ł�����̂Ƃ��顂܂����W�̒P�ʂ̓��[�g��[m]�ł��顓����P�Ɏ��ʂ̕\���痠�ɓ˂������������I1[A]�̓d���𗬂��B
(1) �_Q(1,1)�ł̎��E�̋��������߂�B
����ɁC�_R(k�C0)(k��0)��ʂ� x�|y���ʂɐ����ȂQ�{�ڂ̒�����̓����C�����Q��ݒu���悤�B�����Q�ɂ͎��ʂ̗�����\�ɓ˂������������I2[A]�̓d���𗬂��B
(2) �����Q�̒���l [��]�̕��������E�����͂����߂�B
(3) �����Q���P�ƕ��s�ɕۂ��������P�Ƃ̋��������ɂ����܂�,�����P�̂܂�������������������B���̂Ƃ��C���E�͓����Q�ɗ͂��y�ڂ��Ă���̂ɂ�������炸���̗͂̂����d����0�ł������B���̗��R���������B
�z�[�� ���j���[ �Ód�E �R���f���T�[ ������H ���E �d���U�� ��