�z�[�� ���j���[ ![]() �Ód�E �R���f���T�[ ������H ���E �d���U�� ��
�Ód�E �R���f���T�[ ������H ���E �d���U�� ��
�Q�O�|�S �� (alternating current)
(alternating current)
�𗬔��d�@�̌����͈��̊p���x���ŃR�C�������E�̒��ʼn�]������ƁC�R�C�����ɐ����g�̓d��(�N�d��)����������B�u�Ԓlv�͍ő�l��V0�Ƃ����v��V0sin��t�ŗ^������B
�𗬂�d�C��RR�C�R���f���T�[C�C�R�C��L�̊e�f�q�ɗ������ꍇ�C�����̏ꍇ�ɂȂ������I�Ȍ���(���Ƃ��Γd���d���̈ʑ��ω�)���N����B�ȉ��Ɋe�f�q�ł̓d���C�d���C�܂������̈ʑ����ɂ��čl����B
�Q�O�|�S�|�P�d�C��RR�̓������𗬉�H
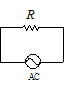
�}�̂悤�ɓd�C��R(��R�lR[��])�Ɍ𗬂𗬂��B�d�C��R�ł͓d��V�Ɠd��I �Ɉʑ��̂��ꂪ�N���邱�Ƃ͂Ȃ��̂ŁC�d���d����v��V0sin��t�Ƃ���ƁC�d��I �͍ő�lI0��������C
�ŗ^������B
�d�C��R�ł̓d��P��P��VI��V0I0sin2��t��V0I0(1�|cos2��t)
�d�͂̎��ԕ��ϒl��
��������d���C�d���̎����l�Ƃ����B���̎�����킩��悤�ɁC�����l�͓d�͂̎��ԕ��ϒl���Ɠ����`�ŕ\�����Ƃ̂ł���l�Ƃ������Ƃ��ł���B�𗬂ł͓��ɒf�肪�Ȃ�����d���C�d���͎����l���g���B
�@�܂��C�d���̎���̎��ԕω���I2��I0sin��t�ł���C���̕��ϒl���ł���B���ꂩ��
�ƕ\�����Ƃ��ł���B�܂�C�d���̎����l�͓d���̎��敽�ϕ�����(�P�T�C�N���ɂ킽��d���̎���̕��ϒl�̕�����)���C�����l�̂�����̈Ӗ��ł���B
�@100[V]�̓d���Ƃ����ꍇ�C�����l��100[V]�C�ő�l��100[V]�ł���B�d���ɂ��Ă����l�ɁC�𗬓d��1[A]�Ƃ͎����l��1[A]�C�ő�l��
[A]�ł���B
�d���d����v��V0sin��t�Ƃ���B�R�C���Ɍ𗬓d����ڑ�����ƁC��H�ɂ͓d���d��v�ƂƂ��ɁC�R�C���ɂ��U���N�d��v ' ��������̂�,�L���q�z�b�t�̑�Q�@������
�@�@�@v�{v'��iR��0 (20-6)
(�� �d���~��iR��R���O������0)
�����œd��i ���d���ɑ��Ăǂ̂悤�Ȉʑ��ω������邩���ׂ邽�߂�
�@�@�@i��I0sin(��t�{��) (20-7)
�Ƃ���B���͓d���Ɠd���Ԃ̈ʑ����ł���B
v ' �������� v�{v '��V0sin��t�|LI0��cos(��t�{��)��0
�@�@�� V0sin��t��LI0��cos(��t�{��)
���̎������ԂɊW�Ȃ����藧���߂�
�@�@V0��L I0�� ��(20-8)
L�����U�����A�N�^���X(inductive reactance)�Ƃ����C�d���̗����ɂ����������ʂł���B
�P�ʂ�H/s��(Vs/A)/s���� (H(��ذ)��Vs/A�@20-3���ȃC���_�N�^���X�Q�� )
�܂��Asin��t��cos(��t�{��)�����藧����Ӂ������(20-7)����
�@�@�@i��I0sin(��t)��
�܂��R�C���ɗ����d���͓d�����ʑ����x��Ă����B
���̈ʑ������E�}�̂悤�Ɏ����B
�d�͂̏u�ԒlP��
�d�͂̎��ԕ��ϒlP�� P��0 (��)
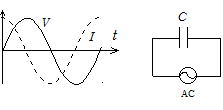
�d���d����v��V0sin��t�Ƃ���B�R���f���T�[�Ɍ𗬓d����ڑ�����ƁC��H�ɂ͓d���d��v�ƂƂ��ɁC�R���f���T�[�ɒ~����ꂽ�d��q�����d�ʍ�v' ������B�d�C��R���l���Ȃ��ƁC�L���q�z�b�t�̑�Q�@������
�@�@�@v�|v '��0 (20-9)
�d��q�C�d��i�C�d�C�e��C�̊Ԃɂ�
�@q��cv '�C�̊W������B�d��i ���d���ɑ��Ăǂ̂悤�Ȉʑ��ω������邩���ׂ邽�߂�
i��I0sin(��t�{��)�Ƃ���ƁC
�܂��C�ł���B
����炩��@
���̎������ԂɊW�Ȃ����藧���߂�
�@�@�@�@(20-10)
1/C�����e�ʃ��A�N�^���X(capacitive reactance)�Ƃ����C�R���f���T�[�̓d���̗����ɂ����������ʂŒP�ʂ̓��ł���B
�܂� cos��t��sin(��t�{��)����C�d���Ɠd���̈ʑ������Ȃ̂œd����i��I0sin(��t�{
)��I�Ocos��t �@(20-11)
�܂��R���f���T�[�ɗ����d���͓d�����ʑ����i��ł���B
���̈ʑ������E�}�̂悤�Ɏ����B
�d�͂̏u�ԒlP��
�d�͂̎��ԕ��ϒlP�� P��0 (��)
�@ �����H(series connection circuit)
R�CL�CC���ꂼ��ɗ����d�����������C�����i��I0sin��t�Ƃ���BR�CL�CC���ꂼ��̓d����VR�CVL�CVC�Ƃ����
vR��I0R�Esin��t
vL��
vC��
�ʑ��̈Ⴂ���E�}�Ɏ����B�d���d��V�͉E�}�̂悤�ɂ��ꂼ��̃x�N�g���a����
(20-12)
�������@ (20-13)
���C���s�[�_���X�Ƃ����B
V��I�̂Ȃ��p�x�����Ƃ���ƁA�ʑ��p��(20-14)
�ŗ^������B��H�𗬂��d��I ��
�@�@�@(20-15)
�ŗ^������B�܂��Ccos�����͗��Ƃ����B�͗����g���ĕ��ϓd�͂�\�����Ƃ��ł���B
�@P��V�EIcos�� R�����̏ꍇ(����0)�C��V I
L�CC�����̏ꍇ(�����C�|
)�C
��0
�����H�ł̋��U��H(reasonance circuit)
�@(20-15)�������H�𗬂��d��I �͌𗬂̊p�U��������2��f�@(f �͎��g���C�P�ʂ�Hz)�ɂ���ĕω�����B���ꂪ�ŏ��l�܂�@L����1�^C���̂Ƃ���I���ő�l�ɂȂ�B���̂Ƃ��̎��g��f0(���U���g���Ƃ���)��
�@�@�@�@�@(20-16)
R�CL�CC���ꂼ��̓d����iR�CiL�CiC�Ƃ���ƁC�d���͑S�ē������B
�����v��V0sin��t�Ƃ���ƁC�d���𗬂��d��i ��
�@�@�@�@�@i��iR�{iL�{iC �ł���
�@�@�@�@�@
������(�O���t�Q��)
�@ �@�@�@�ł���B
�����i��I0sin(��t�|��) (I0�͍ő�d���C���͒萔)�Ƃ����
�@�@�@�@�@
�����ɓƗ����Ă��̎������藧���Ȃ���Ȃ�Ȃ�����
�@�@�@�@�@
�@�@�@�@�@��
�@�@�@�@�@��
�����H�ł̋��U��H(parallel resonancecircuit)
�@�@(20-17)�������H�𗬂��d��I ��L����1�^C���̂Ƃ���I ���ŏ��l�ɂȂ�B���U���g��f0��
�@�@(20-18) ���U�Ȑ��͉E�}�B
�Q�O�|�T �d�C�U��(electric vibration)
�����}�̂悤�ȉ�H�����C�X�C�b�`�����ɓ���ăR���f���T�[���[�d����B���ɃX�C�b�`���E�ɓ���ăR���f���T�[C�ƃR�C��L���Ȃ��Ɖ�H�ɂ͉E���}(�����U���̏ꍇ)�̂悤�ȓd�C�U���������B����̓R�C���ɒ~����ꂽ�G�l���M�[���R�C���Ƃ̊ԂŌ݂��ɓ���ւ�邽�߂ɋN���邽�߂ł���B�R���f���T�[�̓d�ׂ�q�C�d����i�Ƃ����(�����̓R���f���T�[�̓d�ׂ���������Ɠd�����������邱�Ƃ�����)�ł���B�R�C���̎��ȃC���_�N�^���X��L�C�R���f���T�[�̐Ód�e�ʂ�C�Ƃ���ƁC�L���q�z�b�t�̑�Q�@������(20-19)
(20-19)����͊w�n�Ɣ�r����ƈȉ��̒ʂ�B
�d�C�n �d��q �d��i L 1/C �R�C���̃G�l���M�[ �Ód�G�l���M�[ �͊w�n �ψ�x ���xv ����m ���萔k �^���G�l���M�[ �e���G�l���M�[
���̂��Ƃ���C�̂悤�ɑΔ䂳����ƁC�͊w�n�̒P�U�����d�C�n�̓d�C�U���Ɠ����`���ŕ\����邱�Ƃ��킩��B�܂�C�͊w�n�ŒP�U���̐U�����������x���|��2x�Ƃ��ĐU���������߂��Ɠ��l�ɂ��āC(20-19)���̉E�Ӂ��|��2q�Ƃ����������ߐU����f ���v�Z����ƁC
�ƂȂ�B�����(20-18)���ƑS�������ł���B
�E�}�͔�(R��0)�̏ꍇ�̓d��q�C�d��i�Cq2(�R���f���T�[�̐Ód�G�l���M�[�ɔ��)�Ci2(�R�C���̃G�l���M�[�ɔ��)�̃O���t�ł���B�R���f���T�[�ƃR�C���̊ԂŃG�l���M�[������ւ���Ă���l�q���킩��B����̃G�l���M�[���ő�̂Ƃ��ɂ�������̃G�l���M�[���ő�ɂȂ��Ă���Bt��0�ł̓d�ׂ�q0�C�d���̍ő�l��I0�Ƃ���ƁC
�@�@�@�@�ł���B
�Q�O�|�U �ψ���(voltage transformer)
�E�}�̂悤�ɓS�S�ɂP���R�C��(������n1)�C�Q���R�C��(������n2)�������C�P���R�C���Ɍ𗬓d����������ƁC�R�C���ɗ����@�@�@�𗬓d���̕ω��ɔ����āC�S�S�̒��Ɏ��ԓI�ɕω����鎥������������B�����͓S�S����قƂ�ǘR�ꂸ�ɁC�Q���R�C���̒���ʂ�̂ŁC�Q���R�C���ɗU���N�d�͂���������B���̂Ƃ��C�����ɂP���R�C���ɂ͎��ȗU���ɂ��t�N�d�͂���������B
�@�P���R�C���̋t�N�d��v1�C�Q���R�C���ɐ�����U���N�d��v2�͎�������t �Ԃɇ����̊����ŕω�����Ƃ�
�@�@�@�@�ł���B���̋t�N�d�͂ɂ荇���𗬓d��v1���P���R�C���ɉ��������Ȃ���Ȃ�Ȃ��B
������C�d���̎����l�����ꂼ��V1�CV2�Ƃ����
�ƂȂ�B���ꂼ��̓d���͊������ɔ�Ⴗ��B
����ł��ꂼ��ɗ����d��I1�CI2�͓d�͂̑������Ȃ��Ƃ����V1I1��V2I2 �����ł���B�������܂ő��d����ꍇ�r���̓����ŃW���[���M�iI 2Rt�j����������̂ŁC��������������邽�߂ɁC��R�lR�Ɠd�� I �����������邽�߂ɁC���d���C��d���ɂ��đ��d����B
20-1 �d���U���̖@��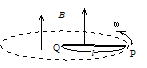
��124 ����������Ɏ������xB�̎��E������B����l �̋����_PQ���CQ�_�𒆐S�ɂ��Đ����ʓ����p���x���ʼn�]���Ă���BPQ�̋N�d�͂͂����炩�B�܂�P�CQ�̂�����̓d�ʂ��������B
��125 �}�Ɏ����悤�ɁC0��x��L[m]�̗̈�Ɏ��ʗ�����\�Ɍ����������Ɏ������xB[T]�̈�l��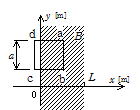 ���E������C����ȊO�̗̈�ł͎������x��0[T]�ł���B���̎��E������ӂ̒���a[m]�C�S�̂̒�R��R[��]�̐����`�̈�d�R�C�������������Cx�����Ɉ�葬�xv[m/s]�ňړ�������B���̈�d�R�C���̊e�ӂ́Cx���܂���y���ɕ��s�ɕۂ���Ă���B�܂��C��d�R�C���̈�ӂ̒���a�͎��E�̕�L����������(a��L)�B
���E������C����ȊO�̗̈�ł͎������x��0[T]�ł���B���̎��E������ӂ̒���a[m]�C�S�̂̒�R��R[��]�̐����`�̈�d�R�C�������������Cx�����Ɉ�葬�xv[m/s]�ňړ�������B���̈�d�R�C���̊e�ӂ́Cx���܂���y���ɕ��s�ɕۂ���Ă���B�܂��C��d�R�C���̈�ӂ̒���a�͎��E�̕�L����������(a��L)�B
(1) �R�C���̉E�[��x��0����x��L�{a�̓_�ɒB����܂ł̃R�C�����т�����[Wb]�i���ʗ�����\�Ɍ����������𐳂Ƃ���j���c���C����������[s]�Ƃ��ăO���t��`���B�c���C�����Ƃ��ɓK�Ȗڐ��������B
(2) �R�C���̉E�[��x��0���� x��L�{a �̓_�ɒB����܂ł̃R�C���ɗ����d�� I [A]���C�����ɃR�C���̉E�[�̈ʒu�� x �Ƃ��āC�O���t��`���B
�������C�ォ�猩���}�ɂ����Ĕ����v�܂��ɗ����d���𐳂Ƃ���B�܂��CI �̑傫���̍ő�l�����߂�B
(3) �R�C���̕ӂ��������E������F [N]���C�������R�C���̉E�[�̈ʒux �Ƃ��ăO���t�ɕ`���B�������E�����𐳂Ƃ��C�l����x �͈̔͂�(2)�� �����Ƃ���B
��126 �������xB�̉���������̎��E������B�E�}�̂悤�ɊԊul�̃��[����ɂȂ߂炩�ɓ�������m[Kg]�̒�R�̂Ȃ��������̂��Ă���B�d�r�̋N�d�͂�E[V]�C��R�q�̒�R�l��R[��]�ł���B��H�𗬂��d���̍�鎥�E�C�d�r�̓�����R�͖����ł���B
(1) �X�C�b�`�r����ꂽ����C�����ɗ����d�������߂�B
(2) �X�C�b�`�r����ꂽ����C���������E�����͂����߂�B
(3) �����̑�����v[m/s]�ɂȂ����Ƃ��C�����ɗ����d�������߂�B
(4) (3)�̏u�ԁC�����̉����x�����߂�B
(5) �\�����Ԃ��o�߂�����́C�����̑���v�������߁C�����������n�߂Ă��瑬����v���ɂȂ�܂ł̎��ԂƑ����̊W�������O���t��`���B
��127 �}�̂悤�ɁC����������̈�l�Ȏ��E(�������xB[T])�̒��ŁCl [m]�̊Ԋu�ŕ��s�ɕ��ׂ�ꂽ�Ȃ߂炩�ȃ��[�����C�����ʂɑ����� �̊p�x�ɕۂ��C���̏�[��R[��]�̒�R���ƋN�d�͂�E[V]�̓d�r���Ȃ��B���̃��[����Ɏ���m[Kg]�̋����_�o�p�����[���ɒ��p�ɍڂ��ĐÂ��ɕ����B�d�͉����x�̑傫����g[m/s2]�Ƃ��CR�ȊO�̓d�C��R�͂��ׂĖ����ł�����̂Ƃ���B��H�𗬂��d������鎥�E�͖����ł�����̂Ƃ���B
(1) �_�o�p������v[m/s]�ʼn��~���Ă���Ƃ��o�p�ɔ�������U���N�d�͂����߂�B
(2) (1)�̂Ƃ��C�o�p�𗬂��d��I [A]�����߂�B
(3) (1)�̂Ƃ��C�o�p�����E�����͂̑傫�������߂�B
(4) ���[�����\���������̂Ƃ���ƁC�_�o�p�̉��~���鑬���͍ŏI�I�ɂ�����ɂȂ邩�B
20-4 ��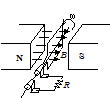
��128 �}�̂悤�ɁC�f�ʐ�S[m2]�łP�����̃R�C�����������xB[Wb/m2]�̈�l�Ȏ���̒��ɂ�����C��]���̂܂����p���x��[rad/s]�ʼn�]���Ă���B�R�C���̗��[��R[��]�̒�R�łȂ���Ă���B�R�C���ʂ�����ɐ����ȂƂ�������0�Ƃ��āC���̖₢�ɓ�����B
(1) ����t [s]�ł́C�R�C�����т�������[Wb]�����߂�B
(2) ����t [s]�ł́C�R�C���ɐ�����N�d��v[V]�����߂�B
(3) ����t [s]�ł́C�R�C���𗬂��d��i [A]�����߂�B
(4) �d���̎����lI [A]�����߂�B
(5) �d���̎����lV [V]�����߂�B
��129 �}�P�̂悤�ɓd��V��V0sin��t [V]������𗬓d�����C�X�C�b�`�r���ւ��邱�Ƃɂ��CR[��]�̒� �R�C���ȃC
�R�C���ȃC ���_�N�^���XL[H]�̃R�C���C���邢�͓d�C�e��C[F]�̃R���f���T�[�̂ǂꂩ�P�ɐڑ�����Ă�����̂Ƃ���B
���_�N�^���XL[H]�̃R�C���C���邢�͓d�C�e��C[F]�̃R���f���T�[�̂ǂꂩ�P�ɐڑ�����Ă�����̂Ƃ���B
(1) �R�C���C�R���f���T�[�ɗ���邻�ꂼ��̓d���̎����lIL�CIC��V0��p���ĕ\���B
(2) ��R�C�R�C���ł̂��ꂼ��̏���d�͂̎��ԕ��ϒlPR�CPL�����߂�B
�@�d���d��V�̔g�`���}�Q�̂悤�ł������B
(3) �R�C���C�R���f���T�[���ꂼ��ɗ����d��IL�CIC�̎��ԕω������ɕ`���B
(4) �R�C���C�R���f���T�[���ꂼ��̓d��PL�CPC�̎��ԕω���`���B
��130 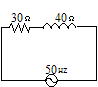 30[��]�̒�R�ƁC�U�����A�N�^���X��40[��]�̃R�C����ɂȂ��C50[Hz]�̌𗬓d���ɐڑ�������C��R�ɗ����d����0.50[A]�ł������B�K�v�Ȃ�C
30[��]�̒�R�ƁC�U�����A�N�^���X��40[��]�̃R�C����ɂȂ��C50[Hz]�̌𗬓d���ɐڑ�������C��R�ɗ����d����0.50[A]�ł������B�K�v�Ȃ�C![]() �Ƃ���B
�Ƃ���B
(1) �R�C���̎��ȃC���_�N�^���X�͉�[H]���B
(2) �R�C���ɂ�����d���͉�[V]���B
(3) �d���̓d���͉�[V]���B
��131 �𗬓d���̓d��V���}�P�̂悤�ɕω�����B�𗬓d���C10���̓d�C��R�C�R�C���k��}�̂悤�ɔz�u����B
���l�v�Z�ŕK�v�Ȃ�C�Ƃ���B�o�Ƃa�����ԂƃR�C���k�𗬂��d��I1�͐}�Q�̂悤�ł������B
(1) �d���d���̎��g�������߂�B
(2) �R�C���̎��ȃC���_�N�^���X�����߂�B
�o�Ƃ`�����ԂƐ}�R�̂悤�ɓd��I2�����ꂽ�B
(3) �R�C���k�̗��[�̓d���̍ő�l�����߂�B
(4) �d��I2�Ɠd���d���̈ʑ��������߂�B
(5) �R�C���k�̗��[�̓d���̎��ԕω���}������B
�z�[�� ���j���[ �Ód�E �R���f���T�[ ������H ���E �d���U�� ��