ホーム メニュー ![]() 静電界 コンデンサー 直流回路 磁界 電磁誘導 交流
静電界 コンデンサー 直流回路 磁界 電磁誘導 交流
【18】電流と仕事
18-1 電流(electric current)とは
電荷が電場の作用を受けて移動する現象を電流と称し,その道筋を回路(circuit)という。移動する電荷は,導体の場合は自由電子,電解質溶液の場合は正負のイオン,半導体の場合は自由電子またはホール(正孔)である。金属に電流が流れる場合,移動する実体としての自由電子は,電位の低い方から高い電位の方に移動するが,これを正電荷が高電位の方から低電位の方に移動したと考える。
電流が流れるためには,① 電場が与えられる,② 電荷が供給される,③ 電荷が自由に動けるなどの条件が必要である。電圧を与える役目をするのが電源,電源からの電流の流出口および流入口を端子という。
電流の強さ(intensity)は,導線の断面を,面に垂直に時間t [s]間に一定の電荷Q[C]が移動するとき,
(18-1) と定義される。
一定でない場合はで与えられる。
単位は1 [A]=1[C/s]である。つまり1秒間に1C(クーロン)の電荷が移動するときの電流が1Aである。単位Aはアンペールからとっている。
(注) 電流の強さは,この他に電磁力からも定義されている([磁界]19-6平行電流間にはたらく力(19-11)参照)。
1Aの電流が流れるとき,電気素量(電子1個の電荷)の大きさをe,1秒間に移動する電子の数をnとするとだから
1A=e(C)×n(個/s) だから n=1/e=1/1.6×10-19=6.3×1018(個/s) である。
18-2 オームの法則(Ohm's law)
オーム(Ohm)は1826年に針金状の導体について実験し,温度が一定なら針金に流れる電流の強さが針金の両端の電位差に比例することを発見した。導線に電流I [A]が流れ,電圧降下(電位差)がV [V],電気抵抗がR [Ω]のとき
V=IR の関係をオームの法則という。
抵抗の単位は1[Ω]=1[V/A] つまり,1[V]の電圧降下があるとき1[A]の電流が流れるような抵抗値が1[Ω]である。
18-3 電気抵抗(electric resistance)
導体中を電子などの荷電粒子が移動すると,導体を構成する原子イオンと衝突と繰
| 抵抗率(20℃)と温度係数 | ||
| 物質 | 抵抗率(Ωm) ×10-8 |
温度係数 (1/℃)×10-3 |
| 金 | 2.4 | +3.5 |
| 銀 | 1.62 | +4.0 |
| 銅 | 1.72 | +4.3 |
| アルミニウム | 2.8 | +3.9 |
| 鉄 | 9.8 | +6.6 |
| ニクロム | 109 | +0.16 |
| 炭素 | (0.2~4)×10-5 | |
| コンスタンタン* | 49 | 0.01 |
| ゲルマニウム | 0.47 | -0.05 |
| ケイ素 | 2.3×103 | -0.08 |
| *コンスタンタンは(銅55,ニッケル45%) | ||
り返す。これが電気抵抗の原因である。電気抵抗値Rは,断面積,長さ,材質,および温度によってきまる定数である。 電気抵抗は
![]() (18-2) で与えられる。
(18-2) で与えられる。
ここに,ρ[Ω・m]は抵抗率,S [m2]は抵抗線の断面積,l [m]は抵抗線の長さである。ρは材質によって決まり温度が関係する量で,
ρ=ρ0(1+αt ) (ρ0は0℃での抵抗率,α[1/℃]は温度係数,t [℃]は温度である)で与えられる。
温度係数αは純粋な金属ではおよそ1/240である。なお,1/ρを電気伝導率という。
電気抵抗は,V-I グラフが直線関係の線型抵抗(図①),曲線関係の非線形抵抗(図②)がある。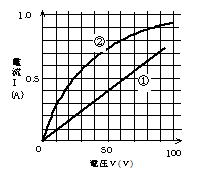 電球などが非線型抵抗の例だが,電球のフィラメントの温度上昇によってフィラメント中の原子の熱振動が激しくなり,電子の流れを妨げることが主な原因である。
電球などが非線型抵抗の例だが,電球のフィラメントの温度上昇によってフィラメント中の原子の熱振動が激しくなり,電子の流れを妨げることが主な原因である。
また,導体の断面積をS[m2],電子密度をn[個/m3],自由電子の電荷を-e[C],電子の平均の移動の速さをv[m/s]とすると,導体の断面を単位時間に通過する電子数はvSn[個/s・m2]だから,
電流の強さは
I=vSne である。
電気抵抗が ![]() になる理由
になる理由
長さl 「m],断面積S[m2]の導線に電位差V[V]をかけると,電場E[V/m]=V/l ができ,電荷e[C]の電子は力eE[N]を電場から受けるとともに,逆向きに速さvに比例する抵抗力kv(kは定数)を受ける。電子の速さは,導体を構成する原子イオンとの繰り返しの衝突で左下図のような変化をするのが,その平均値をv とする。電子が動き出してから十分時間が経過すると2つの力がつり合って等速運動をするので
eE=kv ∴ v=![]()
 電流はI=vSneとオームの法則から
電流はI=vSneとオームの法則から
I=vSne=![]() Sne=
Sne=![]()
∴ R=![]()
例 断面積S=1.0×10-6m2の導線に,電流I=1.0Aを流す。電気素量を-e=1.6×10-19C,密度ρ=9.0×103Kg/m3とする。
銅は64g中に6.0×1023個の原子があり,1個の原子に1個の自由電子をもつものとする。
(1) 電子密度nは何(個/m3)か。
{6.0×1023/(64×10-3)}×9.0×103=8.4×1028(個/m3)
(2) 電子の移動速度を求めよ。
![]()
⇒ 電子の移動速度は速いものではないのに,電灯のスイッチをいれるとなぜすぐに点くのか?
スイッチをいれると導線内に電場が電磁波の伝わる速さでできるためである。スイッチの位置にある電子が電灯まで移動しなくても電灯は点く。
![]()
18-4 合成抵抗(resultant resistance)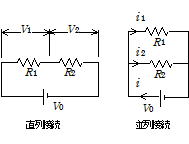
① 直列接続
それぞれの抵抗に流れる電流iは等しいから,
電圧降下V1,V2は抵抗R1,R2に比例する。電池の起電力をV0とすると
⇒ V はRに比例する
合成抵抗値をRとすると
V0=V1+V2=i (R1+R2)=iR ∴ R=R1+R2 (18-3)
② 並列接続
それぞれの抵抗の電圧降下は等しいので,それぞれの電流をi1,i2,電池に流れる電流をi,合成抵抗値をRとすると
i=i1+i2=(18-4)
V=i1R1=i2R2 ∴ i1/i2=R1/ R2 ⇒ それぞれの抵抗に流れる電流はRに反比例分配される
18-5 電流計・電圧計(current meter・volt meter)
電流計は回路に直列に入れるので,内部抵抗をできるだけ小さく,電圧計は抵抗に並列に配線するので,できるだけ内部抵抗を大きくしなければならない。
電流計
内部抵抗rAの電圧計を使って抵抗Rに流れる電流を測定する。
電源の電圧をVとすると,左図の回路に流れる電流iは
i=V/(R+rA) である。本来はi=V/Rを測定したいのだから,内部抵抗rAは
rA≪R としなければならない。
電圧計
内部抵抗rVの電圧計で抵抗Rの電圧降下を測りたい。電圧計を入れた事による影響を避けるためには,電圧計への電流の分流を最小限にすればよい。このためにはrVをできるだけ大きくしなければならない。
RとrVの合成抵抗値R' は
であり,
rV≫R とするとR'≒R である。
分流器 ・・・電流計の最大測定値を大きくするために,電流計に並列に抵抗を接続したもの
測定可能最大値i0,内部抵抗rAの電流計を使って,そのn倍の電流を測定したい場合
電流計に並列に抵抗値RSの抵抗を並列に接続し,RSに(n-1)i0を分流させる。2つの抵抗は並列なので電圧降下は等しいから
rA・i0=RS(n-1)i0 ∴ RS=→ RSが小さいほど大きな電流を測定が可能になる
例 i0=10mA,rA=9Ωの電流計で,n=10つまり100mAまで測定したい場合
RS==
=1Ω を電流計に並列に接続すればよい。
倍率器・・・ 電圧計の最大測定値を大きくするために電圧計(または電流計)に抵抗を直列に接続したもの
測定可能最大値V0,内部抵抗rVの電圧計を使って,そのn倍の電流を測定したい場合
電圧計に抵抗値RMの抵抗を直列に接続し,RMに(n-1)V0を分圧させる。2つの抵抗に流れる電流i は等しいから
例 V0=3.0V,rV=3.0KΩの電圧計を使ってn=10つまり30Vまで測定したい場合
を電圧計に直列に接続すればよい。
⇒ 電流計で倍率器を作る場合は,上記のV0をrA・i0とすればよい。電流計と電圧計の違いは内部抵抗の大きさだけである。
右図のように配線し,電池の端子電圧Vと電流i の関係を調べると右下がり直線のグラフが描ける。可変抵抗をR,i=0でのV をE,グラフの傾きをr とすると
V=E-ir=Ir (18-5)
の関係が成り立つ。Eを起電力,r を内部抵抗という。
回路に流れる電流はi はで与えられる。
Rでの電力Pは
この式から,r=Rの場合にRでの電力が最大になり,最大電力はである。
18-7 キルヒホッフの法則(Kirchhoff's law)
① 第1法則 閉回路中の分岐点で,電流の代数和は0である。(入る電流と出て行く電流は等しい)
② 第2法則 任意の閉回路で,起電力の和=電圧降下の和
(閉回路に正の向きを決め,その向きの起電力,電圧降下を正とする)
第2法則で,(閉回路数-1)の数の式をたて,残った未知数だけ第1法則をたてる。
18-8 電力(power)
単位時間(1[s])に電気抵抗に流れる電流がする仕事を電力P[J/s=W]という。電気抵抗R[Ω]の電圧降下をV[V],電流をI[A]とすると,電力Pは
P=VI=I2R=V2/R (18-6)
で与えられ,抵抗で発生する熱量(ジュール熱)はPt=VIt=I2Rtである。
18-9 半導体(semi-conductor)とは
導体は抵抗率の温度係数が正だが,これが負である物質が半導体である。つまり,温度が上昇すると,導体は抵抗値が増加するが,半導体は抵抗値が減少する。
半導体の種類
(1) 真性半導体・・・ Si、Ge は、最外殻に4個の電子を持ち、これらの電子は共有結合をさせる働きをしており、自由電子にはならないので抵抗率が大きく電気を通しにくい。しかし、温度が上昇すると抵抗率が小さくなって電気を通しやすくなる。このような半導体を真性半導体という。
(2) 不純物半導体・・・真性半導体に微量の不純物をいれたもので、常温でも電気伝導性がある。
(a) n 型半導体 Si、Ge などの真性半導体に、5個の価電子をもっている15族の元素 P、As、Sbなど(これらをドナー[donor]と呼ぶ)を微量加えたもの。Si、Ge の原子は4個の価電子をもち、たがいに共有結合しているが、5個の価電子をもつ P、As、Sb の内の4個が共有結合に加わり、1個の価電子が余る。この余った価電子は結晶内を動きまわり、電流の担い手(キャリア)になる。n 型半導体のキャリアは電子である。
(b) p 型半導体 Si、Ge などの真性半導体に、3個の価電子をもっている13族の元素 B,Al、Inなど(これらをアクセプター[ acceptor ]と呼ぶ)を微量加えたもの。B,Al、In は価電子が 3 個であり、共有結合するのに電子が 1 個不足して電子のないところができる。これをホール(正孔)という。電場を与えるとホールよりエネルギーの高い共有結合の電子が移動してホールを埋め、電子が移った後が新しいホールになって別の電子がこれを埋める。このように、ホールは電場の向きに移動し、正の電荷の粒子のように振る舞う。p 型半導体のキャリアはホールである。
(3) ダイオード(diode)
ひとつの半導体結晶内に p 型の部分と n 型の部分を作り、それぞれに電極を取り付けたもので、p 型と n 型の接している部分を pn 接合という。ダイオードは整流作用、検波作用に利用される。
pn 接合部分では,n 型領域から p 型領域へ電子が拡散し,p 型領域から n 型領域へ正孔が拡散する。その結果,n 型領域には正イオンが,p 型領域には負イオンが残され,pn 接合部分にはキャリアが存在しない領域ができ、これを空乏層とよぶ。空乏層には,正イオンと負イオンによって,電子と正孔の拡散を妨げる向きに電場ができる。この電場によって生じる電位差を電位障壁という。
順方向と逆方向
順方向・・・ p 型部分が n 型より高電位になるように電池をつなぐと、接合面を通って p 型の中のホールは n 型へ、 n 型の中の電子は p 型に引かれ、このホールと電子は接合面で1対ずつ結合して消える(再結合)。p 型では正電極に引かれた電子のあとにホールができ、n 型では負電極から電子が送り込まれる。このように連続してキャリアができるので電流が流れる。
逆方向・・・ n 型が p 型より高電位になるように電池をつなぐと、ホールと電子はともに接合面から遠ざかる向きに力を受けて移動し、接合面付近にキャリアが存在しなくなり、電流がほとんど流れなくなる。
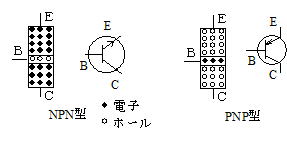
(4) トランジスター(transistor)
n 型と p 型半導体を図(a)のように組み合わせたものを npn 型トランジスター、図(b)のように組み合わせたものを pnp 型トランジスターという。E 電極はエミッター、B 電極はベース、C 電極はコレクターという。
エミッターとベース間に順方向の電圧をかけ、信号電流を流すと、エミッターとコレクターの間の電流が大きな変化になり、これを増幅作用という。

18-3 電気抵抗
問110 金属が導体であるのは金属内に伝導電子が存在するからである。これらの電子は様々な方向に運動しているが,電界が与えられると,全体として電界の方向に流れはじめる。
(1) 電子の電荷を-e,質量をmとして,強さEの電界によって生じる電子の運動を与える方程式をかけ。
(2) 電界によって加速された電子は,速度vに比例する抵抗力kv(kは比例定数)を受けて,やがて全体として等速度運動をすると考えてよい。
このときの速度を求めよ。
(3) いま,断面積S,長さlの銅線の両端に加えたある電位差のもとで定常電流が流れている。単位面積当たりn個の伝導電子が,比例定数kをもって速度vに比例する抵抗力を受けて等速度運動しているとして,この銅線の電気抵抗を求めよ。
18-4 合成抵抗
問111 図1,2,3において,a,b,c,d,e,f,g,h,i は端子を,I は直流電流を,Rは添え字の有無に関わらず抵抗を,それぞれ示している。I,Rのうち必要なものを用いて以下の問に答えよ。
(1) 図1において,直流電流I を端子aから流入させ,端子dから流出させる。このとき,端子bから端子cに向かって抵抗R0を流れる電流I0を求めよ。
(2) 図1のR0を取り外したとき,端子bc間の電位差Vbcを求めよ。
(3) 図1において,端子ad間の合成抵抗R1を求めよ。
(4) 図2において,直流電流I を端子aから流入させ,端子i から流出させるとする。このとき,(1)または(2)の結果を参考にすると,図2は図3のように表すことができる。このとき,それぞれの端子be間,de 間,ef 間,eh間の合成抵抗Rbe,,Rde,Ref,Rehを求めよ。
(5) 図2において,端子ai 間の合成抵抗R2を求めよ。
18-5 電流計・電圧計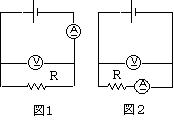
問112 内部抵抗が10Ωで,最大目盛りが10mAの電流計が2個ある。いま,その一方を最大目盛り10Vの電圧計Vとして使用し,他方を最大目盛り100mAの電流計として使用したい。
(1) そのためには,もとの電流計にそれぞれ何Ωの抵抗をどのように接続すればよいか。
(2) そのときの,電圧計Vおよび電流計Aの内部抵抗rVおよびrAを求めよ。
さて,この電圧計Vと電流計Aを電池に接続して,ある抵抗の抵抗値Rを測定しようと思う。その場合,図1および図2に示す2通りの接続が考えられる。しかし,いま,この2通りの接続について,電圧計Vの読みを電流計Aの読みで割って求めた抵抗値を,それぞれR1およびR2とすると,それらはいずれも正しいRの値を与えない。
(3) R1,R2およびRの大小関係を不等式で表せ。
18-7 キルヒホッフの法則
問113 図において,R1,R3,R4,R5はそれぞれ10[Ω],20[Ω],40[Ω],60[Ω]の抵抗,R2は0~20[Ω]に変化できる抵抗である。E1,E2はそれぞれ起電力が2[V],10[V]の内部抵抗の無視できる電池である。次の問いに答えよ。
(1) 図の回路を解くために必要な,電圧電流についての方程式を示せ。
(2) R2=15[Ω]としたとき,R1,R3,R4を流れる電流の大きさと向きを求めよ。また,このときAB間の電圧はいくらか。
(3) R3を流れる電流が0になるときのR2の値を求めよ。
18-8 電力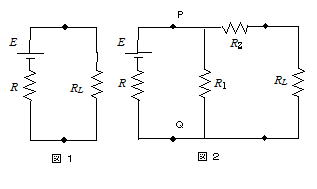
問114 図1は,起電力E,内部抵抗Rの直流電源に対して,負荷抵抗RLをつないだ回路である。
問1 図1において,RLに最大の電力を供給するためには,RLとRの間にどのような関係式が成り立たねばならないか。途中の過程も示せ。
なお,この関係式は見方を変えると,直流電源から最大の電力を取り出すための条件式でもある。
図2は,図1に対して,抵抗R1とR2を付け加えた回路であり,P,Qは端子を表している。
問2 PQの右側につながっている抵抗を1つの抵抗と見たとき,その値をR0とし,R0をR1,R2,RLを用いて表せ。
いま,図2において,RL=Rであるとしよう。このとき,RLの両端にかかる電圧はEのn分の1であり,しかも直流電源からは,最大の電力を取り出すことを条件として,R1とR2を,それぞれRを用いて表すことを,つぎの手順で考えよ。
問3 RLの両端にかかる電圧E/nをE,R1,R2,Rを用いて表せ。
問4 直流電源から最大の電力を取り出す条件を表す式と,問3で得られた式から,R1とR2を求め,それぞれnとRを用いて表せ。
ホーム メニュー 静電界 コンデンサー 直流回路 磁界 電磁誘導 交流