ホーム  メニュー            波動    波の性質    音波   ドップラー効果  弦振動気柱振動    光波の諸性質    幾何光学
                                                                               

【１３】波動
１３−１ 波動
  波とは

小石を静かな水面に投ずると波が広がっていく。このとき，水面に置かれた木の葉は波とともに移動することはなく，単に上下に振動している様子を見ることができる。波動はなんらかの振動源の振動が物質中を伝わっていく現象である。水面波での水のように波を伝える物質を媒質と呼ぶ。
         波が広がる様子を見る ⇒

　波の種類

波は伝わり方の違いから次のように分類される。
縦波(疎密波) 媒質内の各点の振動方向と波の進行方向が互いに平行な波(図参照)
　　　　例：音，地震波のＰ波(Primary Wave)
　　縦波は振動方向と波の進行方向が同じなので，そのまま図示できない。
     波の進行方向の変位を正，逆方向の変位を負として横波型で図示する。                                 パルス波 (媒質の振動方向 ⇔)
　　媒質中に疎(密度最小)，密(密度最大)ができるので，疎密波と呼ばれる。(下図参照)                      (マウスを載せると写真が動く)
                               
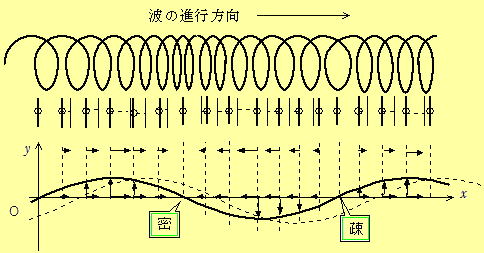
(上図の「密」と書いてある場所は，その左右が最も近づくので密度が最大になるので「密」と称し，「疎」と書いてある場所は，その左右が最も遠ざかる場所なので，最も密度が小さくなるので「疎」と称する)

横波 媒質内の各点の振動方向と波の進行方向が互いに垂直な波
　　 弾性体内に生ずる波の場合，縦波は媒質の体積に関する弾力が復元力になって生じ，
　　 横波は形に関する弾力が復元力となって生じる。            

　　例：光，電磁波，地震波のＳ波(Secondary Wave)
表面波 媒質の表面を伝わる波

例：水波，地震波のレイリー波(波の進行方向に平行な鉛直面内に振動する波)，ラブ波(波の進行方向に平行な水平面内に振動する波)。
これらは弾性体内部に起こった縦波横波が表面に達すると，媒質の弾性条件によって発生するもので，両者は殆ど等しい速度で表面に沿って伝わる。                                                                  

弾性波の速度 弾力が復元力になって弾性体内に生ずる波を弾性波という。

(1) 棒に沿った縦波 (E：のびの弾性率，ρ：密度)  
(2) 無限に広い固体内の縦波 (K：体積弾性率，G:ずれの弾性率)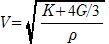   

    (体積弾性率については音波[空気中の音速についての歴史]参照)

(3) 流体内の縦波  
(4) 固体内の横波  
　　(流体ではG＝0だから，その中での横波の速度は0。だから流体中に横波は起こらない。)

水波  水波の復元力は重力と表面張力である。その速度Vは          水波の伝わり方を見る

(λ：波長，σ：水の表面張力，ρ：水の密度)
波長が長い場合(λ＞15cm)      (重力波という)
(波長が水深に比べ十分短い場合がこれにあたり，水の表面で円を描いて振動している)
波長が短い場合(λ＜5mm)    (表面張力波という。さざなみがこの例)
波長が水深に比べ十分大きい場合(遠浅の海岸など)  
   水面で横に平たい楕円を描き，水底では水平直線に沿って振動する。    (h：深さ)

波の方程式

左図は波の進む様子を示したものである。横軸は位置を示し，時間経過にともなう各点の変位を示す。この図から，時間経過とともに各位置は上下に往復運動し，これにともなって波が右方に伝わっていく様子がわかる。
  媒質が単振動しているとき，波は右下図のような正弦波になる。縦軸を媒質の変位として表すと，変位の正の最大値の位置を山，負の最大値の位置を谷と称する。また,同位相の位置の間隔を波長λ，変位0から最大値までを振幅Aと称する。媒質が１往復する時間を周期T (s)，振動数をf (Hz)とすると，
      の関係がある。
(単位Hz＝人名Herzによるが，単位の意味は回数/sで１秒間に繰り返される振動の回数を表す)
1周期の時間が経過すると，波は進行方向に１波長分進むので，波の速さvは
       [m/s]
で与えられる。

        波の方程式

波の変位を表す式は次のように表す。媒質の変位を y，位置座標を x，時刻を t，振幅を A とする。右下図のように横波が時刻 t＝0 で実線である場合を考える。波が図の右向きに進む場合，原点　x＝0　では次の瞬間　＋y　向きに動くから (点線波形に変わる)，原点の変位 y0 は
       
である。               (マウスを載せる)
位置　x　ではこの単振動が  [s] 遅れて伝わるから，
位置 x で時刻 t の変位 y は
             (13-1)
で与えられる。これを正弦波の方程式(または変位方程式)という。
　この式から x を指定するとある位置 x での単振動の式，t を指定するとある時刻の波形がわかる。  
  波が図の左向きに進む場合，原点はt＝0 の直後に下向きに動こうとするから，位置 x で時刻 t の変位 y は
           で与えられる。

                         (マウスを載せる)
式の中のを時刻 t，位置 x における位相という。位相がきまれば変位もきまる。一般的には正弦波の方程式は
            (13-2)
と表し，δ を原点の初期位相という。この場合，t＝0，x＝0 で y＝Asinδ となり， (13-2)式は(13-1)より δ だけ「位相が進んでいる」という。

例 (13-1)で示される正弦波があるものとするとき，波源から0.2[m]の地点の時刻 t [s] の変位y [m] が y＝0.3sin4π(t−0.5) で表される。この波の振幅,周期,振動数,速さ,波長を求めよ。

解 (13-1)と与式から
    振幅A＝0.3[m]，周期T＝0.5[s]，振動数f＝1/T＝2[Hz]，速さ v＝0.4[m/s]，波長λ＝v／f＝0.4／2＝0.2[m]
 

ホーム  メニュー            波動    波の性質    音波   ドップラー効果  弦振動気柱振動    光波の諸性質    幾何光学
           Top