ホーム メニュー ![]() 波動 波の性質 音波 ドップラー効果 弦振動気柱振動 光波の諸性質 幾何光学
波動 波の性質 音波 ドップラー効果 弦振動気柱振動 光波の諸性質 幾何光学
【14】音波と発音体
14−1 音の回折,反射,屈折
媒質を伝わる縦波を音という。
音も波だから反射,屈折,回折,干渉現象を示す。
音の特徴を表す物理量として3つの量,高さ(振動数),強さ,音色(波形)がある(音の3要素)。 音の波形を見る(人間の「あいうえお」とワイングラスなど)
高さ:人間に聞こえる音(可聴音)の範囲は20〜20000Hz(波長は1.7cm〜17m)である。コウモリ,イルカなどは20000Hz以上の音(超音波)を聞き取ることができる。
強さ:[波の強さ]参照
音の場合も,強さI は I ∝(f A)2,つまり振動数,振幅それぞれの自乗に比例する。強さの単位はJ/sm2=W(ワット)/m2である。
音の強さはデシベル(dB=deci Bel)とフォン(phon)で表す。
参考 ウェーバー・フェヒナーの法則によると
「振動数一定のとき,音の強さI の感覚はlog10I に比例する」
dB(デシベル)
ウェーバー・フェヒナーの法則をもとに,dBは次のように決められる。
たとえば,10-10J/m2・s の強さの場合,
なお,デシ(deci)は1/10を表し,ベル(Bel)は2つの電力P1 とP2 の電力比を対数表示した log(P1/P2) を表す単位である。
フォン(phon)
音から受ける刺激の大きさは,振動数によって異なる(右図参照)。
1000Hzで20μPa(マイクロパスカル)で0フォン,200μPaで20フォンとし,
1000Hzで測定したときと同じ音の大きさがα(dB)のとき,αフォンとする。
たとえば,人の会話は1mで60フォン,大声で100フォンである。
音速
静止乾燥空気中の音速v は,気温をt [℃]では
v=331.5+0.6t [m/s] (14-1)
で与えられが,次のようにして求められる。
定数kを用いると音速v は・・・・①
分子量をM,物質量n (mol)の気体体積をVとすると pV=nRT ・・・・・②,・・・・③
②③式よりこれを①に代入して
温度をt (゚C)とすると,音速vt は・・・・④
0゚Cのときの音速は331.5[m/s]だから
④/⑤から
vt ≒331.5×{1+t /(2×273)}=331.5(1+0.00183t)=331.5+0.61t (m/s)
(ただし,|x|≪1のとき,(1+x)n≒1+nx の 近似式を使った)
上記の音速は,静止乾燥空気中の音速だが,空気中に水蒸気がある場合,湿度補正が必要になる。
気温をt℃,気圧をP,そのときの水蒸気だけの分圧をP’とすると,空気だけの分圧はP−P’で空気の密度をρ,ρ1を空気の圧力をPに等温圧縮したときの密度とすると,
温度t,圧力P' の水蒸気の密度をρ2,ρ'を水蒸気の圧力をPに等温圧縮した場合の密度とすると,
経験則によると等圧Pでの水蒸気と空気の密度の比はρ'/ρ≒5/8なので,空気・水蒸気の混合気体の密度は
よって,湿度のある空気中の音速は
P '=0とすると,上記の乾燥空気での音速である。
![]()
空気中の音速についての歴史
(1) ニュートンの考え。(断熱変化として捉えなかった)
空気柱を想定し,そこに音波が伝わるとした。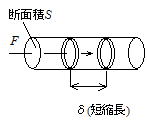
微小時間dt(s)に縮めた部分がdx 進むと,その速さvは![]()
また,その部分の運動量は(S ρδ)v であり,これが力積に等しいから
Fdt=(S ρδ)v ・・・・①
空気の体積弾性率(Bulk ModuLus)をkとすると,
![]() ・・・・② ∴
・・・・② ∴ ![]()
①,②式から
Fdt=![]() ・・・ 実際と合わない。失敗!
・・・ 実際と合わない。失敗!
(2) ラプラスの考え(空気振動を断熱変化と考えた)
断熱変化の式 ![]() をV について微分して
をV について微分して
![]() ∴
∴ ![]()
∴
![]() ・・・ ①
・・・ ①
ボイルシャルルの法則から ![]() これを①に代入して
これを①に代入して
![]() (
(![]() )
)
![]()
![]() 体積弾性率は,
体積弾性率は,
弾性体の表面に一様な圧力pを加えて単位体積当りε だけ圧縮したとき(ε は体積ひずみ),p/ε をいう。この逆数が圧縮率。多くの固体で体積弾性率は1010〜1011 N/m2
![]() 音速の壁を越えるジェット機の図 (NASAによる)
音速の壁を越えるジェット機の図 (NASAによる)
![]()
気体中の音速は圧力に依存しない。可聴音範囲では振動数に関係しない。振幅が多いとき,多原子分子では,物質に特定の振動数付近でγ が振動数とともに変わるので,速さは振動数とともに増加する。100MHz程度では,分子的吸収があり必ず音速は増大する。
| 固体 | 氷 | 3230 |
| 鉄 | 5130 | |
| 液体 | 水 | 1500 |
| エチレンアルコール | 1207 | |
| 気体 | 空気(0℃) | 331.5 |
| 空気(100℃) | 404.8 | |
| 水素(0℃) | 1269.5 |
固体,液体の音速を表す式は[13-1波動]参照のこと。
水の音速Vはt (℃)では
V=1403+5t−0.06t 2+0.0003t 3(m/s)
(海水中では塩分のため速くなり,常温で 1500m/s)
それぞれの現象の例
反射:やまびこ,鳴き竜(日光日光輪王寺薬師堂,京都相国寺法堂,甲府甲斐善光寺金堂いずれも竜の絵が描かれている))
屈折:冬の日没後などに遠くの音が聞こえやすい。上空で温度が高く,地表で温度が低いことが原因。
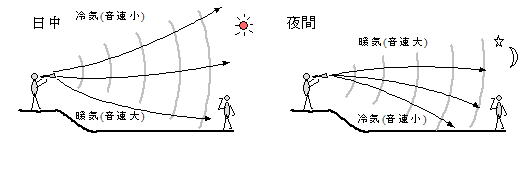
回折:塀の向こう側に音源をおいても,その音が聞こえる。姿が見えなくても音だけ回折するのは波長の違いによる。音の波長の方が光の波長より遙かに波長が長いためである。[13-2波の性質
回折 参照]
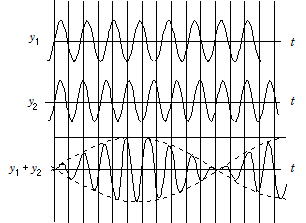
干渉:うなり(右図のように振動数の異なる(f1,f2とする)2つの音叉を同時に鳴らすと(それぞれの振幅はy1,y2),合成音はy=y1+y2になり,元の振動数にない強弱であるうなりが現れる。
下図で時間Tの間に振動数f1の音がn個, f2の音がn+1個あったとすると,それぞれの周期をT1,T2 とすると ![]() から
から
T=nT1=(n+1)T2 ∴ ![]()
∴ ![]() よって,
よって, ![]()
うなりの振動数f は f=| f1−f2| (14-2) である。 つまり,うなりの振動数は2つの振動数の大きさの差で与えられる。
うなりを聞こう(スピーカーのアイコンをクリックする)
(WindowsXP SP2でセキュリティ警告がでる場合、「開く」にして下さい)
400Hz の音 ![]()
400+401Hzのうなり ![]()
401Hzの音 ![]()
三角関数を使った定式化
うなりをそれぞれの波源からの変位の和として求める。
① うなり
それぞれの振動数が f1, f2 (f1>f2とする)の振幅A,速さv,波長が等しい波が互いに向かい合って干渉する場合,それぞれの変位が
とする。重ね合わせの原理により,合成波の変位 y は
←
f1≒ f2つまり,f1−f2≒0 の場合,(時間変動項)の1周期間に
(振幅項)が緩やかに変化する。これがうなりである。
特定の位置 x で(たとえばx=0) の1秒間中の最大(最小)の回数をうなりの回数という。
||が最大(最小)になる時間間隔 T は,x=0 では
π(f1−f2)T=π ∴
うなりの回数f は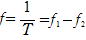
② 2次元の干渉(波源が同位相の場合)
S1P=l1,S2P=l2とする。
点Pでの振幅は
2A|| ∴ |
|=nπ ∴ |
|=nλ ・・・強め合う
||=(2n+1)
∴ |
|=
・・・弱め合う (n=0,±1,±2,±3,・・・)
クインケ管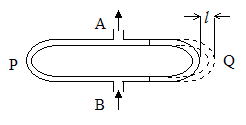
干渉現象を使って,音の速さ,波長などを測定するために使われる装置で右図のように,半分だけ管の長さが変えられ装置である。Bから音を送り出しAで音を聞く。Qをゆっくり引き出すと長さ l 毎に音が小さくなる。
はじめに音が打ち消し合うのはB→P→A経由の音(右下図 ①)の山とB→Q→A経由の音の谷aが干渉した結果である。Qを伸ばして次に音が打ち消し合うのは,B→Q→A経由の音の谷bが①の音と打ち消し合った結果である。これのことから,2l=λ から波長を求めることができる。
[波の性質] で考えた干渉条件と同じ形で表せば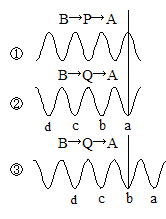
経路差⊿l=![]() が弱め合う条件である。
が弱め合う条件である。
干渉次数が1違う場合の経路差が2lだから,n=0で⊿l=![]() ,n=1で⊿l=
,n=1で⊿l=![]() だから
だから
2l=λ を得ることができる。
例 クインケ管を使って音の干渉を調べたら,管をl=8.5cm引き出す毎に音が小さくなった。
音速を340m/sとすると,音源の振動数f はいくらか。
解 2l=λ から,![]()
ホーム メニュー 波動 波の性質 音波 ドップラー効果 弦振動気柱振動 光波の諸性質 幾何光学
Top