�z�[�� ���j���[ ![]() �g�� �g�̐��� ���g �h�b�v���[���� ���U���C���U�� ���g�̏����� ���w
�g�� �g�̐��� ���g �h�b�v���[���� ���U���C���U�� ���g�̏����� ���w
�P�S�|�R ���U��
����U��������ƁC���[���߂ɂȂ����g���ł���B(�E�}�Ƀ}�E�X��u���Ɠ���ɂȂ�܂�)
���͂�T[N]�C�����x(�P�ʒ�������̎���)����(Kg/m)�C���̒�����l[m]�C����`��鉡�g�̑�����v[m/s]�C
���̐���m�C���ꂼ��̔{�U���ł̔g���� ��1�C��2�C��3,����C�U������f1�Cf2�Cf3,����Ƃ����
��{�U����l
�Q�{�U��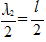
�R�{�U��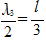
m�{�U����(m=1,2,3,���)
�����ŁCv�� ����`��鉡�g�̑����ŁC���̐����x����(Kg/m)�C���͂� S(N) �Ƃ�����ŗ^������̂�
�ŗL�U���� fm ��(14-6)
�ŗ^������B�܂�m�{�U���̔g����m���ł���B
�E�}�̇@�`�C�͊�{�U���C�Q�{�U���C�R�{�U���C�S�{�U���̒��g�ł���B
�{���͔g�����������狁�߂��邪�C���Z�ł͂��̎��͎g���Ȃ��̂ŋߎ����ċ��߂�(�݂͕Δ����L��)�B
����`��鉡�g�̑������ł��闝�R
(1) �^���������ɂ����@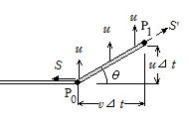
���̐��������ɓ������͂�S�Ƃ���B���ɗ�S ' ������(�����L�т���S���傫��)���Ƃ���ƁC���ɓ����͂̂荇������C
S 'cos���|S��0
�ߕ���P0P1�͏�����ɑ���u�œ����C�p���X�g������v�Ői�ނƁC����v��t �����̎��ʂ���v��t�ŁC���ꂪ������̉^���� (��v��t)u ������������B�^���ʕω��͉�����ꂽ�͐ςɓ���������
(��v��t)u��(S 'sin��)��t��Stan�����t��S()��t
����0�Ƃ����sin����tan���CS '��S�ƌ��Ȃ��邩��
(2) �g���~�^���̈ꕔ�ƍl������@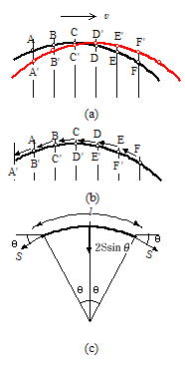
�}(a)�̉~�ʏ�̓_A�`F�̓������l����B���g���E���֑���v�Ői��ł���B�������Ԍo�߂����g�`��Î~�n�Ō���ƐԐ��Ɏ����悤��A��A'�CB��B '�CC��C'�Ɖ��ցCD��D '�CE��E '�CF��F '�Ə�֕ψʂ��Ă���B������C�E�֑���v(���)�œ����n�Ō���ƁC�}(b)�̂悤�ɓ_A�`F���~�ʂɉ�����A�f�`F�f�Ɉړ����Ă���悤�Ɍ�����B�܂�C�g���i�ނ��Ƃ�(�~�ʂƌ��Ȃ���)�g�Ɠ��������Ō���ƁC�}(c)�̂悤�ɂȂ�B
l��2r���̕��������ar�ʼn~�^�����Ă���ƍl����ƁC2r���̎��ʂ����2r���ŁC���S�͂�2Ssin���ƂȂ邩��C�^����������
���2r�����2Ssin��
����0�Ƃ����
���2r�����2S��� ��
(3) ������͂ŋ��߂���@ (������͂ɂ��Ắu�͊w�v�|[���_�����ʎ���]�Q��)
����`��鉡�g�̑���v�́C����S�C�����x���ŗ^����ꂩ�� v(S�C��)
�������� [v]��kS x�� y �� LT-1��(LMT-2)x (ML-1) y
���ӂ̎w�����ׂ�
L�ɂ��� 1��x�|y �CT�ɂ��� -1���|2x �� x���Cy��x�|1��
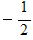
�������
(k��1�͂��̕��@�ł͋��߂��Ȃ�)
![]()
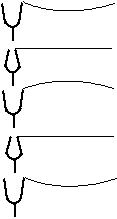 �g���̐U�������ƁC���̐U�������ɂ��Ⴂ
�g���̐U�������ƁC���̐U�������ɂ��Ⴂ
�g���ƌ��̐U�������������ꍇ�́C�U�����݂͌��ɓ��������C����炪��������ꍇ�͈Ⴄ���ʂɂȂ�B�}�̂悤�ɁC�g���Ƃ��ĉ������l����Ɖ����̐U�������ƌ��̐U���������قȂ�Ƃ��̎��ԕω��ɂȂ�B�܂艹�����Q�����������ԂɌ��͂P���������������ƂɂȂ�B���̌��ʉ����̐U����f1�ƌ��̐U����f2�̊Ԃɂ�
f1��2f2 �̊W������B
�Ⴆ�C���}�̂悤�ɒ����������U��(�����C���͓���)�̕��̐��� 2�F1�̊����ɂȂ�B
�P�S�|�S �C���U��
��
��[�������ǂ�ǂƂ����B�r�̌��𐁂����ꍇ�C�キ�������ꍇ�C�����������ꍇ�ʼn���ނ��̉����o���ėV�o���͒N�������邾�낤�B���N�M�̃L���b�v�̏ꍇ�������ł���B
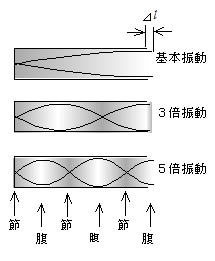
�J�[������˂������g���[�ŌŒ�[���˂��Ċ����āC�J�[�����C�[�͐߂ɂȂ�悤�Ȓ��g���Ł@����B�߂̈ʒu�͌��݂ɑa���ɂȂ�C���x�ω����ő�ł���B�J�����̕��͊J�[���班���o���ʒu�ɂ���C���̂�����J���[���l �Ƃ����B�ł��Ⴂ���g�̐U��������{�U�����Ƃ����B��[�����C���[���߂ɂȂ邩��{�U���͊�{���ɂȂ�B���̏ꍇ�Ɠ������@�ŁC�ǂ̒�����l �C���̐���n�C���ꂼ��̔{�U���ł̔g������1�C��2�C��3,����C�U������f1�Cf2�Cf3,����Ƃ�������ꂼ��̔{���̐U���������߂��
��{�U��
�R�{�U��
�T�{�U��
n �{�U����(14-7)
(n=1,2,3,���)
�������Cv�͋�C���̉����ł���B

�Ǔ��̉����͌����ɂ͎��R��C���̉������x���Ȃ�B
�~�ǂ̒��a�� d(cm)�C�����̐U������ f �Ƃ���ƁC�Ǔ��̉���V �͎��R��C���̉��� v �Ƃ���Ə퉷�ł́CV��v �ł���B
�J��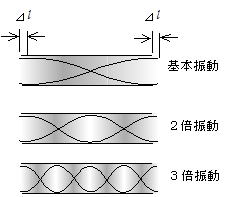
���[���J�����ǂ��J�ǂƂ����B��ʂ̊NJy��͊J�ǂł���B��[������˂������g�����[�Ŏ��R�[���˂��C�Ăь��̊J�[�Ŏ��R�[���˂��J��Ԃ������āC���[�����ɂȂ�悤�Ȓ��g���ł���B�߂͖��ɂȂ邱�ƁC���̕����͖��x���ł��傫���ω����邱�Ƃ͕ǂƓ����ł���B�g�����{�[�����v���o���Ă݂�Ε����邪�C�������ς��ƊJ�ǂƂ��Ē����ɉ��������̐U���������܂�B�Ƃ������Ƃ́C�J�[�͌Œ�[�̂悤�ɔ��˂���悤�Ȃ��̂��Ȃ��̂ɔ��˂���̂ł���B�����łȂ��ƒ����ɉ������U�������o�Ȃ����ƂɂȂ�B
�J���[���l �����[�ɂł���B�ŗL�U�����͊�{�U�����C2�C3�C����Ɛ����{�̐U�������ł���Bn�Ԗڂ̐U����fn�͉�����v�Ƃ��ĕǂƓ������@�ŐU���������߂��
�@�@�@(14-8) (n=1,2,3,���) �ł���B
�܂� �g�����ł���B
![]()
��L�̂悤�ɊJ�����Ŏ��R�[���˂��邱�Ƃɂ���ĊJ�ǂƂ��Ă̒��g���ł��邪�C�l�������o���ꍇ���������Ƃ��N�����Ă���B�܂�C���т�U�������Đ��������甭���Ă��邪�C�����Ɍ����琺�т����Ĕ��˔g������Ԃ���Ă���B�����甭�����������̂悤�Ȕ��˔g�����Ȃ����ĊO�Ɍ����悭����o�����߂̓�����K�z���ł���B���K�z���̌��͐l�Ԃ̌��Ɠ����傫���ŁC�O�C�ɐڂ��镔�����L�����ˉ����ŏ��ɂ��Ă���B���̃��K�z���̍L������́C���NJy��J�����̃A�T�K�I�Ɏ��Ă���B�A�T�K�I�̍L������͊y��̎�ނɂ���đ傫���قȂ�B�܂�C�t�����`�z�����C�X�[�U�z���Ȃǂ͊O���ɍs���قǑ傫���L����C�R���l�b�g�C�g�����{�[���Ȃǂ͂���قǂ̍L������ł͂Ȃ��B
�����́C�������ƊO�C�Ƃ̃C���s�[�_���X�}�b�`���O�̂��߂ƍl���邱�Ƃ��ł���B�𗬉�H�ł̃C���s�[�_���X�̃}�b�`���O�́C���͑��Əo�͑��̃C���s�[�_���X����v���Ă���ƃG�l���M�[���X���ŏ��ɂȂ�B���g�̏ꍇ������Ɠ����悤�Ȃ��Ƃ��W���Ă���B
�J���[��� l �̋��ߕ�
�E�}�̂悤�ȋC�������u�ʼn������nj����Ŗ炵��{�U���C�R�{�U���ŋ�������B�C���̒��������ꂼ��l1�Cl2�Ƃ���ƁC ����2(l2�|l1)������
(14-9) �ł���B
������O���t�����}�̂悤�ȃO���t��`���ċ��߂邱�Ƃ��ł���B
�J���[��́C�ǂ̔��a�C�U�����C�ǂ̌`��A�J�����̖ʐςɂ���ĈقȂ邱�Ƃ��m���Ă���B
�J�����ɕ������Ȃ��ꍇ��l�͓����a��r�Ƃ����0.6r�C�����ɍL������������ꍇ(�L���ǂɎ��t����ꂽ�悤�ȏꍇ)0.85r(��)�ł��邱�Ƃ��m���Ă���B ( �J���[��̎������ʗ�(���ar��1.53cm�̉~�`�f�� )
13-1 �g�� �g�̕�����
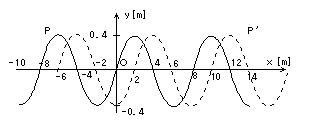 ��93 ����x���ɉ����Ēu����Ă���Bx����̈�_O�����_�Ƃ��C�E���𐳂̌����Ƃ���Bx���ɐ�����y�������͌��̉��U���̕ψʂ�\���B���̍��[�ɐU��������������C�������̐U���Ŏ����I�ɐU��������Ɣg��x���̐��̌����ɓ`������B�g�͐����g�Ƃ��Ĉȉ��̖₢�ɓ�����B
��93 ����x���ɉ����Ēu����Ă���Bx����̈�_O�����_�Ƃ��C�E���𐳂̌����Ƃ���Bx���ɐ�����y�������͌��̉��U���̕ψʂ�\���B���̍��[�ɐU��������������C�������̐U���Ŏ����I�ɐU��������Ɣg��x���̐��̌����ɓ`������B�g�͐����g�Ƃ��Ĉȉ��̖₢�ɓ�����B
����`���g�́C����t��0[s]�ł͉E�}�̎����̂悤�Ȕg�`���������B�܂�,����t��0.9[s]�ł͔j���Ŏ����悤�Ȕg�`�ɂȂ��āC���̊ԂɁC�g�̎R�o�͎RP' �ɐi�B
(a) ���̔g�́@(�)�g���@(�)�����@(�)����`���g�̑��������߂�B
(b) �����Ŏ����g�̌��_O����E��x[m]���ꂽ�_�̕ψ�y[m]��t ��x �̊��Ƃ��ĕ\���B�������C(a)�ŋ��߂����l�Ȃǂ�p����B
13-2 �g�̐��� ���g
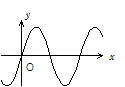 ��94 ���̕����m�@�n�̂Ƃ���ɓK�������܂��͎��������B�ψʂ��g���Ƃ��ā{x�����ɁC����V �Ői��ł���B����t���O�̂Ƃ��C�g�̌`��
��94 ���̕����m�@�n�̂Ƃ���ɓK�������܂��͎��������B�ψʂ��g���Ƃ��ā{x�����ɁC����V �Ői��ł���B����t���O�̂Ƃ��C�g�̌`�� ![]() �����@ �ŕ\�킳���Ȃ�C����͐����g�ł���C�퐔���͔g����\���B���̔g�̔C�ӂ̎���t�ɂ����鎮�����߂�ɂ́C���_�O�� Vt �����E�ɂ��炵�����W�ŕ\���·@�Ɠ����`�ƂȂ邱�Ƃ���
�����@ �ŕ\�킳���Ȃ�C����͐����g�ł���C�퐔���͔g����\���B���̔g�̔C�ӂ̎���t�ɂ����鎮�����߂�ɂ́C���_�O�� Vt �����E�ɂ��炵�����W�ŕ\���·@�Ɠ����`�ƂȂ邱�Ƃ��� ![]() ����A
����A
�Ƃ���悢�B�A�ŔC�ӂ̓_x�ɒ��ڂ���ƁC���̓_�ł� �͐U��a�Łi���j�m�@�n�U�����s���C���̐U�����͇A����(���j�m�@�n�ƂȂ�
���ɇ@�Ɠ����`�̔g���|x�����ɓ��������Ői��ł���Ƃ��́C���̔g�̔C�ӂ̎���t �ɂ����鎮��![]() ����B
����B
�Ə������Ƃ��ł��顂����Ƀ͂���퐔�ł��顂����A�ƇB�ŕ\�����Q�̔g�������}���̒��ɂ����āC�d�ˍ����̌��������藧�Ƃ���C�����g��
�@�@![]() �����C
�����C
�Ə����顂���͐i�s�g�ł͂Ȃ��i���j�m�@�n�Ƃ�������̂ł��顂���̐U���͏ꏊ�ɂ��قȂ�C�U��������0�ł���_�͇C����i���j�m�@�n��n(n��0�C1�C2�C�c���狁�߂��顂����̓_��(��)�m�@�n�Ƃ�����܂��U���������ő��2a�ł���_��(h)��2n�{�P�Cn��0�C1�C2�C�������狁�߂���B
14-1 ���̉�܁A���ˁA����
��95 �����c�g�ł��邱�Ƃ��������B
��96 x���̐��̌����ɐi��ł���c�g���Cx���ɐ����Ō��_�n��ɂ���ł��ǂɓ��˂��Ă���B�}�́C�ʒux�ɂ�����}���̕ψʂ�y���ɏ����\�����Ƃɂ��C���鎞���̓��˔g�̔g�`��`�������̂ł���(�_���͕⏕�̂��߂̂��̂ł���)�B���˔g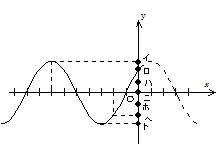 �̐U����A�C������v�Ƃ���Ƃ��C���̏c�g�͎���t�ɂ�����
�̐U����A�C������v�Ƃ���Ƃ��C���̏c�g�͎���t�ɂ�����
![]() �Ə������Ƃ��ł���B�}�ɂ�����x���̂P�ڐ���͂P[m]�ł���B
�Ə������Ƃ��ł���B�}�ɂ�����x���̂P�ڐ���͂P[m]�ł���B
(1) ���̓��˔g�̐U�����͂����炩�B
(2) ���˔g�̑���v �̒l�͂����炩�B
(3) �}�̓��˔g�ɂ�����,�}���̖��x���ő�ɂȂ��Ă���n�_�C����є}���̐U�����鑬�����O�ɂȂ�_��,���ꂼ�ꂱ�̔g�`�̂ǂ����B��������C�}�́|9��x��0 �͈̔͂ł�����x���W�����ׂĂ�����B
14-2 �h�b�v���[����
��97 ���̃h�b�v���[����
�������O�ɂ����āC���̐U�����̉������C�����̕ǂɌ������Đ����ȕ���������̑������߂Â��Ă���B��������o�ĕǂɐ����ɓ����������g�̓��C���̑啔���͐����ɔ��˂��C�킸���̕�����������ς��邱�ƂȂ��ǂ�ʂ��čL���Ēg�������O�ɐi�ށB�܂���������́C���̐i�s�����ɑ��Ĕ��̕����ɂ����g���o�Ă���B�����l�̉��g�̂����C�ǂɌ������Đ����ɐi�މ��g�̔g���́C�Î~�����l���猩������ł���B�����̑�����u�C���O����щ����ɂ����鉹�g�̑��������ꂼ��v1�Cv2�Ƃ��āC�����̉��g�̐Î~�����l���猩���g���ɂ��ē�����B�������Cv1��u�Cv2��u�ł���B
(1) �ǂŔ��˂������g�̔g���͂����炩�B
(2) ���O��i�މ��g�̔g���͂����炩�B
(3) �����̐i�s�����ɑ��Ĕ��̕����ɉ�������o�Ă������g�̔g���͂����炩�B
14-3 ���U��
��98 �E�}�̂悤�ɁCx��L���Œ�[�ŁCx��L�̔}�����𑬂�v�C�U����f�̐����g�̉��g��x���̐��̕�����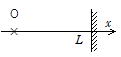 �i�s���Ă��āCx��0�ł̔}���̕ψʂ�
�i�s���Ă��āCx��0�ł̔}���̕ψʂ�
y1�i0�Ct�j��Asin2��f t�ł���B���̔g�̈ʒux�C����t�ɂ�����ψʂ�y1�ix�Ct�j�� (1) �ł���Bx��L�Ŕ��˔g��������Ɣ}�����ɂ͓��˔g�Ɣ��˔g�������ɑ��݂��C���̂Ƃ��̍����g�̕ψʂ� (2) �����ɂ���Ă��̂��̂̔g�̕ψʂ̘a�ɂȂ�B���˔g��x��L�ł̕ψʂ�y1�iL�Ct�j�� (3) �ł���C�Œ�[x��L�ł͔C�ӂ̎����ɂ����č����g�̕ψʂ�0�ɂȂ��Ă��Ȃ���Ȃ�Ȃ����Ƃ���Cx��L�ł̔��˔g�̕ψʂ�y2�iL�Ct�j�� (4) �ł���C�Œ�[�ł̔g�̈ʑ��̕ω��� (5) �ł��邱�Ƃ������Ă���B���˔g�͑���v��x���̕��̕����ɐi�s���Cx��L�ł̕ψʂ��ʒux�ɂ���Ă���̂Ɏ��� (6) ����������邱�Ƃ���C���˔g�̈ʒux�C����t �ł̕ψʂ�y2�ix�Ct�j�� (7) �ƂȂ�B���������āC�ʒux�C����t �ł̍����g��y�ix�Ct�j��2Acos2��f�it�|L/v�j�~ (8) �ł���B
�@����x��0���Œ�[�Ƃ���ƁC��̍l�@����C�U�����͐��̐���m��p����fm�� (9) �ƂȂ�B
�z�[�� ���j���[ �g�� �g�̐��� ���g �h�b�v���[���� ���U���C���U�� ���g�̏����� ���w
Top