�z�[�� ���j���[ ![]() �g�� �g�̐��� ���g �h�b�v���[���� ���U���C���U�� ���g�̏����� ���w
�g�� �g�̐��� ���g �h�b�v���[���� ���U���C���U�� ���g�̏����� ���w
�y�P�T�z���g
���Ƃ́C���O���C�������C�ԊO���CX���C�� �����܂߂��d���g���������C���`�ɂ͉������ł���g��380�`810nm�̓d���g�������B
����
�K�����I(1607�N) �����̗L�����ւ̒���B
�Â����� ���̑����͖����ɑ傫�����̂Ɛ����o������M�����Ă������Ƃɋ^��������C�����u�ԓI�ɓ`�����̂ł͂Ȃ��낤�Ƃ������Ƃ��C���d�̍ہC �������ꂽ�_�̊Ԃɓ`���d���̗l�q����\�z���Ă����B�����ŁC�����`���̂Ɏ��Ԃ�v���邩�ۂ��̎��������݂��B���[�}�[(Reomer1676�N)(1675�N�̐�������) �����Əڂ���
�K�����I�̒������u�V�Ȋw�Θb�v�̒��ŁC�u��C���������� 2�l�̐lA�CB���C1�`2km ����Č����������ė��B���߁CA�C B�Ƃ��Ɏ����̓�����ʼnB���Ă����B���ɁCA��B�̕������Ȃ���C�����f���������CB�Ɍ��𑗂�BB��A�̌���F�߂�ƁC���˓I�Ɏ���痣���CA�Ɍ����Č���Ԃ��BA�͌��𑗂��Ă���CB�̌���F�߂�܂ł̎��Ԃ��ώ@����B�����āCAB �Ԃ̋�����2�`3km �ɉ������āC�������Ƃ�����Ԃ��B�����`���̂Ɏ��Ԃ�v����Ȃ�C�����������������ʂ������͂��ł���v�B�Ƃ����B�������C���̎��Ԃ�l�̒m�o�łƂ炦��ɂ͒Z�����Ă��̎��݂͎��s�ɏI������B���݂ɁC1Km�������`���̂ɖ�3�~10-9�b������l�Ԃ̊��o�ő��肷�邱�Ƃ͏��F���������C�������L������������Ȃ��Ƃ������Ƃɒ��킵�����Ƃɂ͈Ӌ`������B
�n��̌�����p���������̑���ɏ��߂Đ��������B���Ԃ���]�����C���̌��Ԃ���̌������ł̔��ˌ����������鎞�ԂƎ��Ԃ̉�]���̊W��������𑪒肵���B�t�[�R�[(J.Foucault 1862�N) �����Əڂ���
�č����ۓx�ʍt�ψ���̃C�x���\�������艻�������[�U�[���̎��g��(���q���v�ƑΔ�)�Ɣg��(����p����)�����肵�����𑪒�B�@�@2.99792458�~108m/s�Ƃ��������x�̒l���B1983�N���ۓx�ʍt����̓C�x���\���̌��ʂ���Ɂu�����^��1/299792458�b�Ԃɐi�ދ�����1���[�g���Ƃ���v���̑����ꂽ�B���̂��Ƃɂ���ď]����Kr86��p������`���p�~���ꂽ�B
���ˁC���ˁC���܌��͋��E�ʂɐ����ȓ��ꕽ�ʓ��ɂ���B
���܂̖@��
�u���܌��͓��˖ʓ��ɂ���C�@���Ɋւ��ē��ˌ��Ɣ��Α��ɂ���v
�u���ˊp��1�Ƌ��܊p��2�̊Ԃɂ� n12���̊W������v�B������X�l���̖@���Ƃ����B
n12��}���Q�̔}���P�ɑ��鑊���ܗ�(relative refractive index) �Ƃ����B
�}���P�C�Q�̋��ܗ��C�����C�g�������ꂼ��n1�Cn2�Cc1�Cc2�C��1�C��2�ł�����ˊp����1�C���܊p����2�Ƃ���ƁC�}���Q�̔}���P�ɑ�����ܗ�n12��
�@�@�@�@(15-1) �ł���B
����� n1�Esin��1��n2�Esin��2(���ܗ� n�~sin�� �����)
�܂�C���ꂼ��̔}���ɂ���n�Esin�������ł���B
�^��ɑ�����ܗ������ܗ�(absolute refractive index)�Ƃ����B�w�肪�Ȃ��ꍇ�C���ܗ��͐���ܗ��������B
[��]
�E�}�̂悤�ɋ��܌������ˌ��̉������������ɋ��܂���̂� c1��c2�̏ꍇ(�Ⴆ��C���琅�ɐi�ޏꍇ)�ł���B
�^�琅�ɐi�ޏꍇ�ł����̏ꍇc1��c2 ������O���ɋ��܂���B
�}���P�C�Q�C�R�̐���ܗ���n1�Cn2�Cn3�C������c1�Cc2�Cc3�C���ˁC���܊p�����ꂼ����1�C��2�C��3�C��4�Ƃ���ƁC�}���Q�̔}���P�ɑ�����ܗ�n12�C�}���R�̔}���Q�ɑ�����ܗ�n23�C�}���S�̔}���R�ɑ�����ܗ�n34��
�ł���B�}���S���}���P�Ɠ����ꍇ�C��4����1�ɂȂ�B�܂�}���S�Ɣ}���P�̌��͕��s�ɂȂ�B
����P ���ܗ�2�̔}���ł̌����C�g���͐^��̉��{���B
����Q n12��n21�W�́B
����R �K���X�̋��ܗ���3/2�C���̋��ܗ���4/3�Ƃ���ƁC�K���X�̐��ɑ�����ܗ��͂����炩�B
�m���n ����P �Ƃ���1/2�{ ����Q n12��1/n21 ����R n(�K���X)�^n(��)��(3/2)/(4/3) = 9/8 (���̕�������)
![]()
�t�F���}�[�̌���
���̒��i�C���ˁC���܂�������邱�Ƃ̂ł��錴���B1658�N�t�F���}�[���l�������̂ŁC
�w��������_����ʂ̓_�ɐi�ނƂ��ɁC�Q�_�Ԃ̌��w�������ŒZ�ɂȂ�悤�ȓ���i�ށx�Ƃ������́B
���̌�C�u���w�������Ɍ����Ƃ�v�ƏC�����ꂽ�B
����P��O��Q�ƒʉ߂��鏊�v����t ��
���}�̂悤��a�Cb�Cc�Cx �����ꂼ��̒����Ƃ����
����
��
( ��)
����
�}���P�Ɋp�x��1�œ��˂������͊p�x��1�Ŕ��˂���B
���˂̖@�� �u���ˊp�Ɣ��ˊp�͓������C���ˌ����͖@���Ɋւ��ē��ˌ��Ɣ��Α��ɂ���v
�܂�C���͋��E�ʂŔ��˂���ƂƂ��ɋ��܂�����B
���ˁC���܂Ɋւ��鏔����
�@ �S����
c1��c2�̏ꍇ�C�}���Q����}���P�Ɍ�����˂�����B���ˊp��2��傫�����Ă����Ƌ��܊p��1���傫���Ȃ�C������ˊp��0�ȏ�ɂȂ�Ɣ}���P�ɋ��܂ł��Ȃ��Ȃ�C���ˌ������ɂȂ�B���̌��E�̊p�x��0���ՊE�p�Ƃ����C���̌��ۂ��S�����Ƃ����B�S���˂��N����̂͌������������}������������傫���}���ɐi�ޏꍇ�݂̂ł���(�Ⴆ�ΐ������C�ɐi�ޏꍇ)�B���t�@�C�o�[(��w�p�C�ʐM�p)�ȂǂɎg���Ă���B

��1 �E�}�ŁC�}���P�C�Q�̋��ܗ������ꂼ��n1�Cn2���ˊp����2�C���܊p����1�Ƃ��Ĕ}���Q����}���P�Ɍ����i�ޏꍇ���l����B��2����0(�ՊE�p)�̂Ƃ�����1��90߂ɂȂ�S���˂��N���邩��
�}���Q�̔}���P�ɑ�����ܗ���n12��(15-2)
�}���P����C(n1��1.000293��1�Ƃ���) �C�}���Q�𐅂̏ꍇ(n2��4/3) sin��0��3/4��0.75 �� ��0��49�x
��Q �E�}�̂悤�ɋ��ܗ����̕�����AB�ʂɌ������˂�
BC�ʂőS���˂����B���ˊpi�͉��x�ȉ����B
�S���˂̏�����sini 0���� i ��45�
�}��� r��30߂�����C
n����
����� i ��45�
�A �ʑ��ω�(phase difference)
�����g�������������ۂ̒��ŁC���w�I�ɑa�Ȕ}��(���܂�������)������w�I�ɖ�(���܂��傫��)�ɐi�ނƂ��̔��˂̏ꍇ�����ʑ�����(rad)�ω�����B���ł͕ω����Ȃ��B����́C��q�̔����C�������сC�j���[�g�������O�̊��̏��������߂邱�ƂɊW����B
���@������C���琅�ɐi�ޏꍇ�̔����@
�B ���H��(���w����)(optical path)
����l �̋�����^�Ŕg����0 �̌����i�ޏꍇ�C���̊Ԃ̔g����l/��0�C���ܗ�n�̔}�����ł�
�ƂȂ�B�܂�C���ܗ�n�̔}�����̔g�̐��͐^��̏ꍇ��n�{�ł���B
���̐^�̒����ɒu�����������������H�� (���w����)�Ƃ����B
���ܗ�n �̔}�����̌��H���͐^���n �{�ł���
�C �����オ�茻��
(a) �E�}�̂悤�ɔ}���Q���̐[��h�ɂ��镨�̂���C(�}���P)�����猩���ꍇ
�^�ォ�猩���ꍇ( i�C r��0 )
���̏ꍇ n12��4/3 �Ƃ����
r��0�łȂ��ꍇ
OQ�� htan r��h' tan i
��
�߂��猩���ꍇ
�E�}�̊p�x�����Ƃ��C��������̈ʒu��P'�Ƃ���Ɛ}�� x�C y��
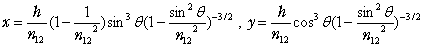
�ŗ^������B
(b) �}���Q�����C���̕��̂�^�����猩���ꍇ
(a) �̋t���l����������� h'��n12h
�Ⴆ�C�����ɂ��鋛����C���̐g���Pm�̎q����^�����猩�グ���
�@�@�@���� 1.3m�Ɍ��Ă��邱�ƂɂȂ�B
(c) �K���X�Ȃǂ��r���ɂ���ꍇ
��C���ɒu���ꂽ���ܗ�n �̃K���X�̉����̕���P�Ɍ������ď㑤����i��ł�������
�� PP'��BD��BC�|CD���܂�CP'��P��艓���Ȃ�B
�D �v���Y��
���p���̃v���Y���̈��AB�Ɍ������ˊpi �œ��˂����܊pi' �Ŗ�AC������܂���Ƃ� i��i' �Cr��r'�̂Ƃ��Ίp��(���ˌ��Ƌ��܌��̂Ȃ��p�x�B�E�}�Q��)���ŏ��ɂȂ�B
�E�}��� ����(i�|r)�{(i'�|r')��(i�{i')�|(r�{r')��(i�{i')�|��
�@�@�@ r �{r'���� ��� (a) ����i �{i'�|�� ��� (b)
���ܗ��̖@������
�@�@�@ sini��nsinr ��� (c) sini'��nsinr' ��� (d)
i�C����0�̏ꍇ (c)�C(d)�� i��nr �Ci'��nr' �����Ȃ����Ƃ��ł���̂ŁC�����(b)�ɑ������
�ŏ��Ίp�� ����n(r�{r')�|(r�{r')����(n�|1)
i�Cr��0�̏ꍇ i��i'��i0�Cr��r'��r0�C���̂Ƃ�������0�Ƃ����
(a)����2r0���� �� r0����/2�C(b)���� ��0��2i0�|��
����������0�Ƃ��ċߎ�����Ə�L�Ɠ������ʂɂȂ�B
����0�łȂ��ꍇ
(b)�������͈��l����������i �̊�������Ci �̂���l�ɑ��������ŏ��l�ɂȂ�̂�
���(e)
(a)������� (f)
(c)������� (g)
(d)������� (h)
(e)(g)(h)��(f)�ɑ������
r��r' (r��0�s�K) �� i��i'
���˗��Ƌz����
���̂Ɍ������˂���Ƃ��̊�����
���˗��ρ���1�ƒ�߂�B
�}�����Ƃ��ɓ����ȓ����̂̏ꍇ�̔��˗���
�����ɓ��˂���ꍇ��
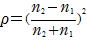
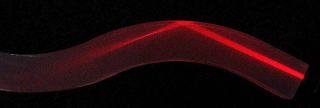
�E�}�ɋ�C����̌����K���X�Ŕ��˂���ꍇ�̗�������B
��ʂɋ����̃ς͑傫���C�����������ł̓ς͓��ˌ��̔g���Ɉˑ����Ȃ��B�\�ʂ����L�̐F��悷������ł͂��̐F���̔��˗������ɑ傫���B
���̗�(�������˂̏ꍇ) 3800�� 8100�� �� 44.5% 98.2% �� 37.8% 97.7% �� 92.8% 98.6% ���Ƴ� 92.5% 86.3%
�� �g�����傫���ƐԂ�������
�� �g���ɂ�炸����������
�z������ ���܌��̋����͔}���̋z���̂��ߎ�߂���B
���E�ʂɓ��˒���C����x ���ꂼ��̋�������t0�C��tx �Ƃ����
��tx����t0e - ��x(Beer�̖@��)
���͋z���W��(�g���ɂ��萔)
�z����a ��(a��1)
�@�@���ߗ��с�(��tr�͓��ߌ����x�C��0�͓��ˌ����x) �ρ{a�{�с�1�ł���B
�P�T�|�Q ��ܥ����(diffraction�Einterference)
![]() ��܂�1665�N�O���}���f�B�ɂ���Ĕ������ꂽ
��܂�1665�N�O���}���f�B�ɂ���Ĕ������ꂽ
������Q���̔w��܂ʼn�荞�݁C���w�I�ɂ͉A�e�ƂȂ�Ƃ���܂ŒB���錻�ۂ����̉�܂ł���B��܂͔g���������قNjN����₷���B�����ƃX�N���[������Q������L���̋����ɂ���Ƃ��鈵����Fresnel����܁C�\�������ɂ��邩�����Y�ŏW������悤�Ɉ����ꍇ��Fraunhofer����܂Ƃ����BFresnel���͐ϕ����g���v�Z�����G�Ȃ̂ō��Z�ł�Fraunhofer����܂������B
(�P) �����O�̊�����
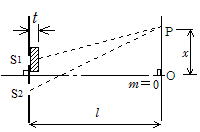
�����O��1807�N�ɍs���������g�ł��邱�Ƃ��ؖ���������ŁA�}�悤�ȕ��X���b�gS1�CS2�ƃX�N���[����̈�_�o�̋��������ꂼ�� l1�Cl2�C������̓_�n�Ƃo�Ƃ̋�����x�C�܂�S1�CS2�ƌ����̋��������ꂼ�� d/2�C���X���b�g�ƃX�N���[���̋�����l �Ƃ���B�`�a�ł̌������ʑ��Ȃ�
������ |l1�|l2|��m��
���� |l1�|l2|��(2m�{1)�@(m��0�C�}1�C�}2�C�}3��� ) (15-3)
�ŃX�N���[����ɖ��Â������B���������F�����̏ꍇ�͐F�̂������ÂɂȂ�B
�@ ���Ï�����l�Cd �Cx ���g���ĕ\���ƈȉ��̒ʂ�B
��
�̏ꍇ�C
2��L2�{(x�{
)2 �C
2��L2�{(x�|
)2
2�|
2��2d x ��
�|
��
(l��d �Ƃ��ċߎ�����B�����Fraunhofer���̈����Ƃ���)
����
�~ 2m (����)
��
�~(2m+1) (�Ð�) (m��0�C1�C2�C3�C��� m���������Ƃ���)
O�_����̋��� x�ŕ\���ƁCx��(����)�@�Cx��
�@(��)
��������1�قȂ�ꍇ��x�����Ȃ̊Ԋu��x������ ��x��
���̎�����C���̔g���̑��肪�\�ł���B���̂悤�ɁC�X�N���[����ɖ��Â̎Ȃ�����邱�Ƃ́C�����g���ł��邱�Ƃ��ؖ�������̂ł���B
��x�����番���邱�Ƃ́C
(a)�@l�Cd�����̏ꍇ�C��x �����͔��̊W������X�N���[���̌����ォ�牓�����ɔg���̒����ԁC�߂����Ɏ��F�����Ԃ��Ƃ�������B
�P�F�����̏ꍇ(He-Ne���[�U�[��) ���F�����̏ꍇ
������͂�����g���̌����d�Ȃ�̂ŁC���F(�F�����Ȃ�)�ɂȂ�B�P�F�����̏ꍇ�́C���Â�����邾���ł���B
(b) d�C�������̏ꍇ�C��x��l �͔�Ⴗ��̂ŃX�N���[���������Ȃ�قǁC��x �͑傫���Ȃ�B
(c) l�C�������̏ꍇ�C��x��d �͔����̊W������C���X���b�g��d ��傫������Ƈ�x �͏������Ȃ�Bd ���\���傫���Ȃ�Ɗ��Ȃ͌����Ȃ��Ȃ�B
��x ���̎��ɂ́C�P�X���b�gS�̕����ϐ��Ƃ��ĊW���ĂȂ��B
�P�X���b�g�̕���a �Ƃ���ƁC�X�N���[����̋��xI �� ���X���b�g����̊p�x�����Ƃ���Ƌ��xI�ŗ^������B
�@�������C�ł���B
sin�̂��������C���X���b�g���\������X���b�g�̕��ɂ�鋭�x�Ccos�ɂ����������X���b�g�ɂ�鋭�x�ł���B���̗������d�ˍ��킳��Ď��ۂ̊��͗l�� �Ȃ�B���X���b�g�̕Е������ǂ��ƑO�҂ɂ�銱�͗l��������Ȃ��B
�A �P�X�N���[��S�͂Ȃ��K�v��
���F������p�����ꍇS���Ȃ��ƃX�N���[����ɖ��m�Ȋ��Ȃ͌���Ȃ��B�P�X���b�gS�́C���̈ʑ������낦�邽�߁C�܂�C���������ɂ��邽�߂ɕK�v�����C���[�U�[�����̂悤�Ȉʑ��̂�����Ă�������̏ꍇ�͕s�v�ł���B���̂悤�Ȍ�������(coherent)�̌��Ƃ���(�u�g�̐����v13-3���œ��ʑ��̏������K�v�Ȃ��ƂƓ����ł���)�B�}�̂悤�ɒP�X���b�g�̕���a�C�P�X���b�g�ƕ��X���b�g�̋�����b�C���X���b�g����d �Ƃ���������Ȃ����ĂɌ���������ł���B
S�̈ʒu�����炷�ƁC���Ȃ͂ǂ��ω����邩�B
(�P)�̃����O�̊������̐}�ɂ����āC�P�X���b�gS�����y �ړ��������Ƃ��ɁC�X�N���[����̖������Ð��ɕς�����ꍇ�C�P�X���b�gS�ƕ��X���b�g�̋����� L�Ƃ���ƁC
�@�@�@�@������C
�ł���B
�B ���X���b�g�ƃX�N���[���Ԃɋ��ܗ�n�̕��������ƁC�Ȗ͗l�͂ǂ��Ȃ邩
�@ �� ��x������l�Cd ���Ƃ���Ɣg��������/n�ɕω�����̂ŁC
�܂�^��̏ꍇ��
�{�ɂȂ�B
���̂��Ƃ���C���X���b�g�ƃX�N���[���Ԃɋ��ܗ�n �̕����������Ƃ��̊��Ȃ̂��ꇙx ����C�������������̋��ܗ��𑪒肷�邱�Ƃ��ł���B
�CS1�����ɋ��ܗ�n�C����t �̕�����u�����ꍇ�C�Ȗ͗l�ɂǂ��Ȃ邩
���ܗ�n �̕������̌��w�����͐^��̏ꍇ��n �{�ɂȂ�(�u���ˁC���܂Ɋւ��鏔���ہv�B�Q��) �̂ŁC���X���b�gS1�CS2����X�N���[����̔C�ӂ̓_P�܂ł̌��w������
m�Ԗڂ̖����ōl�����
�@ �� xm'����
�{
�� ��x��
�|
��
n��1�����燙x��0 �܂� ���ܗ�n �̕�����u�������ɖ��Â̎Ȃ����s�ړ����邱�Ƃ��킩��B���̂��Ƃ���C�����̋��ܗ��𑪒�ł���B
�D �X�N���[������������Ɗ��Ȃ͂ǂ��ω����邩
d�C�������̏ꍇ�C����������m�ł͂ǂ̂悤�ɕω����邩�B
�� �@���疾���������ʒu�� x��
������Cx �� l �͔�Ⴗ�邩��C�X�N���[���̈ړ�������L�Ƃ���ƁCL��l �ł�2x�CL��2l �� 3x �ɂȂ邱�Ƃ��킩��B
d�C�������ŃX�N���[�������������ꍇ�C����x�ł́C�Â��Ȃ��Ă���Ăі��邭�Ȃ�C���銱����m�̖��������̖����ɕς��B���̂Ƃ��C�X�N���[���̈ړ������Ɗ�����m�͂ǂ̂悤�ȊW�ɂȂ邩�B
�� �X�N���[������������Ɗ�����m��m�|1�ɂȂ�(L��l ��x��2x�ɂȂ邱�Ƃ���킩��)�B
�@������m�ł��C������ m�|1�ł�
������C
�@�@���������ł���Bm��2�� m��1�ɂȂ�̂�L��l�Cm��3��m��2�ɂȂ�̂�
�@L���Cm��4��m��3�ɂȂ�̂�L��
�ł���B������O���t�ɕ`���ƉE�}�̂悤�ɂȂ�B
(�Q) �P�X���b�g�ɂ���܁C����
�P�X���b�g�Ɍ��Ă�Ɖ�܌��ɂ�銱�͗l���ϑ������B���g�̏ꍇ�͒P�X���b�g�����܂��邱�Ƃ͂����Ă����͋N����Ȃ��B�Ȃ��C���̏ꍇ�͊��͗l�������̂��B
��d �̒P�X���b�g��Œ���������A�CB�CC�CD�CE�ł̌��̈ʑ�����/2������Ă���ꍇ�C�������͓��ʑ��ƍl������̂ŁCA��P�̌���B��P�̌��݂͌��ɑł����������B���l��C��D�̌���D��P�̌����݂��ɑł����������āCAB�Ԃ�BC�ԂɌ݂��Ɉʑ�������/2�̊W�̌��͑ł����������B����āCAP�|EP��m�� �̏ꍇ�ɃX�N���[�����P�_�͈Ð��ɂȂ�B���͐��g�ƈقȂ�C�X���b�g��ɓ_�������A�����Ă���ƍl������̂ŁC�P�X���b�g����̉�܌��ǂ�����������̂ŃX�N���[����Ɋ��͗l�����B�ł́C�������͂ǂ̂悤�Ȃ��̂ɂȂ邩�B�P�X���b�g�ƃX�N���[���܂ł̋�����l �Ƃ���(l �͏\���傫�����̂Ƃ���)�ƁC��L�̗��R�ɂ��C
�@�@AP�|EP����dtan����dsin����m�� ����
dsin����(2m�{1)�� ������ �ɂȂ�B(m��0�C1�C2�C3�C���) (15-4)
�����ɔ��F����p����Ɗe������m���Ƃɉ�܃X�y�N�g���������B�����ɑ��ĊO�����ԁC���������ɂȂ�悤���z���邪�C���i����(����0�Cm��0)�ł͖��邭�Ȃ邾���ŐF�͌����Ȃ��B
���̌��ʂƃ����O�̎������r���Ă݂�ƁC�`���I�ɂ͖��Â��t�ł���B�܂胄���O�̎����ł���m�� �����������C�P�X���b�g�̏ꍇ�͂��ꂪ�Ð������ł���B�܂��Cd �������O�̎����ł͕��X�N���[���Ԋu�C�P�X���b�g�̏ꍇ�̓X���b�g���ł���B�����O�̎����ŃX�N���[����Ɍ���銱�Ȃ͏�L�@(c)�ŋL�����悤�ɁC���X�N���[�����\������X���b�g�̕��ɂ�銱�͗l�ƕ��X���b�g��
��銱�͗l������邪�C���X���b�g���\������X���b�g�̕��́C���X���b�g�̊Ԋu��菬��������C���X���b�g���\������X���b�g�ɂ�銱�Ȃ̊Ԋu�̕����傫��(��L�@�Q�l)�B
�ڂ����v�Z�ɂ�������0 �̃X�N���[����̋��xI0����ƁC��܊p�� �ł̋��xI (��)��
I (��)���ł���C�E�}�̂悤�ȕ��z�ɂȂ�B
�s���z�[���ɂ���ܑ�
�j�ŏ����Ȍ����J�����ă����Y���g���ďW�����Ċώ@����ƉE�}�̂悤�ȓ��S�~�̖��Â������B����̓s���z�[���ɂ���܌��������Ăł������͗l�ł���B�s���z�[���J�����Ə̂���C�Ô��Ɍ����J����ƃX�N���[���ɂ����锠�̈�ʂɑ����ʂ邪�C���ƃX�N���[���̋���������l�̂Ƃ��ɂ͂�����Ƒ������邱�Ƃ��ł���B�����Y���Ȃ��̂ɂȂ����̂悤�ɂ��Ƃ��N����̂��B
�s���z�[���̔��aa ���������Ƃ��C��P�Ê���ܑ��Ƃ��Ă����̂ŁC
�@�@�@�@AP�|BP���CAP��
�@�@�@�@BP��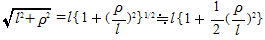
�� AP�|BP���@�@�@����� �ρ�
�s���z�[���̔��aa ���������Ɖ�܈Ê��傫���Ȃ邱�Ƃ��킩�邪�C����̓J�����́u�i��v�ɊW���Ă���B�܂�C�i��l��傫������Ɖ�܂ɂ��u�{�P�v�������ł��Ȃ��Ȃ邪�C�i��l������������ƁC�u���U�v�ɂ���ďœ_�[�x�̐�(�s���g�̍����Ă���͈͂������C�V���[�v�łȂ�)�ʐ^�ɂȂ�B�l�Ԃ̊�Ȃǂ��\�t�g�ɂƂ�Ƃ��ɂ͂��̕��������ꍇ������B
�����L���@�̏ꍇ�����l�ł���B�ŋ߂́C�����V���b�^�[�����������̃J�����ł͂��̂悤�ȋZ�͕K�v�Ȃ��̂����B
�����O�̎����Ɏ������������u(�����O�[��)
(a) �t���l���̋�
�Q���̋����p�x�� ���Ȃ��Đڍ����C�E�}��S�ɓ_������u���B���ꂼ��̋�����̔��ˌ��̌�_����S1�CS2����������̌���(�����O�̎����̕��X���b�g�ƌ��Ȃ���)�ƌ��Ȃ���B���̌��ʉE���̃X�N���[����Ɋ��Ȃ������̂�
d��S1S2��2btan����2b��
�� ��x��
(b)�t���l���̃o�C(��)�v���Y��
���p���������v���Y���Q���E�}�̂悤�ɐڍ������v���Y���Ɍ���S������𑗂�Ƌ��܌���S1�CS2�������O�̎����̕��X���b�g�̈ʒu�ɑ������X�N���[����Ɋ��Ȃ������B
����(n�|1)�������� (���ˁC���܂Ɋւ��鏔���ۇD�Q��)
d��S1S2��2btan����2b����2b (n�|1)��
�� ��x��
(c) ���C�h�̋� (H.Lloyd 1834�N)
���ʋ����ꂷ��Ɍ���S1����������˂�����ƁA��������̌���S2����o�Ă���悤�ɔ��˂��ăX�N���[�����bc�Ɋ��Ȃ����B���ʋ��ł̔��˂ł͈ʑ��������B
�����O�̎�����d ��2a�ɑ�������̂�
�@ ��x���ɂ���Ĕg���𑪒肷�邱�Ƃ��ł���B
���ʋ� �Ɠ���ʓ��̃X�N���[����̓_�ɁA�����O�̎����ł́u0���v�̊��͌����Ȃ��B
(�R)��܊i�q(grating)
�����O�̎����ł͕��X���b�g�͂Q�����ł��������C�X���b�g�Ԋu�ɐ��S�{�`����{�ȏ���ׂč��ꂽ���̂���܊i�q�ł���B���ߌ^�Ɣ��ˌ^�����邪�C���ߌ^�͌��w�I�ɖ����ꂽ�K���X�̕\�ʂɓ��Ԋu�ɏ���t���C���̂��ĂȂ���������̉�܌��̊��𗘗p������̂ł���B����C���ˌ^�͕����ȕ\�ʂɓ��Ԋu�ɏ������āC���ˌ��̊��𗘗p������̂ł���BCD�̕\�ʂɌ��Ă�ƐF�����Č����邪�C���ꂪ���ˌ^��܊i�q�Ɠ����̂��̂ł���CCD�ɂ���ꂽ�a�̊Ԋu�𑪒肷�邱�Ƃ��ł���B
���ߌ^��܊i�q�ŁC�i�q�萔d (�i�q�Ԋu��d)�̉�܊i�q�́C�i�q�ʂɑ���p�x�� �����̉�܌��ɂ�銱�������ߍ��������́C�ׂ荇�������̌��H���͏\�������ōl����� dsin��������
�@ dsin����m�� (m��0�C�}1�C�}2�C�}3��� )�ł���B (15-5)
��܊i�q�́C�����O�̎����ɔ�ׂăX���b�g����������̂ŁC�������N���Ɍ����(�E��ʐ^)�B
���}����܊i�q�̑���̕��@�ł���B��ɑ�(m��0)���獶�E��m��1�ł̋���x1�Cm��2�ł̋���x2�𑪒肷��B�p�x���������͈͂ł͂��ꂼ��̉�܊p�� ��
sin����tan���ƌ��Ȃ���̂ŁCm��1�ɂ��Ă�����d sin��1��d tan��1��
����g���𑪒肷�邱�Ƃ��ł���B���F�������g������ ��x �͔�Ⴗ��̂œ��ꊱ�����ł͊O�����ԁC���������F�ɂȂ�悤�ɕ��ԁB
�i�q�萔��d�C�i�q����m�Ƃ���ƁC��܋��xI �́C����0�ł̋��x��I0�C��܊i�q�̌��Ԃ̕���a�Ƃ�����������C
�ł���B
��P�����̂��Ă��鍀�͕�a�̂P�{�̃X���b�g�̋��x�C��Q�����ɂ������͊Ԋud �̖����ɋ���m�{�̃X���b�g�ɂ�鋭�x�������B
(�S)��������
�V���{���ʂɐF��������C�J�̓��ɘH�ʂ̐����܂�ɏ���������������ƑN�₩�ȐF�����Č����邱�Ƃ��@����B����炪�Ȃ��N����̂����l���Ă݂邽�߂ɁC���ܗ������ꂼ�� 1�Cn�Cn2�̋�C�C���C�����}�̂悤�ɂ���ꍇ�̊��ׂ�B���̌�����d�Cn��n2�ł���B
��C������ɓ��ˊpi �œ��˂����Q����A�CE ���l����B�����`�͖��Ƃ̋��E�ʂŋ��܊p r�ŋ��܂�����C���̒�ʂb�Ŕ��˂��C���Ɛ��̋��E�c�ɒB������Ăы�C�����܂���B����C����E�͋��E�c�Ŕ��˂������`�Ɗ�����BABCD�CEDF�̂Q�����̌o�H���́CBC�ɒ�������D����̑���B1�CBC�̉�������D���牔���ɉ��낵�����Ƃ̌�_��B2�Ƃ����
B1C�{CD��B1C�{CB2��2dcosr�C���H����2ndcosr �ł���B
�����d��D�Ŕ��˂���Ƃ��Ɉʑ��������(n��1)(�u�g�̐����v�g�̈ʑ��ω��Q��)���C����A��C�ł̔��˂ł�n��n2�Ȃ̂ňʑ��ω��͂Ȃ��B
����āCF�Ō����Ƃ��̖��Ï����́C���ˌ��̈�������̈ʑ�������邱�Ƃɂ���
�@�@�@�@�@ ������(m��0�C�}1�C�}2�C�}3��� ) 2ndcosr ����ˊpi �ŕ\����
�ł���B
�@�@�@�@�@ ����(15-6)
���̌��ʁCn�Cd �����̏ꍇ�C�g���� ��cosr ����Ⴗ��̂Ŕ��F�����̏ꍇ�C�F�����Č����邱�Ƃ��킩��B
�@ ���Ï����͋��ܗ��̑召�W�ňʑ��ω����ς�薾�Ï������ς��B
���}�ł��ꂼ��̋��ܗ��� n1�Cn2�Cn3�Ƃ����
n1��n2��n3 �Ŕ��ˌ��̊��ł́C������̔��ˌ����ʑ�������邽��
2n2dcosr��m�� ����������
(n1��n2��n3�͂�������ʑ��ω����N����Ȃ��̂œ������ʂɂȂ�)
n1��n2��n3 �Ŕ��ˌ��̊��ł́Cn2����n3�ւ̔��˂ł݈̂ʑ��������̂�
2n2dcosr��m�� ��������
�A ���ߌ��ɂ�銱��
���}�ŏォ�������˂������Ō����ꍇ�̊��ł�
n1��n2��n3 �ł͍��ۂ̈ʒu�ł̔��˂�n2����n3�̏ꍇ�݈̂ʑ�������邩��
2n2dcosr��m�� ��������
n1��n2��n3 �ł͔��˂ŗ����Ƃ��ʑ�������邩��
2n2dcosr��m�� ����������
�܂�C���ˌ��Ɠ��ߌ��Ŗ��Ï������t�ɂȂ邱�Ƃ��킩��B
�B �����̌���d ���傫���Ȃ�ƁC���F�����ł��F������Ȃ��B�V���{���ʂɐF�����Č����邪����̔Z�x�𑝂₷�ƌ����Ȃ��Ȃ�ꍇ�������B
���R�P�F
�g����1�C��2(��1����2�Ƃ���)�̐ڋ߂��������l����B��1�̔g���̌���m���̊������Ă���Ƃ�����2�̔g���̌���m�{1�Ŋ����Č݂��ɑł����������ƁC
2ndcosr��m��1��(m�{1)��2 �� ��1�|��2��
d���傫����m���傫���Ȃ�̂ŁC��1�|��2���������Ȃ�ڋ߂����g���̌������������Ď�ߍ����̂œ��ʂȐF�������Ȃ��Ȃ�B
���R�Q�F
d���傫���Ƒ����̈ʑ��C�g���̑��d���ˌ��Ɠ��ˌ����d�Ȃ�̂ŐF�̓����������Ȃ��Ȃ�B
�C ���˖h�~��
�K���X�̕\�ʂɃK���X�̋��ܗ���菬����������h�z���邱�Ƃɂ��K���X�ւ̓��ˌ��ƃK���X��ʂł̔��ˌ��̊��ɂ�蔽�ˌ����ŏ��ɂ��邱�Ƃ��ł���B�����̋��ܗ���n1�Ƃ����(�K���X�̋��ܗ�n��1.50�Ƃ����n1��n�Ƃ���)���ˌ��͂Ƃ��Ɉʑ��������̂Ŗʂɐ����̏ꍇ
2d�����Ï����ł���Bd �̍ŏ��l��m��0������ d��
���˖h�~���Ƃ���Na3AlF6(�X����n1��1.38)��p�����
d��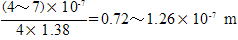
�g���ɂ����d ���قȂ邪�C���邭�����鉩�F�ɑ��Čv�Z����ƁC��F�ł��鎇�F�������Y�̕\�ʂɌ�����B���˂�h�~����ƁC���ߌ��������Ȃ�Ƃ������Ƃɂ���B���˖h�~���́C�J�����C�]�����Ȃǂɂ͕K���K�v�Ȃ��Ƃł���B���˖h�~���Ƃ��đ��ɂ�MgF2���p������B
�D ���ˌ��͉��F�Ɍ����邩
��L�̇@�̋��ܗ��̏�����n1��n2��n3 �ł���ꍇ(��C�|�K���X�|��C�̂悤�ȏꍇ)�ɁC�^�ォ�猩���ꍇ�ɔ��ˌ��̊��ɂ���ĉ��F�Ɍ����邩���l���Ă݂�B�������̔g���� �� ����4.0�`7.0�~10-7m�Cn2��1.4�Cd��4.0�~10-7m�Ƃ���ƁC
2n2d����������������C ����
�ł���B������m�ɑ���g�������߂��
2n2d��11.2�~10-7m������C�����A�Ƃ���
m��0�F A�~2��22.4�~10-7m �����Ȃ��C
m��1�F A�~(2/3)��7.47�~10-7m �����Ȃ��C
m��2�F A�~(2/5)��4.48�~10-7m �F
�܂�C���̏ꍇ�F�Ɍ����邱�Ƃ��킩��B�K���X�̌����ɂ���Č�����F���قȂ�̂ŁCm��0 �̏ꍇ�͈̔͂����߂�B
�㎮��m��0�Ƃ���� d����
��(0.714�`1.25)�~
m
�K���X�̌���d �� d��0.714�~10�|7�C d��1.25�~10�|7m�ł͓���̐F������Ȃ����Ƃ��킩��B
�E �j���ɐ�������ĉ����ɂ��Č���ƁC���ɍs���قǐF�̊Ԋu���Ȃ������Ȃ�̂��B
���̌�����d�C���ܗ���n�C���܊p��r1�Cr2�Ƃ���B���������͇D�̏ꍇ�Ɠ����ɂȂ邩��
�g����1�� 2ndcosr1���C�g����2��2ndcosr2��
�������� cosr1�|cosr2��
����āCd ���傫���� cosr1�|cosr2���������Ȃ�B�܂�ȊԊu���������Ȃ邱�ƂɂȂ�B
���͉��ɂ����قnj����Ȃ�B����Ȃǂ̔Z�x�ɂ���Ă��̌����͈قȂ邪���悻1�`10�~m�ł���B
�@�܂��C�オ���C�����ԂɂȂ�悤�ȐF�т��ł��Ă���l�q���킩�邪�C����͑�ꎮ����(�����͈͂�d �����ƍl�����)����cosr ����Ⴗ��̂Ŕg���̒����Ԃ̏ꍇr ���ł��������ƍl�����邪�C���U(�g���ɂ���ċ��ܗ�n���قȂ�B15-4�X�y�N�g���Q��)���W���Ă���̂ł��̗v�f���l�����Ȃ���Ȃ�Ȃ��B
�i�T�j��������
���w�I�ɖ����ꂽ�Q���̃K���X���d�ˁC�Е������ɔ������Ȃǂ����ނƏ��������X�����ł���B����ɏォ�甒�F�������˂��āC���ˑ����猩��Ɗ��͗l���ϑ��ł���(�E�ʐ^�Q��)�B������������тƌĂԂ��Ƃ�����B
�Q���̃K���X����C���ɒu����Ă���ꍇ���l����B��̃K���X�̉���Q�Ŕ��˂������ƁC���̃K���X�̏�ʂŔ��˂�����(�ʑ��������)�������ォ�猩��Ɗ��͗l��������B�Q���̃K���X�̋��ފp�x����(��0)�C0P��x�Ƃ���ƁC���}���
y/x��d/l��tan������(rad)
�Q�����̌��H���� 2(xtan��)��2x�� �CP�ł̔��ˌ��������ʑ��ω����邩��C
�@��m�� ���� �� x��
�@�@�@�@�@�@�@ �������@�@ �@�@�@��
(15-7)
���ȊԊu�ׂ͗荇�� m��m+1 ��x �̍�������
xm+1���~(m+1)���Cxm��
�~m�� �� ��x��xm+1�|xm��
����
(���Ԋu)
�K���X�Ԃɋ��ܗ�n �̕����������ꍇ������/n�ƒu�������āC��
�ł���B���̏ꍇ�Cn ���K���X�̋��ܗ�����ł�Q�_�ŁC���̏ꍇ��P�ł����ʑ�������邾���ŁC����������ʑ��ω�����_�͏�L�ƕς��Ȃ��̂Ŗ��Ï����͕ς��Ȃ��B
�@ �܂��C�ォ�������˂��C�����猩���ꍇ�́CP�Ŕ���Q�Ŕ��˂̂Q�˂�������Q����̋��܌��̊�������C���ˌ��̏ꍇ�Ɩ��Ï������t�ɂȂ�B
�������тɊ��͗l�������邱�ƂƓ��l�ɂ��āC�ꖇ�̃K���X��Ð��ʂɕ��s�ɂ��Ă킸���ȊԊu�Œu���C������˂���Ɗ��͗l�������B�K���X�����R�Ȃ犱�Ȃ͓��Ԋu�����C�����łȂ��ꍇ���Ԋu�ɂȂ炸�䂪�݂������̂ŁC�K���X�\�ʂ��ꍇ�̓_���ɗp���邱�Ƃ��ł���B�K���X��ʂƐ��ʂƂ̌��Ԃ��������т̃K���X�̌��ԂƓ����ł���B
�i�U�j �j���[�g�������O(Newton ring)
�}�̂悤�ɁC���K���X��ɋȗ����a�̑傫�����ʃ����Y��u���A���������𑗂�ƁA���̊��ɂ���ĐڐG�_�𒆐S�Ƃ��Č���铯�S�~��̎Ȃ��j���[�g�������O�Ƃ����B���K���X��̏��Q�ƕ��ʃ����Y����P�̔��ˌ��̊��ɂ����̂ł���B
�@���ʃ����Y�̋ȗ����a��R�Cd�Cr (���ʃ����Y�ƕ��K���X�̐ړ_����̔��a) ��}�̒����Ƃ���ƁC�Q�����̌o�H���́C�}����
d��R�|��
�o�H����2d���ŁC�Q�����̌o�H�͋�C�w������C���H���������B
���K���X��ł̔��˂����ʑ�������邩��
�@�@��������
(m��0�C�}1�C�}2�C�}3��� )
�@ �����@��m�� (15-8)
�@ ���ꊱ����m�ł́Cr �͖�����r��������
�@�@�g���� ���������Ԃ͊O���C���͓����ɂȂ�Bm��0��r��0 �����璆�S�͈Ð��ł���B(�E�O���t)
�A ���ߌ��ɂ�銱�ł́C���܌���Q�Ŕ��˂�(�����ňʑ��������)���ʃ����Y���ʂłӂ����є���
(�����ňʑ��������)�������̊��Ȃ̂Ŗ��Â̏��������ˌ��̏ꍇ�Ƌt�ɂȂ�B�܂蓯�S�~�̒��S�͖����ł���B
�B �K���X�Ԃɋ��ܗ�n �̕��������ƁC�g������/n�ɂȂ邩��C
r ' ���ł���B
�@ ���Ï����͕ς��Ȃ��B
�C ������m���P�قȂ�C���ׂ荇����(��)���ň͂܂ꂽ�h�[�i�c��̖ʐς�
��(rm+12�|rm2)����R�� ���B
�@ �܂�������O�����ʐς͕ς��Ȃ��B
�D ���F���̏ꍇr���傫���Ȃ�(�O��)�ƐF���������Ȃ��B����͔�������d���傫���ꍇ(�u4 �������v�B)�Ɠ����ł���B�P�F���̏ꍇ�͉E��̎ʐ^�ł킩��悤��r���傫���Ȃ��Ă����Ȃ͑N���Ɍ����B
�j���[�g�������O�̎�������C���ʃ����Y�̋ȗ����aR�C���̔g�����C�K���X�Ԃɓ��ꂽ�����̋��ܗ��Ȃǂ𑪒肷�邱�Ƃ��ł���B
�P�T�|�R ���͉��g(transverse wave)
���������O�̎����ȂǂŔg�ł��邱�Ƃ��킩�������C���g�ł��邱�Ƃ́C���}�̂悤�ɂQ���̕Ό��`�C�a��ʂ��ď�}�ł͌����������C���}�ł͕Ό��a��������ƌ����錻�ۂɂ���Ċm���߂���B
�d�C��(Mg3Al6B3Si6O27(OH�CF)4�B�O�����n)�ȂǂɎ��R������˂���ƁC���������Ɍ������z�������������C����ɐ��������͋z��������ɂȂ�̂ŁC������̐U�����������������܂��Ό��ɂȂ�B���̌�������ɂ����ꖇ���������������̓d�C��u���ƌ��͓��߂ł��Ȃ��Ȃ�B
�Ό��͓���̐U���ʂ̌������ʂ��Ȃ��B�Ό����C���߂�����ʂ����낦��Ɠ��߂��C����������Ɠ��߂��Ȃ����Ƃ����̗��R�ł���B�Ό��Ƃ́C ����̕��������U��������C����ь��ۂ������B

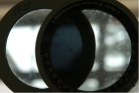
�Ό��ʂ��������Ȃ̂Ō������Ă��镔���Ɍ��͓��߂��� �Ό��ʂ��������Ă���̂Ō��͓��߂����Â��Ȃ�
���R���̕Ό��@
�@ ���˖@
���ˌ��͕Ό��ɂȂ邪�Cn��taniB�̂Ƃ��Ɋ��S�Ό��ɂȂ�B������u�����[�X�^�[�̖@���Ƃ����B
���}�ɂ����Č������������˂��C���ˁC���܂���B
���ܗ�n���� sin
��cos
�� iB�{rB���̂Ƃ��Ɋ��S�Ό��ɂȂ�B (15-9)
�� n��1.5�̃K���X�̏ꍇ�C i��57߂Ŋ��S�Ό�
�A ������(����C�����C�X�C�d�C�ȂLjꎲ�����B�_��C�����ȂǓ���)
���������̏�ɒu���B��������ʂɕ��s�ɉ�]������ƁC��������d�Ɍ��������d�ɂȂ����肪���݂Ɍ����B
(�E�}�͎��ʂɈ����ꂽ�Q�{�̐����S�{�Ɍ����Ă���)�B��������(�≖�C�����Ȃ�)�ȊO�͌������ɋ��܂������͓�̕��ɕʂ��B���̌��ۂ��������ł���B
�ꎲ�����̏ꍇ�C������̓|�����C�h(�Ό���)����]���Ă������Ȃ����C�ُ�����͋��܂̖@�������藧���Ȃ������ŋ��ܗ����قȂ�B������̌������ʕΌ��ł���B�����܂��}�����X(E.L.Malus)�ɂ���Ē��ׂ�ꂽ�B
�����ł́C����Ƃ��Ɉُ�����ł���B
�F�Ό������ �z���̂悤�ɕΌ���ʂ����Ό��͈��̐F�������B����͏�����ƈُ�����̊��̌��ʂł���B
���e��������G�|�L�V�����C�K���X�C�Z�����C�h�ȂǂɁC�c(�Ђ���)��^���Ό���ʂ��Ă݂�Ɨ͊w�I�Ђ��݂������ł�����@�B
�ʐ^�̓G�|�L�V�������g������B��(�~�ւ��㉺�Ɉ���������)�C��(�_�����k)�C�E(���_�ɋȂ��c�݂�^����)


�ȉ~�Ό�����ȉ~�ʂɐ����ɐi�ތ��������B�����ɕ��s�ɐ����ꎲ�����ɐ����ɕ��ʕΌ��āC������C�ُ�����̊Ԃɔ̊O�ňʑ����������Ăł���B
�~�Ό�������ȉ~�Ό��ňʑ�������/2�ɂȂ�ꍇ�������B
�P�T�|�S �X�y�N�g��(spectrum)
���U������^�͔g���� �ɂ�炸�Cc��f�� �����藧�����̕����ł͔g���ɂ���Č������قȂ邽�߂ɋ��ܗ����قȂ錻�ہB
�@�@�@�@�@�@ ���U�ɂ���Ăł�����̑т��X�y�N�g���Ƃ����B�g���������قNj��܂͏������B �g���|���ܗ��̃O���t
�X�y�N�g���̎��
(1) �A���X�y�N�g�� �����̌ő̂�t�̂ɂ��B(�g���̘A���������̂ő��z���C���M�d���̔�������Ȃ�)
(2) (�P)���X�y�N�g�� �����̋C�́C�C�̂̕��d�ł̌��q�̔����ɂ��B
���F�� H He C
�܂��C�A���X�y�N�g���Ɛ��X�y�N�g�����d�˂��(���M�d���̑O�Ƀi�g���E���̉���u���ꍇ�Ȃ�)�C�A���X�y�N�g���ɈÐ��X�y�N�g�����d�Ȃ��Č����顂�����z���X�y�N�g���Ƃ����B�Ⴆ�CNa��D���ƘA���X�y�N�g�����d�˂��D������������������B�������͂ɗp������B���z���Ɍ����t���E���z�[�t�@�[����H�CHe�CNa�CMg�CCa�̋z���X�y�N�g���ł���B
�� ���U�C���܂ɂ���Č���錻�ۂł���B
�E���̎ʐ^�̓��́C����̏���ɕ�����������B����͏オ�ԁC�����͉����ԂɂȂ��Ă��邱�Ƃ��킩��B
���͋�C���̐��H�Ɍ������˂��C���H�ւ̋��܁C���˂����J��Ԃ���C���ɋ��܂��Č����錻�� �����C���܂����������U���F���ʂ��B���H���ł̔��˂̉�p�C�Ίp�����C���H�ւ̓��ˊp��i�C���� �p��r �Ƃ���ƁCp��1�̏ꍇ�͐}��������|2(2r�|i) �ƂȂ�B
�@�@�@ p��1�ł́C����2(i�|r)�{p(�|2r) �̊W������B���̋ɏ��l�ɑ���i�Cr ��i0�Cr0�Ƃ����
�@�@�@����2(i0�|r0)�{p(�|2r0)
�������C�J�H�̋��ܗ���n �Ƃ���
(15-10)
���̓���̐F������������̓����ƂȂ��p�x���������|���ŁC���(p��1)�ł́C�ԐF��42�24'�C���F��40�32'�C����(p��2)�ł͐ԐF��50�24'�C���F��53�34'�ł���B���ꂪ����ƕ����ŐF�̔z�قȂ闝�R�ł���(�z��̈Ⴂ�͉E�}�Q��)�B
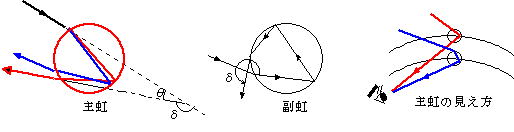
�������H�ɂ����̂ł��邱�Ƃ̓M���V�����ォ��m���Ă����B13���I�ɂ͋��܂ɂ����̍l�����Ă������C����C�����ɂ��Ă̓f�J���g��ɂ���Č�������Ă����B���̐F�����U�ɂ����̂Ǝ������̂��j���[�g���ŁC�u���w�v����L�̊p�x�� �ɂ��Ă��ӂ�Ă���B
�z�[�� ���j���[ �g�� �g�̐��� ���g �h�b�v���[���� ���U���C���U�� ���g�̏����� ���w
Top