ホーム  メニュー            熱と仕事   気体の法則  気体分子運動論    内部エネルギー    気体の状態変化  不可逆変化
                                                                             

１２−３ 気体分子運動

気体を構成する分子がどのような振る舞いをする結果として圧力を考えることができるのか。いくつかの仮定をおいてミクロの立場で分子運動を考える。
     仮定
　　1. 分子を質点とみなし，十分に乱雑に振る舞う。
　　2. 分子は弾性衝突する。つまり,運動エネルギー,運動量は保存される。
　　3. 分子は衝突時相互作用がある。
ここで，１辺の長さが l の立方体で体積がVの容器中に，質量mの気体分子がN 個ある場合を考える。
まず，１個の分子について考える。
  　右図のように器壁へ速度vで衝突すると，弾性衝突するからv_xは−v_xになるが，v_y，v_zは変わらない。
  　この分子の衝突前の運動量はmv_x，衝突後は−mv_xだから，１回の衝突での運動量変化は��p_x＝−2mv_x
  　分子が同じ壁に衝突するまでの時間は[s]だからt [s]の間の衝突回数は
  　よって，分子がt [s]間に壁から受ける力積f t は f t＝
  　壁が１個の分子から受ける力f は である。 (12-3-1)
物体の運動量の変化は，物体に加えられた力積に等しい。(「力学」−11-1運動量参照のこと)

N 個の分子について
　 壁が受ける全合力はすべての分子による力の和である。この全合力を面積A＝l² で割ると，
    壁に作用する全圧力として
　　　  (，，･･･はそれぞれの分子の速度のx 方向成分)
　　 の平均値は ，V＝ だから
                  (12-3-2)
　　1分子の速さの２乗は v²＝v_x²＋v_y²＋v_z²であり，分子が十分乱雑に運動するから，，は等しい。
　　よって  ＝＝＝  したがって，(12-3-2)は
　　　　　    (12-3-3)
　　この式から，圧力Pは分子の平均運動エネルギーに比例することがわかる。また，(12-3-3)を
　　　　　
　　と書き換える。が一定ならボイルの法則が成り立っていることを示す。
    温度Tはに関係していることを示している。

気体分子運動論は，ｸﾗｼﾞｳｽ，ベルヌーイ，ﾏｯｸｽｳｴﾙ，ﾎﾞﾙﾂﾏﾝらによって考えられた。

 １２−４ 分子の平均運動エネルギーと絶対温度

(12-3-3)式を理想気体1molについて適用すると(1molの体積をV，分子数N_Aアボガドロ数)
             (12-3-4)
 　　　理想気体では，気体分子の平均運動エネルギーは絶対温度に比例する
１分子当たりの平均運動エネルギーがであり，だからである。
この式からx方向の１分子当たりの平均運動エネルギーはである。y，z方向も同様に考えることができる。
これを一般化したものがエネルギー等分配則である。
　　　熱平衡にある系のエネルギーはすべての自由度に等しく分配される
つまり，単原子分子の平均運動エネルギーは，2原子分子では である。
　　分子の２乗平均速度(root mean square speed)
　　(12-3-4)で分子量をMとすると，N_A・m＝M×10⁻³(Kg/mol)から
　　　　　

ボルツマン定数はボルツマンが命名したのでなく，M.Plank(プランク定数で知られている)による
自由度とは，系の運動や状態変化を決める物理量のうち，互いに任意に変化しうる座標系の数。単原子分子では3，2原子分子では5
エネルギー等分配の法則は，定積モル比熱が温度に依存していることなどから，古典論の範囲にだけ適応できる。
気体の速さの例
     気体 分子量 vrms(m/s)
     水素         2.02   1902
     ﾍﾘｳﾑ        4.0    1352
      水           18       637
      ﾈｵﾝ        20.1     603
      炭酸ｶﾞｽ   44       408

マクスウエル(J.C.Maxwell 1831-79)によると ，熱平衡状態にある気体分子の速度分布は，全分子をN，分子の質量をm，ﾎﾞﾙﾂﾏﾝ定数をk，絶対温度をT，速度vとv＋dvの範囲にある分子数の割合p(v)dvは
     p(v)dv＝
で与えられる。
この値が最大値になるときの速さv_Pは
   
平均の速さは
     ＝0.921
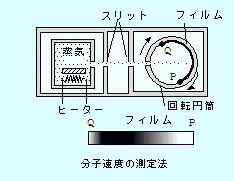
これらと，上記の２乗平均速度の大小はvp＜＜の関係にあるが分子の速度としてはを用いる。気体分子の速度は下左図装置のように回転円筒内に気体分子を送り込み，速度に応じてフィルムに写った濃さの違いから速度分布を計測することができる。温度によって速度分布が異なっている様子が下右図(測定例)のグラフからわかる。


                                          


平均自由行程(1860年Maxwellによる)
分子が他の分子に衝突せずに運動することのとできる平均の距離分子は平均して距離l 進んで1回他の分子に衝突する。半径r₀の分子を考える。
2つの分子の中心間距離がr₀より小さくなると衝突すると考える。右図の分子AにBは衝突せず，C，Dは衝突することになる。半径r₀内の円筒内に，平均して長さl 毎に他の分子の中心が1個含まれることになる。
分子密度をn(個／m³)とすると，
　　　　　πr₀l × n＝1       ∴   l＝
よって単位時間(1秒)毎の平均衝突回数は
　　　　　 (回／s)
平均衝突時間τは
         
( 実際は，他の分子も動いていることを考慮するとl＝，)

ホーム  メニュー            熱と仕事   気体の法則  気体分子運動論    内部エネルギー    気体の状態変化  不可逆変化
           Top