ホーム メニュー ![]() 熱と仕事 気体の法則 気体分子運動論 内部エネルギー 気体の状態変化 不可逆変化
熱と仕事 気体の法則 気体分子運動論 内部エネルギー 気体の状態変化 不可逆変化
12-5 気体の内部エネルギーとモル比熱
T(K) の理想気体1molの内部エネルギーUは,分子の運動エネルギーの和で与えられるので(12-3-4)式から
n[mol] ではこのn 倍だから
(12-5-1)
内部エネルギーは物質量,絶対温度に比例する
温度が⊿T [K] 変化した場合の内部エネルギー変化量⊿U は単原子分子では
→ Ne,Heなどの単原子分子1molでは⊿T=1で⊿U≒12[J]
2原子分子の場合は,
(⊿U の式の分子の3,5は自由度である。エネルギー分配の法則から,内部エネルギーは1自由度当たりずつ分配される。
「気体分子運動論」12-4自由度参照)
12-6 熱力学第1法則(first law of thermodynamics)
一般に,気体に外部から熱量Q[J]が加えられ,同時に仕事W[J]がされるとき,気体の内部エネルギーは増加する。このときの内部エネルギーの増加量を⊿Uとすると,
⊿U=Q+W (12-6-1)
の関係が成り立つ。これを熱力学第1法則という。
Q,Wの正負は,気体の内部エネルギーが増加する場合正,減少する場合負と考えればよい。
加熱の場合(気体は吸熱)Q>0,冷却の場合(気体は放熱)Q<0
圧縮ではW>0,収縮ではW<0
熱力学の第1法則はクラジウス(1822-88)による。
気体のする仕事W '
気体を加熱し気体が膨張できる場合,気体は外部に仕事をする。
この仕事W 'は右図のようにシリンダー内のピストンが自由に動ける場合,圧力が一定である。大気圧をPとすると,気体に熱をゆっくり与えると,気体の温度が上昇し,内部エネルギーが増加するので,ピストンを移動させてピストンに対して仕事をする。この仕事W 'は,移動量を⊿x,ピストンの断面積をSとすると,気体がピストンを押す力はF=PSで与えられるから,W '=F⊿x=PS⊿x=P⊿V (⊿V は体積変化で⊿V =S⊿x)。
W ' の正負は,気体が膨張する場合正,収縮する場合負である。グラフで考えると,PV グラフで右向き矢印の変化では正,左向き矢印の変化では負である。
W ' =P⊿V を使うと(12-6-1)式は
⊿U=Q+W ' =Q-P⊿V (12-6-2)
(12-6-1) 式のWは気体に外部から与えられる仕事。W ' は気体が外部(たとえばピストンに対して)にした仕事でW=-W '
気体が仕事をする(膨張する)と内部エネルギーが減少するので(12-6-2)になる。
気体のする仕事W 'はで与えられ,PV グラフの下側の面積に等しい。
熱力学第一法則の具体的例
① 体積を一定にして気体に熱の出入りのある場合
体積一定だからW =0 よって ⊿U=Q
気体を加熱Q >0 ∴ ⊿U> 0
(⊿U∝⊿T だから 温度上昇し内部エネルギーが増加する)
気体を冷却Q <0 ∴ ⊿U<0
(⊿U∝⊿T だから 温度下降し内部エネルギーが減少)
② Q=0 (断熱)として気体に外部から仕事Wの出入りがある場合
⊿U=Q+W から ⊿U=W
気体を圧縮すると W>0 ∴ ⊿U>0
(圧縮したことにより,分子の平均運動エネルギーが増加し温度上昇)
気体を膨張させると W<0 ∴ ⊿U<0
(膨張させたことにより,分子の平均運動エネルギーが減少し温度下降)
③ 気体に熱の出入りをさせ,気体が外部に仕事をする場合
気体を加熱すると Q >0 気体が膨張して外部に仕事をする。その大きさはP⊿V
⊿U=Q-P⊿V (P⊿Vは正だがその分内部エネルギーを減少させる)
気体を冷却すると Q <0 気体が収縮して外部に負の仕事をする。
⊿U=ー Q+P⊿V
気体のモル比熱
一般に、物質1molの温度を1K変化させるのに必要な熱量を物質のモル比熱という。気体の場合、気体が外部に対して仕事をすることができる場合があるので、体積が一定の場合の定積モル比熱と圧力が一定の場合の定圧モル比熱では値が異なる。
1molの気体にQ[J]の熱量を加えたとき、気体の温度が⊿T[K]上昇したとすると、この気体のモル比熱C[J/mol・K]は
(12-6-3)
定積モル比熱CV (定積変化(体積を一定にした状態変化)でのモル比熱定積の場合⊿V=0 だから
=12.5[J/mol・K](単原子分子の場合)
(2原子分子の場合)
定圧モル比熱(定圧変化(圧力一定での状態変化)でのモル比熱)
=20.8[J/mol・K] (単原子分子の場合)
(2原子分子の場合)
CP=CV+R をマイヤーの式という。
J.R.Mayer(1814-78) 熱の仕事当量を決定したことで知られる。12「熱とは」参照のこと
比熱比γ・・・ 定積モル比熱と定圧モル比熱の比を比熱比という。
気体のモル比熱 J/molK
CP CV
He 20.94 12.62
Ne 20.76 12.47
Ar 20.89 12.51
H2 28.85 20.53
O2 29.44 21.09
N2 29.17 20.82
(12-5-1)の内部エネルギーUはCVを使うと U = nCVT[J] (⊿U = nCV⊿T)
⊿Uは⊿T=0 の場合以外すべて ⊿U=nCV⊿T である
2原子分子の場合
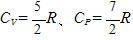
CV の分子の係数の3(単原子分子),5(2原子分子)はそれぞれの自由度である。
ホーム メニュー 熱と仕事 気体の法則 気体分子運動論 内部エネルギー 気体の状態変化 不可逆変化
Top